■問題PDF
令和6年度_学力検査問題過去問【埼玉】- 数学
■目次
大問1(小問集合)
大問2(関数)
大問3(平面図形)
大問4(総合問題)
■大問1(小問集合)
問題1-1: 5x-3x を計算しなさい。
解答 : 2x
解説 : 5x−3x=(5−3)x =2x 数字の部分を計算。 文字はそのまま。
問題1-2 : 2×(-4)-1 を計算しなさい。
解答 : -9
解説 : 2×(-4)-1=-8-1=-9 かけ算から計算。
問題1-3 : 6x²y×12y÷4x を計算しなさい。
解答 : 18xy²
解説 : 6x²y×12y÷4x=6x²×12y×1/4x=18xy²
わり算は分子と分母を入れ替えてかけ算にしてから計算する。
問題1-4 : 方程式 5x-7=6x-3 を解きなさい。
解答 : x=-4
解説 : xをイコールの左側、数字を右側に移動させる。
5x-6=-3+7 (5-6)x=4
-x=4 符号に注意する。
問題1-5 : √12+√3 を計算しなさい。
解答 : 3√3
解説 : √12 + √3 = √(3 × 2 × 2) + √3 = 2√3 + √3 = 3√3
問題1-6 : x²-x-72 を因数分解しなさい。
解答 : (x-9)(x+8)
解説 :x² – x – 72=(x – 9)(x + 8)
□ + △ = -1, □ × △ = -72, □ = -9, △ = 8,
問題1-7 : 連立方程式 { 6x – y = 10, 4x + 3y = -8 } を解きなさい。
解答 : x=1 y=-4
解説 : 連立方程式 { 6x – y = 10 …①, 4x + 3y = -8 …② } を解きなさい。
①の式に3を両辺にかける。
3(6x – y) = 10 × 318x – 3y = 30 …①’
①’ + ②より 22x = 22, x = 1
①の式に代入して 6 – y = 10
3y = -12
y = -4
問題1-8 : 2次方程式 2x² + 7x + 1 = 0 を解きなさい。
解答 : x=(-7±√41)/4
解説 : 解の公式より,
x = (-7 ± √(7² – 4 × 2 × 1)) / (2 × 2) = (-7 ± √(49 – 8)) / 4 = (-7 ± √41) / 4

問題1-9 : y が x の一次関数で、そのグラフの傾きが2で、点(-3, -2)を通るとき、この一次関数の式を求めなさい。
解答 : y=2x+4
解説 : 傾きが2なので、y = 2x + b
(-3, -2)を代入して -2 = 2 × -3 + b
-2 = -6 + b
b = 6 – 2 = 4
よって y = 2x + 4
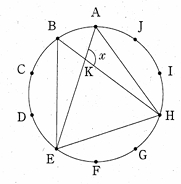
問題1-10 :図のように、円周の長さを10等分する点A~Jがあります。△AEHと△BEHをつくり、辺AEと辺BHとの交点をKとするとき、∠AKHの大きさを求めなさい。
解答 : 108 (度)
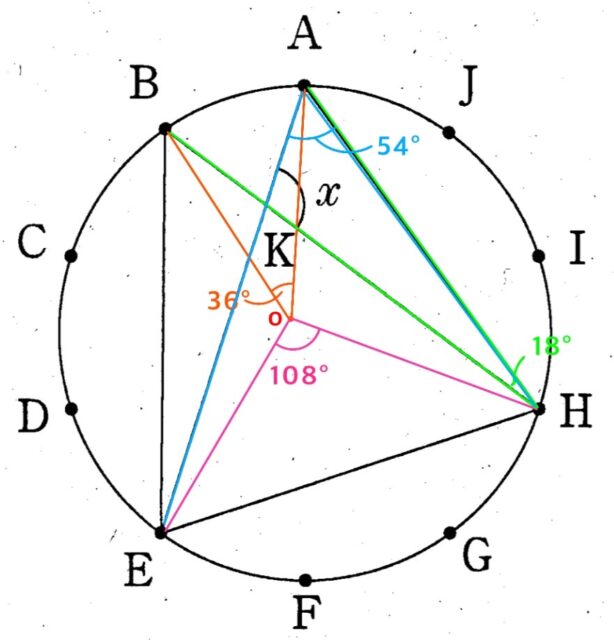
解説 : 中心Oをとると、中心角∠AOB = 360° × 1/10 = 36°
弧EHは弧ABの3倍なので、中心角∠EOH = 36° × 3 = 108°
∠AHK = 1/2
∠AOB = 1/2 × 36° = 18°
∠KEH = 1/2 ∠EOH = 1/2 × 108° = 54°
△AHKより、
∠x = 180° – (∠KEH + ∠AHK) = 180° – (54° + 18°) = 108°
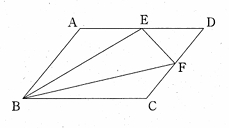
問題1-11 : 下の図のような平行四辺形ABCDがあり、辺AD, CDの中点をそれぞれE, Fとします。このとき、△EBFの面積は△DEFの面積の何倍になるか求めなさい。
解答 : 3 (倍)
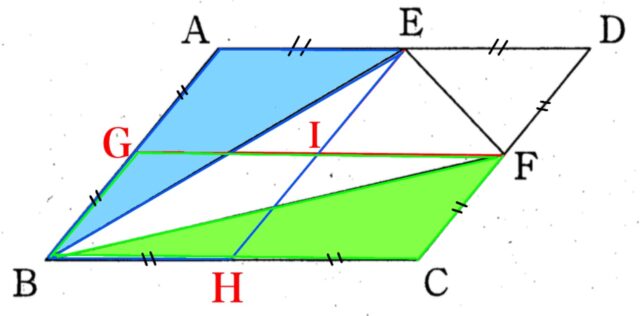
解説 : 平行四辺形ABCDの面積をSとする。対角線で4等分する。辺ABの中点をG、辺BCの中点をH、線分EHとGFの中点をIと置く。
△DEFは平行四辺形EIFDの面積の半分なので、△DEF = 1/2 × 平行四辺形EIFD = 1/2 × 1/4 S = 1/8 S
△ABEは平行四辺形ABHEの面積の半分なので、△ABE = 1/2 × 平行四辺形ABHE = 1/2 × 1/2 S = 1/4 S
△BCFも同様に、△BCF=1/2×1/2S=1/4S
△EBF = 平行四辺形ABCD – (△ABE + △BCF + △DEF) = S – (1/4 S + 1/4 S + 1/8 S) = 3/8 S
よって 3/8 S ÷ 1/8 S = 3
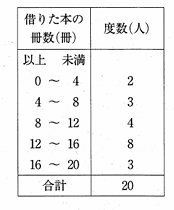
問題1-12 : 下の表は、あるクラスの生徒20人が、2学期に借りた本の冊数を、度数分布表に表したものです。この表から読みとることができる内容として正しいものを、次のア~エの中から一つ選び、その記号を書きなさい。
ア 中央値は8冊以上12冊未満の階級にある。
イ 8冊以上12冊未満の階級の相対度数は4である。
ウ 最頻値は8である。
エ 12冊以上16冊未満の階級の累積相対度数は0.85である。
解答 : エ
解説 :
ア: 全データが20人なので、中央値は、小さい方から10番目と11番目の平均となり中央値は12冊以上16冊未満の階級にある
イ: 相対度数は「その階級の度数」÷「全ての階級の度数の合計」で求めることができる。 4 ÷ 20 = 0.2
ウ: 最頻値とは、度数が最も大きい階級の階級値のこと。最も大きい度数は12冊以上16冊未満の階級なので、最頻値=12+16/2=14
エ: 累積相対度数は、「その階級の累積度数」÷「全ての階級の度数の合計」で求めることができる。累積相対度数は (2 + 3 + 4 + 8) / 20 = 17 / 20 = 0.85
問題1-13 : 1から6までの目が出る大小2つのさいころを1回投げて、大きいさいころの出た目の数をx、小さいさいころの出た目の数をyとします。このとき、10x + y が7の倍数になる確率を求めなさい。 ただし、大小2つのさいころは、どの目が出ることも同様に確からしいものとします。
解答 : 1/6
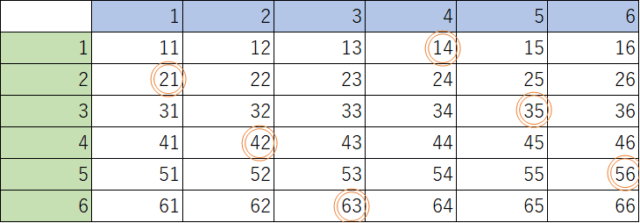
解説 : 表(図15)のように10x + y の値を書き出すと、7の倍数になるのは6通り。
さいころの出方は 6 × 6 = 36通りなので、確率は 6 / 36 = 1/6
問題1-14 : 下の図のような、AB = 6cm, BC = 4cm の長方形ABCDと直線lがあり、辺DCと直線lの距離は2cmです。このとき、長方形ABCDを、直線lを軸として1回転させてできる立体の体積を求めなさい。
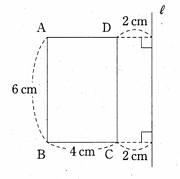
解答 : 192π (cm³)
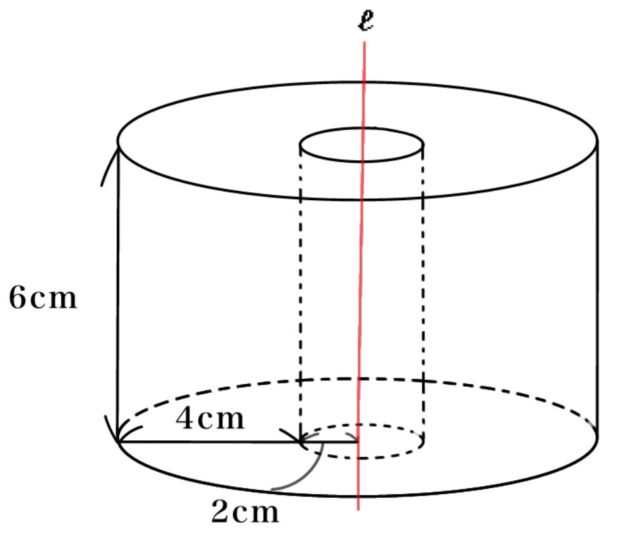
解説 : 求める面積は大きい円柱から小さい円柱を引いたもの(下図参照)。
大きい円柱: 6 × 6 × π × 6 = 216π cm³
小さい円柱: 2 × 2 × π × 6 = 24π cm³
よって求める面積は216π – 24π = 192π cm³
問題1-15 : 下の図のように、直線l上に1辺が8cmの正三角形を底辺が4cmずつ重なるようにかいていきます。正三角形をx個かいたとき、かげ(▲)をつけた重なる部分と重ならない部分の面積の比が2:5になりました。このとき、xの値を求めなさい。
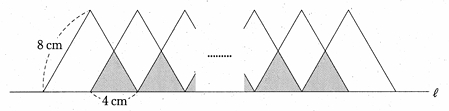
解答 : x=9
解説 : 重なる部分と重ならない部分の面積の比は、▲の個数と△の個数の比と等しい。
(例)
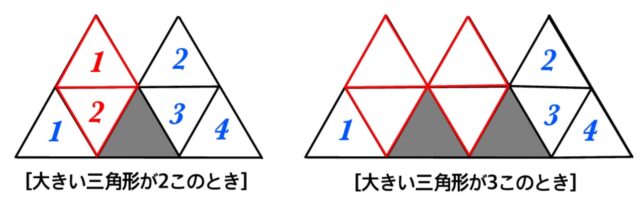
・大きい三角形が2このとき、▲=1こ、△=6こ。
・大きい三角形が3このとき、▲=2こ、△=8こ。
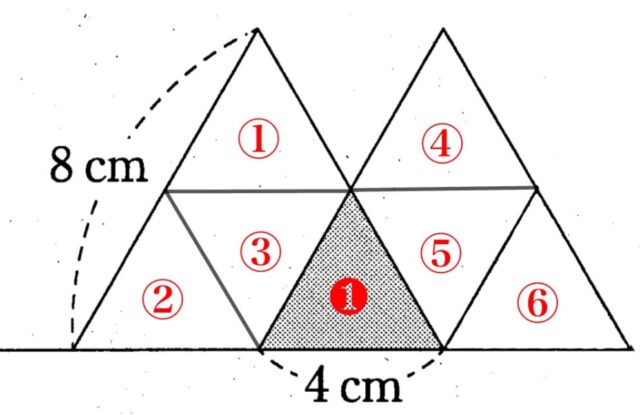
大きい三角形がxこのときは、▲は大きい三角形を1つ増やすごとに1こずつ増えるので、▲=x – 1こ、
△は左端の1こと右端の3こは同じで、▲×2の数ずつ増えるので、△= 2(x – 1) + 4 = 2x + 2こ,
(x – 1) : (2x + 2) = 2 : 5
5(x – 1) = 2(2x + 2)
5x – 5 = 4x + 4
x = 9
問題1-16 : 次は、先生とSさん、Tさんの会話です。これを読んで、下の問に答えなさい。
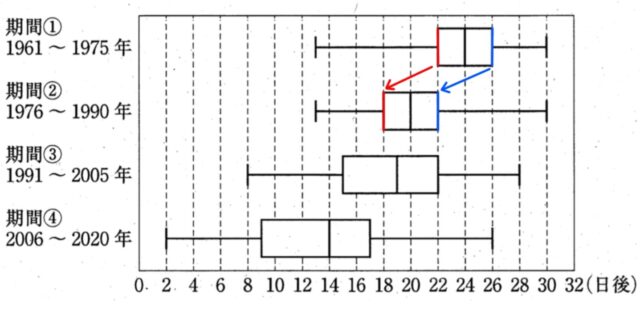
先生「わたしたちの中学校では、校庭にある桜の開花日を生徒会の役員が毎年記録しています。下の図は、1961年から2020年までの記録を、3月15日を基準日としてその何日後に開花したかを、期間①から期間④の15年ごとの期間に分け、箱ひげ図にそれぞれ表したものです。これを見て、気づいたことを話し合ってみましょう。」
Sさん「4つの箱ひげ図を見ると、桜の開花日は60年間でだんだん早くなっているようだね。」
Tさん「だけど、期間①と期間②の箱ひげ図は、最も早い開花日と最も遅い開花日が同じ位置だよ。それでも、開花日は早くなっているといえるのかな。」
Sさん「期間①と期間②の箱ひげ図を比べると、[ I ] から、期間①より期間②の方が、開花日は早くなっているといえると思うよ。」
問 会話中の[ I ]にあてはまる、開花日が早くなっていると考えられる理由を、第1四分位数, 第3四分位数という二つの語を使って説明しなさい。
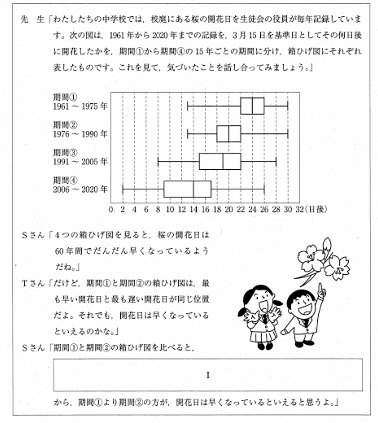
解答 : (説明)(例) 期間①より期間②の方が、第1四分位数, 第3四分位数ともに基準日に近い
解説 : 箱ひげ図より、第1四分位数は全体の25%、第二四分位数は全体の50%、第3四分位数は全体の75%の位置を示す。
期間①では、15年のうち7~8年程度は基準日の22~26日後に開花し、期間②では18~22日後に開花していたと分かる。
■大問2(関数)
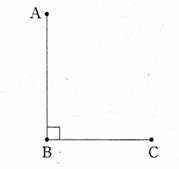
問題2-1: 下の図のように、∠ABC = 90° となる3点A、B、Cがあります。このとき、線分ACが対角線となり、AB // PC, AB : PC = 2 : 1 であるような台形ABCPの頂点Pをコンパスと定規を使って作図しなさい。 ただし、作図するためにかいた線は、消さないでおきなさい。
解答 : 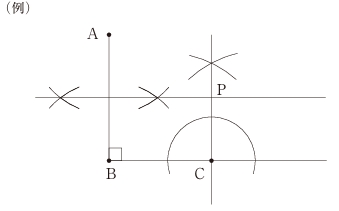
解説 :
手順1: 2点A, Bを中心に円弧を描く。
手順2: 交点2点を通るように直線を引く。
手順3: 点Cを中心に円弧を描く。
手順4: 直線BCとの交点に印をつける。
手順5: 手順4でつけた印を中心に円弧をかく。
手順6: 交点と点Cを通るように直線を引く。
手順7: 手順2と手順6の直線の交点が頂点Pとなる。
問題2-2: 下の図のように、直角三角形ABCの辺ABを1辺とする正方形ADEBと、辺ACを1辺とする正方形ACFGがあります。このとき、△ACD ≡ △AGB であることを証明しなさい。
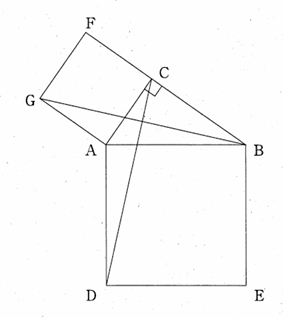
解答 : (証明)(例) △ACDと△AGBにおいて、
仮定から、AC=AG …① AD=AB …② ∠CAD=∠CAB+∠BAD =∠CAB+90° ∠GAB=∠GAC+∠CAB =90°+∠CAB …③
∠CAD=∠GAB …①.②.③から、2組の辺とその間の角がそれぞれ等しいので、
△ACD≡△AGB
解説 :証明と同様
■大問3(平面図形)
問題3-1: 次は、ある数学の【問題】について、先生とFさん、Gさんが会話している場面です。これを読んで、あとの各問に答えなさい。
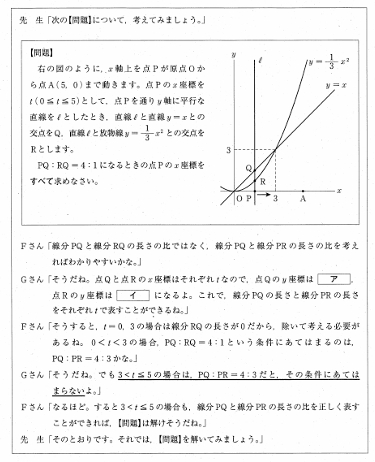
先生「次の【問題】について、考えてみましょう。」
【問題】 下の図のように、x軸上を点Pが原点Oから点A(5, 0)まで動きます。点Pのx座標を t (0 ≦ t ≦ 5) として、点Pを通りy軸に平行な直線をlとしたとき、直線lと直線 y = x との交点をQ、直線lと放物線 y = (1/3)x² との交点をRとします。 PQ : RQ = 4 : 1 となるときの点Pのx座標をすべて求めなさい。
Fさん「線分PQと線分RQの長さの比ではなく、線分PQと線分PRの長さの比を考えればわかりやすいかな。」
Gさん「そうだね。点Qと点Rのx座標はそれぞれ [ ア ]、[ イ ]になるよ。これで、線分PQの長さと線分PRの長さをそれぞれ t で表すことができるね。」
Fさん「そうすると、t = 0, 3 の場合は線分RQの長さが0だから、除いて考える必要があるね。0 < t < 3 の場合、PQ : RQ = 4 : 1 という条件にあてはまるのは、PQ : PR = 4 : 3 かな。」
Gさん「そうだね。でも 3 < t ≦ 5 の場合は、PQ : PR = 4 : 3 だと、その条件にあてはまらないよ。」
Fさん「なるほど。すると 3 < t ≦ 5 の場合も、線分PQと線分PRの長さの比を正しく表すことができれば、【問題】は解けそうだね。」
先生「そのとおりです。それでは、【問題】を解いてみましょう。」
[ ア ], [ イ ] にあてはまる式を、t を使って表しなさい。
解答 : ア:t イ:1/3 t²
解説 :点Qは直線y = x上なので x = t を代入
点Rは曲線y = 1/3 x² 上なので x = t を代入
問題3-2: 下線部の理由を、点Qと点Rのy座標にふれながら説明しなさい。
解答 : (説明)(例) 点Rの座標が、点Qのy座標より大きくなるから。
解説 :点Rは曲線y = 1/3 x² 上なので x = t を代入 大きくなるから。
つまり、線分PQより線分PRの方が長くなる。
PQ : RQ = 4 : 1 のとき、PQ : PR = 4 : 5 となる。
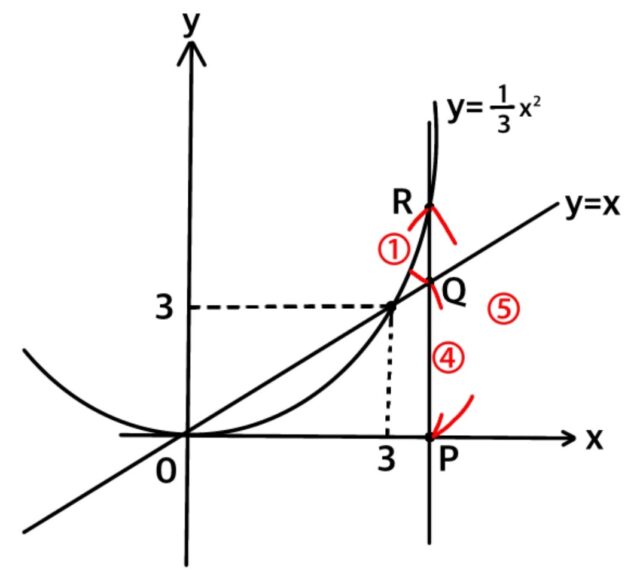
問題3-3: PQ : RQ = 4 : 1 となるときの点Pのx座標をすべて求めなさい。
解答 : x=9/4, 15/4
解説 :0 < t < 3 のとき PQ : PR = 4 : 3
t : 1/3 t² = 4 : 3 より t = 9/4
3 < t ≦ 5 のとき PQ : PR = 4 : 5
t : 1/3 t² = 4 : 5 より t = 15/4
■大問4(総合問題)
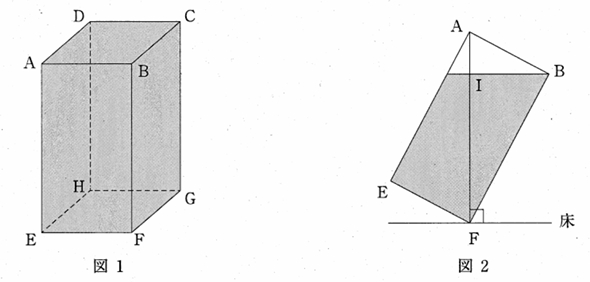
問題4-1: 図1のような、1辺の長さが6cmの正方形を底面とし、高さが12cmの透明でふたのない直方体の容器ABCD-EFGHを水で満たし、水平な床の上に置きました。辺FGを床につけたまま、図2のように、線分AFが床と垂直になるように容器を傾けて、水をこぼしました。水面と線分AFとの交点をIとするとき、次の各問に答えなさい。ただし、容器の厚さは考えないものとします。
容器に残っている水の体積を求めなさい。
解答 : 379 (cm³)
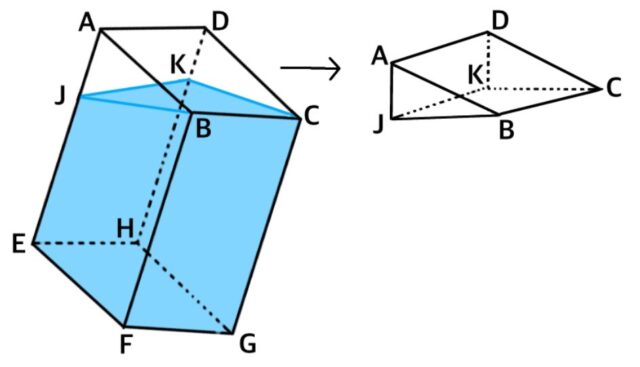
解説 :傾けたときの容器を立体で考える。
(図21)残っている水の量=四角柱の体積-三角柱の体積 ・四角柱の体積:6×6×12=432cm³,
・△三角柱の体積:直線BIとAE、DHとの交点をJ、Kとする。
∠AEF=∠BIA=90°、
∠AFE=∠BAIより△AEF∽△BIAとわかる。
△AEFにおいて、三平方の定理より(AF)²=12²+6²=180,AF=6√5cm
よって、EF:IA=AF:BA
6:IA=6√5:6
IA=6/√5cm
△BAJ∽△AEFより、BJ:AF=BA:AE
BJ:6√5=6:12
BJ=3√5cm
求める三角柱の体積は(3√5×6/√5×1/2)×6=54cm³
容器に残っている水の体積は 432 – 54√5 = 378 cm³
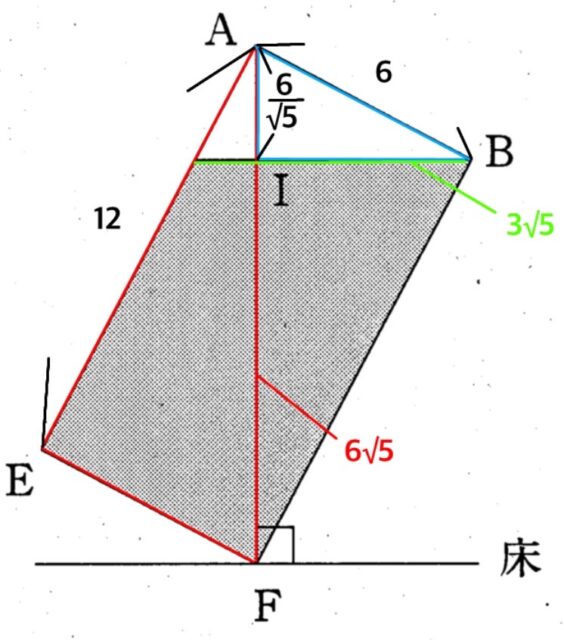
問題4-2: 床から水面までの高さFIを求めなさい。
解答 :24√5 / 5 (cm)
解説 :FI = AF – AI = 6√5 – 6/√5 = 24√5 / 5







