■問題PDF
令和7年度_学力検査問題過去問【千葉】- 数学
■目次
大問1
大問2
大問3
大問4
■大問1
問題1-1:次の①~③の計算をしなさい.
➀ 15 + (-7) × 3
解答 : -6
解説 : 掛け算を先に計算し, 足し算をする. (-7)×3=-21, 15+(-21)=-6
➁ (6a + 10b) ÷ 2 + 4a
解答 : 7a+5b
解説 : (6a+10b)を2で割り, 4aを加える. 3a+5b+4a=7a+5b
➂ (x + y)^2 – (x – y)^2
解答 : 4xy
解説 :展開すると, (x+y)^2 = x^2+2xy+y^2, (x-y)^2 = x^2-2xy+y^2, よって差は4xy
問題1-2:連続する3つの正の整数がある. 最も小さい数と最も大きい数の積から, 中央の数の2倍の数をひくと62になる。中央の数を x とするとき, 次の①, ②の問いに答えなさい。
➀ x についての方程式として最も適当なものを, 次のア~エのうちから1つ選び, 符号で答えなさい.
ア x^2 – 64 = 0
イ x^2 – 4x – 60 = 0
ウ x^2 – 2x – 63 = 0
エ x^2 + 16x + 64 = 0
解答 :ウ
解説 : 連続する3つの正の整数は, 中央の数を x とすると, (x-1), (x), (x+1) と表され, 最も小さい数と最も大きい数の積から, 中央の数の2倍の数をひく式は
(x-1)(x+1)-2(x) となり, これが62に等しいので, (x-1)(x+1)-2(x)=62, x^2-2x-1=62, x^2-2x-63=0
➁ 次の「あ」における答えを求めなさい. 中央の数 x は あ である。
解答 : 9
解説 :x^2-2x- 63の因数分解を考える. 積が-63で和が-2になる2つの数は -9 と 7であり, これを使って因数分解すると(x-9)(x+7) = 0.
方程式の解からx=9 (x=-7は x が正の整数であることに反しているため不適)
問題1-3:次の①, ②の問いに答えなさい.
➀ 次のア~エのうち, 正しくないものを1つ選び, 符号で答えなさい.
ア 5の平方根は √(5) と -√(5) である.
イ √(2) は循環しない無限小数である.
ウ 正の数 a, b について, a < b ならば √(a) < √(b) である.
エ √4は無理数である.
➀ 次のア~エのうち, 正しくないものを1つ選び, 符号で答えなさい.
ア 5の平方根は √(5) と -√(5) である.
イ √(2) は循環しない無限小数である.
ウ 正の数 a, b について, a < b ならば √(a) < √(b) である.
エ √4は無理数である.
解答 :エ
解説 : √(4) は無理数ではなく有理数(=2)

➁ 次の「い」「う」にてはまるものをそれぞれ答えなさい.
√(90n) の値が自然数となるような, もっとも小さい自然数 n は いう である
解答 :い=1, う=0
解説 : 90=2×3^2×5, 平方数にするためには2×5=10を掛ける必要がある
問題1-4:生徒32人に, 1問4点, 全部で5問の漢字テストを行った結果, 次のとおりになった. ただし, 1問に対する得点は, 0点または4点だけとする.
• 第1四分位数は8点
• 第2四分位数は12点
• 第3四分位数は14点
• 得点が16点の生徒は5人
➀ 32人の得点の四分位範囲は え である.
解答 :6
解説 : 第1四分位数 (Q1) は8点, 第3四分位数 (Q3) は14点. 四分位範囲はQ3−Q1=14

➁ 32人のうち, 得点が20点の生徒は お 人である.
解答 :3
解説 : テストの1問に対する得点は0点か4点. よって14点の生徒は存在せず, 第3四分位数 (75%) までの生徒の得点は12点となる.
よって並べ替えた得点の 24 番目 (テストを受けた生徒32人の75%) までが 12 点, 25~29 番目が 16 点 (5人) であるため, 残り 30~32 番目の 3 人が 20 点となる
問題1-5:下の図のように, AD=1 cm, AE=√(3) cm, EF=2 cm の直方体と, A, B, C, D, E, F, G, Hの文字が1つずつ書かれた8枚のカードがある. この8枚のカードをよくきって, 同時に2枚のカードをひく. ひいたカードに書かれた文字と直方体の頂点の文字は対応しているものとし, ひいたカードに書かれた2つの文字の頂点を結んでできる線分について考える. 例えば, AとBの文字が書かれたカードを同時にひいた場合は, 線分ABについて考える. このとき, 次の①の「か」「き」, ②の「く」「け」にあてはまるものをそれぞれ答えなさい. ただしどのカードを引くことも同様に確からしいものとする.
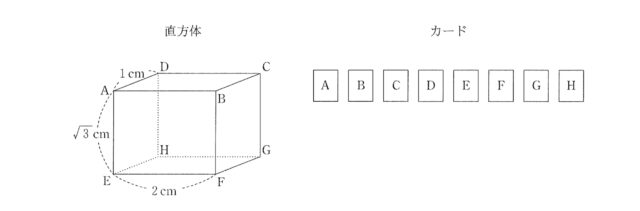
➀ ひいた2枚のカードに書かれた2つの文字の頂点を結んでできる線分の長さが2cmである確率は か / き である.

➀ ひいた2枚のカードに書かれた2つの文字の頂点を結んでできる線分の長さが2cmである確率は か / き である.
解答 :か=2, き=7
解説 : 長さ 2 cm の線分は 8 本, 全組合せは 28 通り
➁ ひいた2枚のカードに書かれた2つの文字の頂点を結んでできる線分の長さが2cmより長い確率は く / け である
解答 :く=3, け=7
解説 : 長さ 2 cm より長い線分は 12 本, 全組み合わせは28通り
問題1-6:3つの直線 3x+2y=7, 5x−4y=19, 2x+ay=11 が1点で交わるとき, 次の①の「こ」〜「し」, ②の「す」「せ」にあてはまるものをそれぞれ答えなさい.
➀ 3つの直線の交点の座標は( こ, さし)である
解答 :こ=3, さ= – , し=1
解説 : (1) 3x+2y=7 と (2) 5x−4y=19 を連立して計算
まず 3x+2y=7 を2倍にし, (1)’ 6x+4y=14 (2) 5x-4y=19 ・(1)’と(2)を足し算すると, 6x+4y + 5x-4y = 14+19, 11x=33, x=3となりこれを3x+2y=7 に代入, 3×3+2y=7, 9+2y=7, 2y=-2, y=-1. よって解答は x=3, y=-1
➁ a の値は すせ である く / け である
解答 :す= – , せ=5
解説 : 交点 (3, −1) を 2x + a y = 11 に代入して 6 − a = 11, a=5
問題1-7:下の図のように, △ABCがある. この△ABCを, 点Oを回転の中心として反時計回りに110°だけ回転移動させたものが△A’B’Cである. このとき, 次の①, ②の問いに答えなさい.
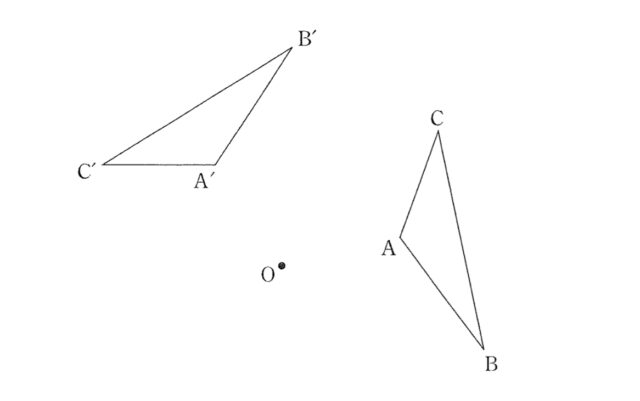
➀ 図の説明として正しくないものを, 次のア〜エのうちから1つ選び, 符号で答えなさい.
ア OA=OA’である.
イ 点Aが点A’まで移動した跡は, 直線である.
ウ ∠COC’=110°である.
エ ∠AOA’=∠BOB’ である.
解答 :イ
解説 : (“回転移動で点Aの軌跡は円弧. 直線にはならない.
ア 回転移動では, 回転の中心からの距離は変わらないため, OA=OA’となる.
ウ 回転移動ではすべての点が中心Oを基準に同じ角度で回転するため, ∠COC’も回転角度の110°と等しくなる.
エ 回転移動では, すべての点が同じ角度だけ回転するため, ∠AOA’=∠BOB’となる”
➁点Aを, 点Oを回転の中心として反時計回りに55°だけ回転移動させた点Pを作図しなさい. また, 点Pの位置を示す文字Pも書きなさい. ただし, 三角定規の角を利用して直線をひくことはしないものとし, 作図に用いた線は消さずに残しておくこと.
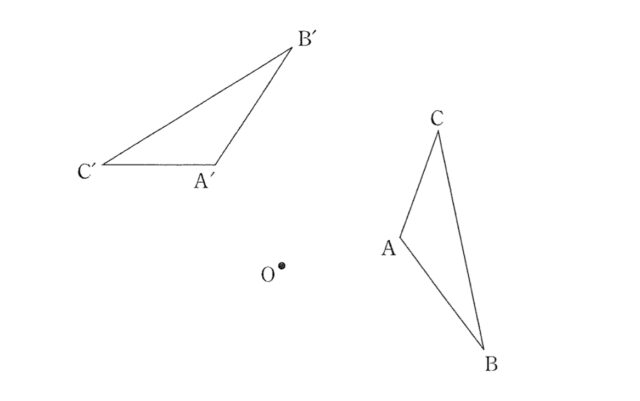
解答 :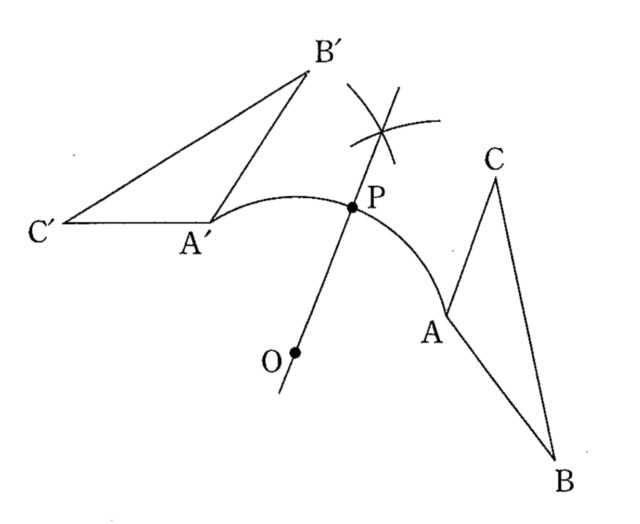
解説 : 中心 O, 半径 OA でAからA’まで円弧を描く
∠AOA’ = 110° の二等分線を作図する
二等分線と円弧の交点を P とする
■大問2
“下の図のように, 関数 y=ax^2のグラフ上に2点A, Bがあり, 点Aのx座標は-2, 点Bの座標は(6,9)である. このとき, 次の (1) 〜 (3) の問いに答えなさい.
ただし, 原点 O から点 (1, 0) までの距離及び原点 O から点 (0, 1) までの距離をそれぞれ 1 cm とする.
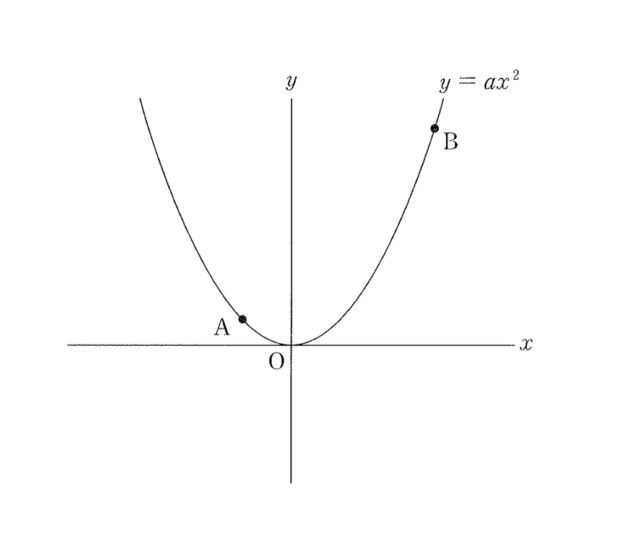 “
“
問題2-1:3次の「そ」「た」に当てはまるものをそれぞれ答えなさい. a= そ / た である.
解答 :そ=1, た=4
解説 : 点 B(6,9) が y=ax² を満たすので 9 = 36a, a = 1/4
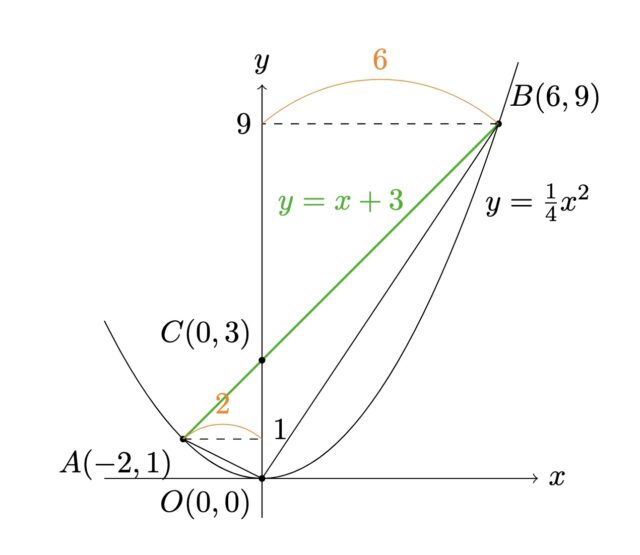
問題2-2:次の「ち」「つ」に当てはまるものをそれぞれ答えなさい. △OABの面積は ちつ cm^2 である.
解答 :ち=1, つ=2
解説 : “AB: y=x+3 (緑) とy軸との交点をC(0.3)とし△OACと△OBCに分けて面積を考える. それぞれの底辺は共通でOC=3. 高さはそれぞれA座標とB座標のx座標 (オレンジ) となり, △OAC=1/2(3×2)=3, △OBC=1/2(3×6)=9, よって△OABは12
問題2-3:”下の図のように, 直線AO上に点Cを, 関数 y=b / x のグラフ上に点Dを, 四角形ABCDが平行四辺形になるようにとる. ただし, 点Cのx座標は正, 点Dのx座標は負とし, b>0 とする. △OCDの面積が 24cm^2 のとき, b=てとである
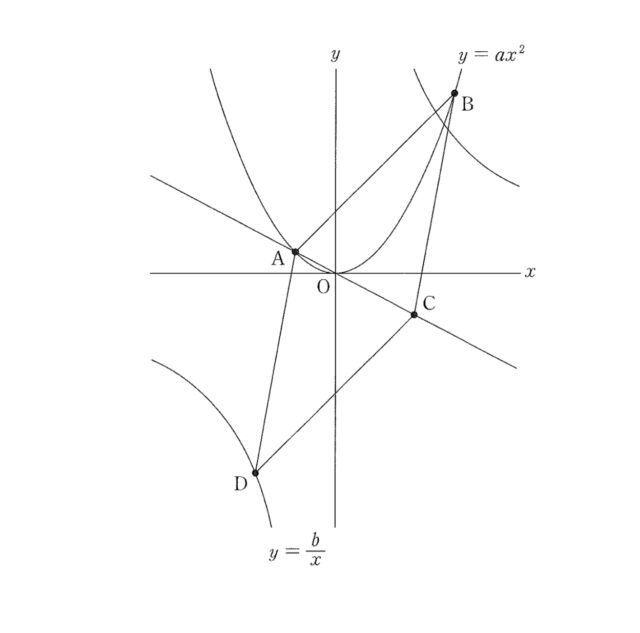

解答 :て=4, と=0
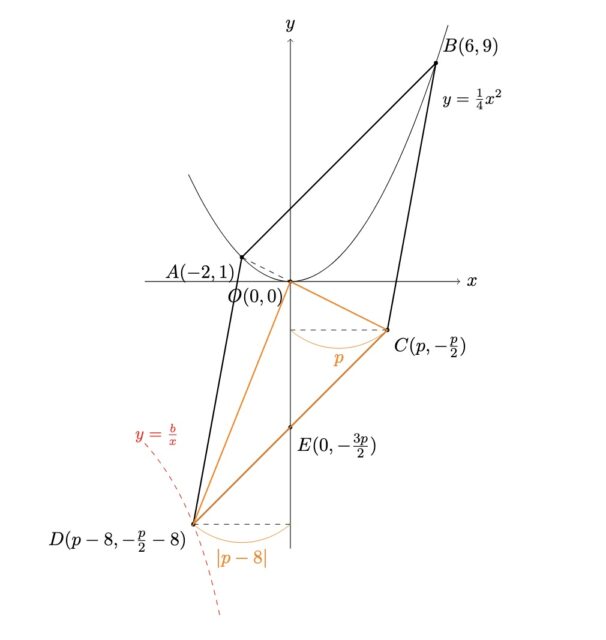
解説 : “直線 OA は y = -x/2. OA 上で x>0 の点を C(p, -p/2) とする. 平行四辺形にするためには AB=CD なので, D = (p−8, -p/2−8). よってDCはABと並行 (平行四辺形の対辺は並行) であることとCの座標より, DC : y=x-3p/2. DCとy軸交点をEとする. △OCE=1/2×3p/2×p, △ODE=1/2×3p/2×(-p+8). △OCD=△OCE+△ODE=6p. △OCDの面積は24より、p=4. したがってD(-4,-10). Dはy=b/x上の点より、-10=b/-4, b=40.
■大問3
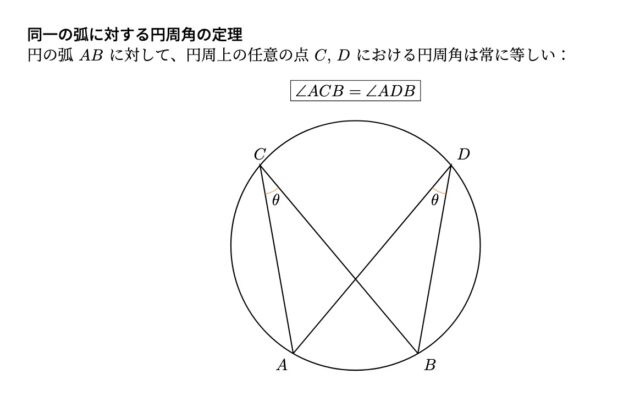
“”下の図のように, 線分ABを直径とする半円Oがある. 孤AB上に, ∠AOCが鋭角となるように点Cをとり, 線分BC上に2点B, Cとは異なる点Dをとる. 直線ADとABとの交点で, 点Aとは異なる点をEとし, 点Bと結ぶ. また, ∠AOCの二等分線と線分AE, ACとの交点をそれぞれF, Gとする. このとき, 次の (1) 〜 (3) の問いに答えなさい.
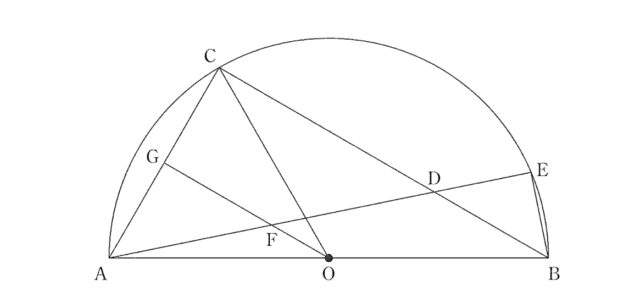
問題3-1:”次の (a), (b), (c) にはいるもっとも適当なものを, 選択肢のア〜カのうちからそれぞれ1つずつ選び, 符号で答えなさい.
線分OAと線分 (a) は, 半円Oの (b) だから長さが等しい. よって, △OCAは (c) である.
選択肢:ア OC, イ AB, ウ 直径, エ 半径, オ 二等辺三角形, カ 直角三角形”
解答 :(a)=ア, (b)=エ, (c)=オ
解説 : △OCAは OA=OC (円Oの半径) の二等辺三角形
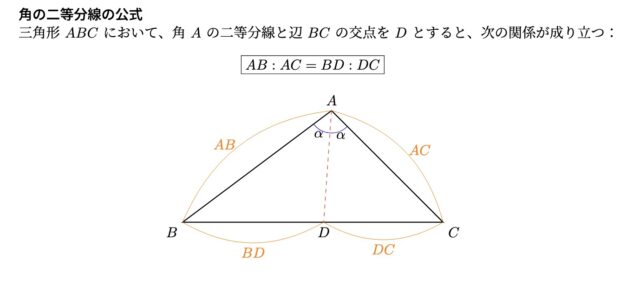
問題3-2:△AGF ∽ △EBD となることを証明しなさい. ただし, (1)のことがらについては, 用いてもかまわないものとする.
解答 :”△AGF と △EBD において, 二等辺三角形OCA の頂角の二等分線は, 底辺を垂直に2等分するから, ∠FGA=90 (①). 直径に対する円周角だから, ∠DEB=90 (②). ①, ②より, ∠FGA=∠DEB (③).
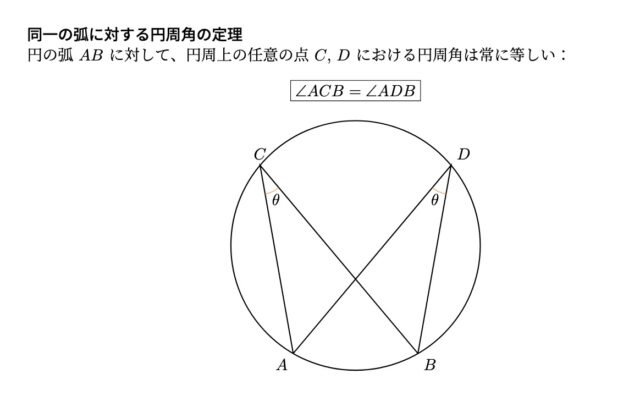
孤CEに対する円周角は等しいから, ∠GAF=∠EBD (④). ③, ④より, 2組の角がそれぞれ等しいので, △AGF∽△EBD”
解説 : “△AGF と △EBD において, 二等辺三角形OCA の頂角の二等分線は, 底辺を垂直に2等分するため, ∠FGA=90 (①). 直径に対する円周角より, ∠DEB=90 (②). ①, ②より, ∠FGA=∠DEB (③).
孤CEに対する円周角は等しく, ∠GAF=∠EBD (④). ③, ④より, 2角相当, △AGF∽△EBD
 “
“
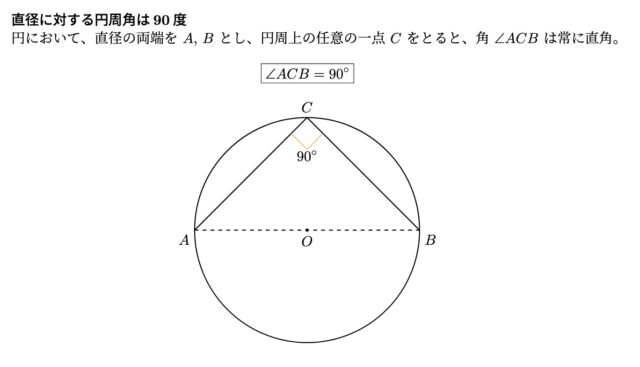
問題3-3:”次の「な」〜「ね」にあてはまるものをそれぞれ答えなさい.
OA=CA=6 cm, BD:DC=1:2であるとき, △EBDの面積は {(なに) √(ぬ)} / ね cm^2 である. “
解答 :な=1, に=2, ぬ=3, ね=7
解説 : “OA=CA=6, ∠ACB=90° (直径の円周角) より, △ABCで三平方の定理から BC^2=AB^2-AC^2=144-36=108, よってBC=6√(3).
BD : DC = 1 : 2 より, CD=4√(3), BD=2√(3). また, 同様に△ACDで三平方の定理より, AD^2=AC^2+CD^2=36+48=84, AD=2√(21). △ACDと△BEDは, ∠ACD=∠BED=90°(直径の円周角) , ∠CAD= ∠EBD (孤CEの円周角) により二角相等で相似. AD : BD = 2√(21) : 2√(3) より△ACDと△BEDの相似比は2√(21) : 2√(3). よって面積比はその2乗 84 : 12, 21 : 3. △ACD=1/2(AC×CD)=1/2{6×4√(3)}=12√(3), △BED=(3/21)△ACDより, △BED=(3/21)×12√(3)={12√(3)} / 7
■大問4
“次の会話文を読み, 会話文中の「の」〜「も」について, あとの (1) 〜 (6) の問いに答えなさい.
会話文
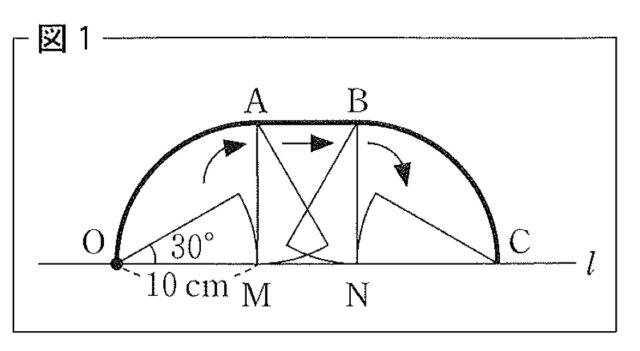
教師T:おうぎ形と円錐を, それぞれすべらないように転がしたときについて考えましょう. 図1の太線部分は, 半径OMが10cmで中心角が30度のおうぎ形を, 直線 l 上ですべらないように転がしたとき, 点Aが移動した跡を表しています. 点A, B, M, Nは, ∠OMA=∠ONB=90° となる点です. 点Cは, 直線 l 上にあり, おうぎ形を転がし終わった後の点Aの位置を表しています. このとき, 図1の点Oから点Cまでの太線部分の長さを求めてください.
生徒S:まず, 点Oから点Aまでの太線部分の長さは の πcmです. この長さと, 点Bから点Cまでの太線部分は同じ長さです.
教師T:そのとおりです.
生徒S:次に, 点Aから点Bまでの太線部分は, 直線 l からの距離が常に10cmとなるので線分になります. また, 直線 l 上ですべらないように転がしているので, 線分ABの長さはおうぎ形の弧の長さに等しいです. よって, 点Oから点Cまでの太線部分の長さは はひ / ふ πcmです.
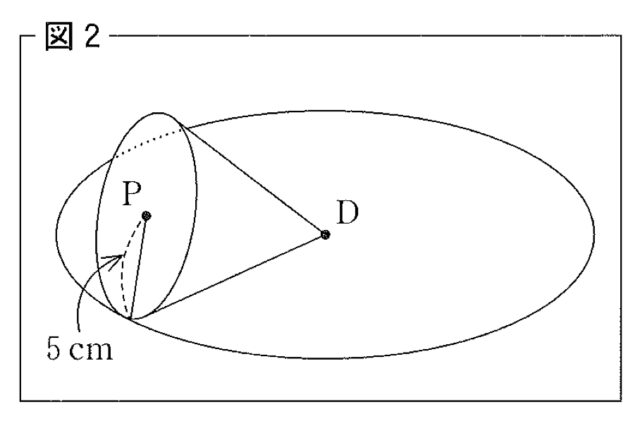
教師T:正解です. では, 次の問題です. 図2 のように, 頂点D, 半径5cmの円Pを底面とする円錐を, 点Dを中心として平面上ですべらないように転がしました.
このとき, 円Dの上を1周して, もとの位置にもどるまでに, 円錐はちょうど2回転しました. この円錐の母線の長さは何cmですか.
生徒S:円Pの周の長さと円Dの周の長さの関係から, 円錐の母線の長さは へほ cmです.
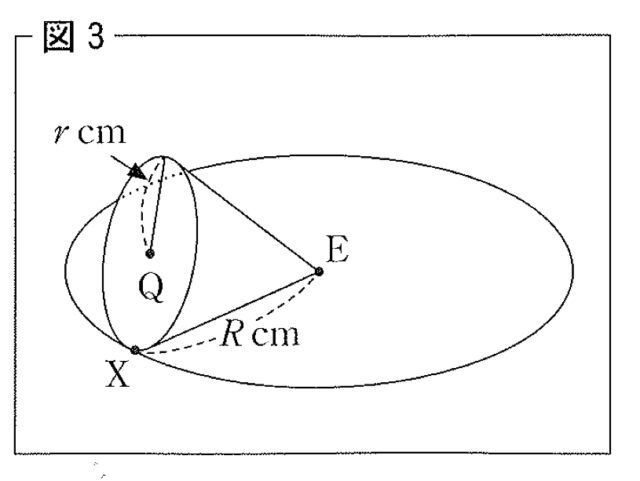
教師T:すばらしいです. また図3 のように, 頂点E, 底面が半径 r cmの円Qで, 母線の長さが R cmの円錐を, 点Eを中心として平面上ですべらないように転がしました. 点Xは, 円錐を転がす前の, 円Qが円Eに接している点を表しています. rとRの値を変えながら, 点Xの動きを考えてみましょう. 例えば, r=2, R=8とすると, 円錐の点Xは, 円錐がちょうど4回転したときに円Eの上を1周し, もとの位置に戻ります. しかし, r=9, R=24とすると, 円錐が何回か回転して円Eの上を1周したとき, 円錐の点Xはもとの位置にはありません. では, r=9, R=24のとき, 円錐の点Xが初めてもとの位置に戻るのは, 円錐が円Eの上を何周したときですか.
生徒S:円Eの上を ま 周したときに初めてもとの位置に戻ります.
教師T:正解です. さて, 図3 の円錐の点Xにインクをつけて, 点Xが初めてもとの位置に戻るまで円錐を転がしたところ, 点Xが接した円Eの周上に, インクの跡が残りました. r=2, R=8のとき, もとの位置を含めてインクの跡は全部で4個残りました. それでは, r=9, R=24のとき, インクの跡は全部で何個残りますか. ただし, インクの跡は点Xが接した円Eの周上に必ず点として残るものとします.
生徒S:もとの位置を含めて, インクの跡は全部で み 個残ります.
教師T:正解です. さらに r=9, R=24のとき, 円錐を転がす前の点Xの位置を点X_0として, 円錐を転がしたときにできたインクの跡を, 跡ができた順に, 点X_1, X_2, X_3, … とすると, ∠X_5 EX_6 の大きさは何度になりますか. ただし, 0度以上180度以下とします.
生徒S:むめも 度です. rとRの値を変えれば, 他にもおもしろい問題ができそうです.
問題4-1:「の」にあてはまるものを答えなさい
解答 :の=5
解説 : 90°の円弧の長さ= (90/360)×2π×10 = 5π
問題4-2:「は」〜「ふ」にあてはまるものをそれぞれ答えなさい
解答 :は=3, ひ=5, ふ=3
解説 : “AB=MNであり, MNはおうぎ形の弧の長さに等しく, MN=2π×10×30/360=5π/3=AB.
5π (OA) + 5π/3 (AB) + 5π (BC) = 35π/3″
問題4-3:「へ」「ほ」にあてはまるものをそれぞれ答えなさい
解答 :へ=1, ほ=0
解説 : 円錐が2回転して円Dを1周するため, 円錐の底面積の円周の2倍が円Dの円周. よって円Dの円周=2π×5×2=20π, 円Dの半径=20π×1/(2π)=10. 円錐の母線の長さは円Dの半径に等しく, 母線の長さは10cm
問題4-4:「ま」にあてはまるものを答えなさい
解答 :ま=3
解説 : “R/r=24/9で, 最小の周回数k (正の整数) は24k/9を整数にする最小のkより3
(24/9)×3=8″
問題4-5:「み」にあてはまるものを答えなさい
解答 :み=8
解説 : (4)より, 円E上を3周して初めて元の位置に戻るため, 3周分の長さは48π×3=144π. 円錐は1周回って18πより, 144π÷18π=8. 円錐の回転数がインクの跡の数と等しいため8
問題4-6:「む」〜「も」にあてはまるものをそれぞれ答えなさい
解答 :む=1, め=3, も=5
解説 : 円錐を1回転させると, 円Eの円周上では全体の3/8進む. すなわち, 角度で考えると(3/8)×360°=135°になる. よって1回の回転では135°進み, 5回転目から6回転目までの角度の変化は同じく135°







