■問題PDF
2025年度 兵庫県学力検査問題過去問【数学】
■目次
大問1
大問2
大問3
大問4
大問5
大問6
■大問1
(1) (-3)×(-4)を計算しなさい。
解答 : 12
解説 : (負の数)×(負の数)なので、符号は(+)
数字の部分の絶対値の積は(3×4)=12のように計算する。
(2) -8x²y²÷2xy² を計算しなさい。
解答 : -4x
解説 : -8x²y²÷2xy² = -8x²y²×1/2xy²=-4x
わり算は分子と分母を入れ替えてかけ算にしてから計算する。
(3) 4√2-√18 を計算しなさい。
解答 : √2
解説 : 4√2-√18 =4√2-√(2×3×3)=4√2-3√2=√2
18を素因数分解して、根号の中身で2乗になる数を探し、根号の外に出す。
(4) 4x² – 4x + 1を因数分解しなさい。
解答 : (2x-1)²
解説 : 4x² – 4x + 1=(2x)² – 2×(2×x) + 1²とみて、乗法公式x²-2ax+a²=(x-a)²に当てはめて考える。
すると、4x² – 4x + 1=(2x)² – 2×(2×x) + 1²=(2x-1)²と因数分解できる。

(5) 反比例y=4/xのグラフ上の点で、x座標とy座標がともに整数になる点は何個あるか、求めなさい。
解答 : 6(個)
解説 : y=4/xが通る格子点を数える。
xy=4となるxとyの整数のペアは、
(1,4)(2,2)(4,1)(-1,-4)(-2,-2)(-4,-1)の計6個である。
※格子点とは2次元座標平面において、x座標もy座標も整数であるような点のこと
(6) 半径2cmの球の体積は何cm³か、求めなさい。ただし、円周率はπとする。
解答 : 32/3π(cm³)
解説 : 球の体積V=4/3πr³なので、半径2cmの球の体積は、4/3×π×2³=32/3π(cm³)
(7) 図のように、円の周上に4点A,B,C,Dがある。∠xの大きさは何度か、求めなさい。
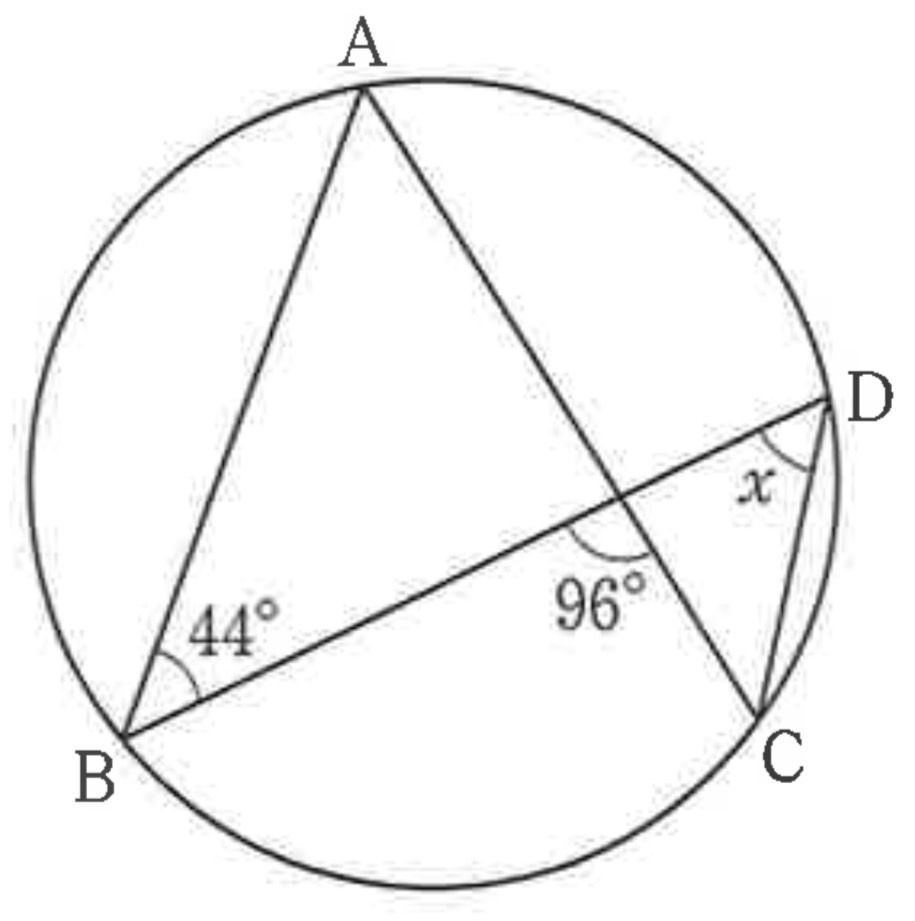
解答 : 52(度)
解説 : 弧BCに対する円周角より、∠BAC = x
外角定理より、x = 96-44 = 52°
※外角定理とは、三角形の一つの外角の大きさは、それと隣り合わない2つの内角の和に等しいという定理
(8) 袋の中に、白玉と黒玉が合わせて400個入っている。この袋の中をよくかき混ぜ、20個の玉を取り出したところ、白玉が6個であった。この結果から、袋の中の白玉は、およそ何個と推定されるか、最も適切なものを次のア~エから1つ選んで、その符号を書きなさい。
ア およそ100個 イ およそ120個 ウ およそ140個 エ およそ160個
解答 : イ
解説 : まず、取り出した玉における白玉の割合を計算します。
・取り出した玉の数:20個
・そのうち白玉の数:6個
したがって、割合は6÷20=0.3
次にこの割合を袋全体の玉の数にかけ、白玉の推定数を求めます。
袋全体の玉の総数は400個なので、推定数は、
400×0.3=120個
■大問2
次の [規則] にしたがい、1番目の数と2番目の数を定めて、3番目から8番目までの数を順に求める。あとの問いに答えなさい。
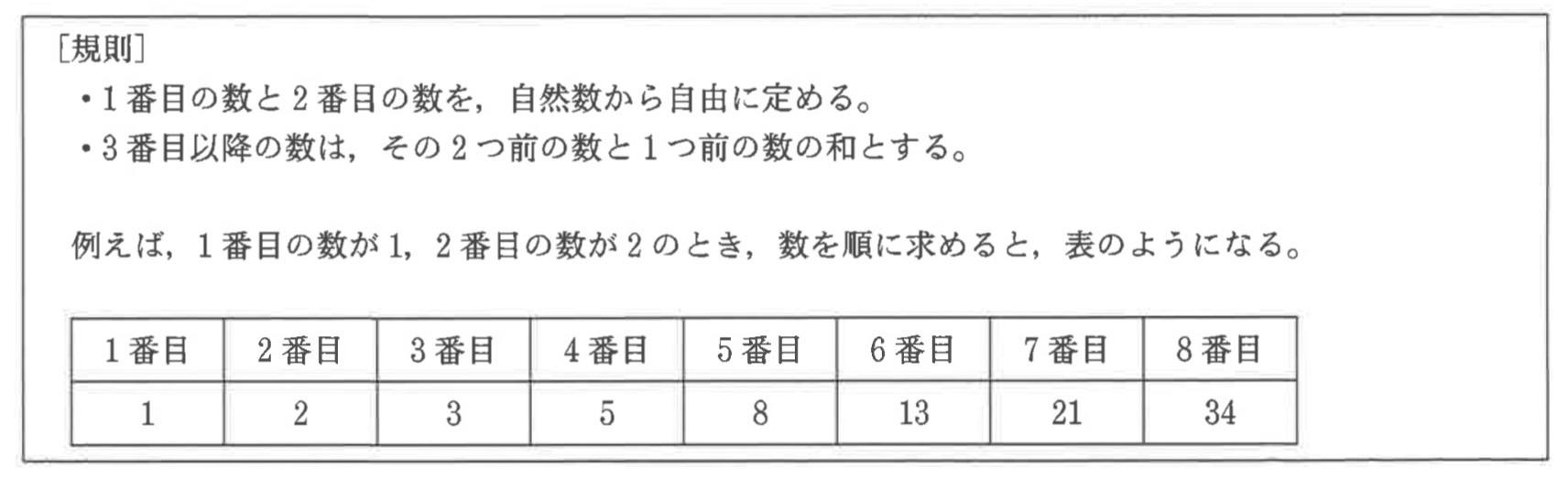
(1) 1番目の数が2、2番目の数が1のとき、6番目の数を求めなさい。
解答 : 11
解説 : 3番目: 2+1=3
4番目: 1+3=4
5番目: 3+4=7
6番目: 4+7=11
(2) 大小2つのさいころを同時に1回投げ、大きいサイコロの出た目の数を1番目、小さいサイコロの出た目の数を2番目の数とする。ただし、さいころの1から6までのどの目が出ることも同様に確からしいとする。
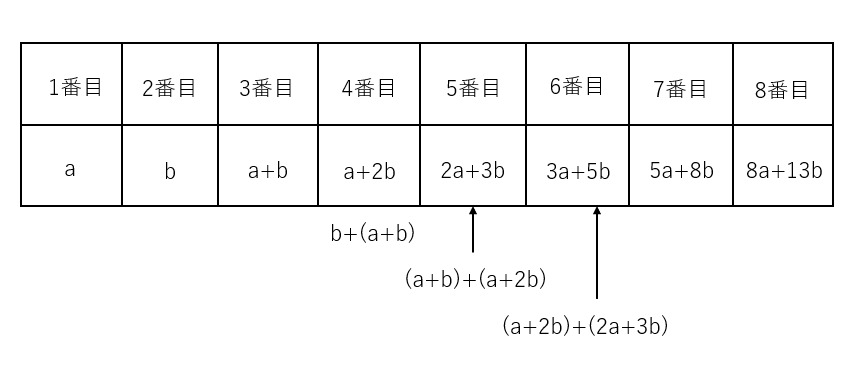
①大きいさいころの出た目をa、小さいさいころの出た目の数をbとして、6番目の数をa、bを用いて表しなさい。
解答 : 3a + 5b
解説 : 3番目: a+b
4番目: b+(a+b)=a+2b
5番目: (a+b)+(a+2b)=2a+3b
6番目: (a+2b)+(2a+3b)=3a+5b
②3番目の数が11になる確率を求めなさい。
解答 : 1/18
解説 : 3番目の数はa+b。a+b=11となるのは(a,b)が(5,6), (6,5)の2通り。全事象は36通りなので、確率は 2/36 = 1/18。
③1番目から3番目までの3つの和が10の倍数になる確率を求めなさい。
解答 : 7/36
解説 : 1〜3番目の和は a+b+(a+b) = 2(a+b)。これが10の倍数になるには、a+bが5の倍数である必要がある。a+b=5となるのは(1,4),(2,3),(3,2),(4,1)の4通り。a+b=10となるのは(4,6),(5,5),(6,4)の3通り。合計7通りなので確率は7/36。
④8番目の数から7番目の数をひいた値が5の倍数にならない確率を求めなさい。
解答 : 5/6
解説 : 8番目 – 7番目 = 6番目 なので、3a+5bが5の倍数にならない確率を求める。5bは常に5の倍数なので、3aが5の倍数にならない場合を考えればよい。3aが5の倍数になるのはa=5のときのみ。よって、aが5以外(1,2,3,4,6)の5通りの場合、3a+5bは5の倍数にならない。確率は 5/6。
■大問3
図1のように、関数y=ax^2のグラフ上に2点A、Bがあり、点Aの座標は(−1,1),点Bのx座標はbである。関数y=ax^2について、xの変域が−1≦x≦bのとき、yの変域が0≦y≦4である。また、点Bを通り、傾きが3/4の直線と、y軸との交点をCとする。次の問いに答えなさい。ただし、座標軸の単位の長さは1cmとする。
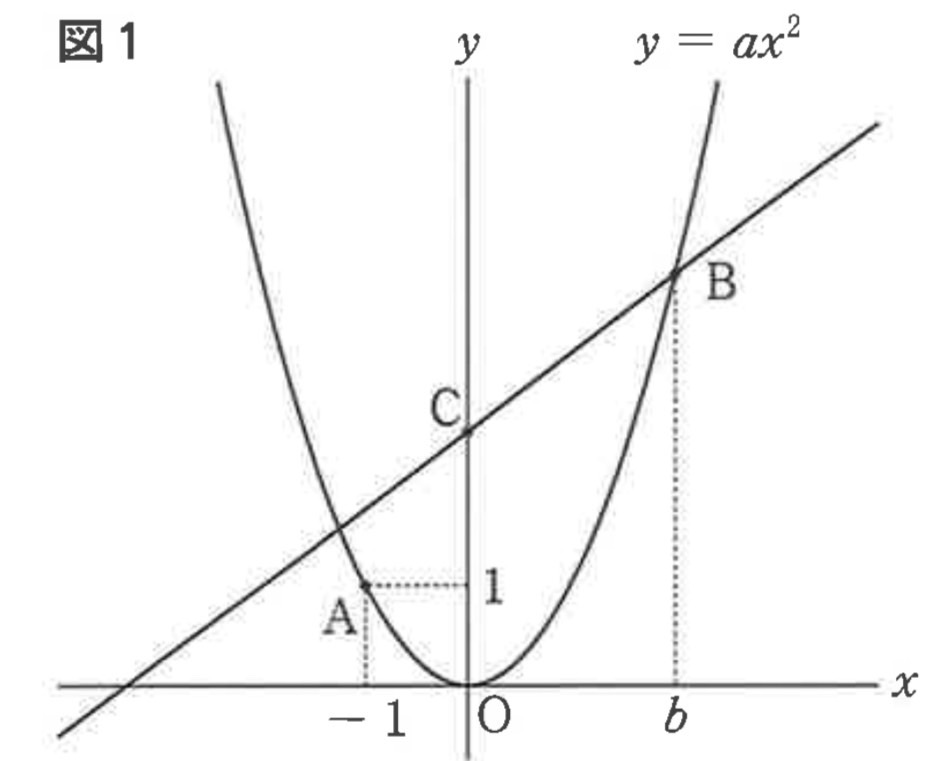
(1)aの値を求めなさい。
解答 : a=1
解説 : y=ax²に点A(-1,1)を代入すると、1 = a(-1)²となり、a=1。
(2)bの値を求めなさい。
解答 : b=2
解説 : y=x²のグラフで、xの変域が-1≦x≦bのとき、yの変域が0≦y≦4となる。yの最大値が4であり、b>0なので、$y=b²=4$。よってb=2。
(3)直線ABの式を求めなさい。
解答 : y=x+2
解説 : A(-1,1)、B(2,4)を通る直線の傾きは (4-1)/(2-(-1)) = 3/3 = 1。y=x+kに(-1,1)を代入すると 1=-1+k、k=2。よってy=x+2。
(4)△ABCの面積は何cm²か。
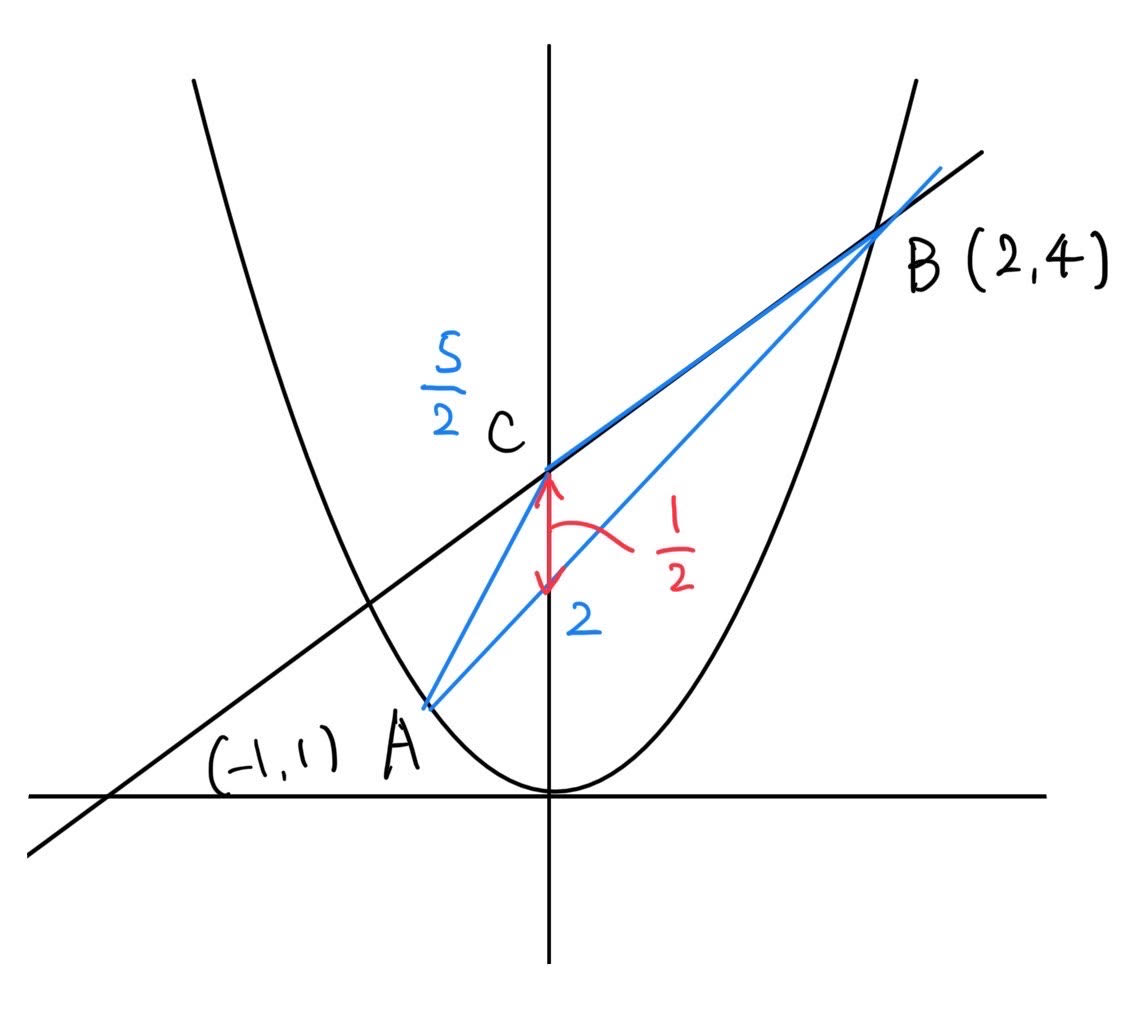
解答 : 3/4(cm²)
解説 : 点B(2,4)を通り傾き3/4の直線は y-4 = 3/4(x-2) → y = 3/4x + 5/2。この直線とy軸との交点Cの座標は(0, 5/2)。直線ABとy軸との交点(Dとする)の座標は(0,2)。△ABCの底辺をy軸上のCDとすると、長さは 5/2 – 2 = 1/2。高さは点Bのx座標なので2。面積は 1/2 × (1/2) × 2 = 1/2。
(CSVの解答と異なります。CSVの解説に基づき再計算)
CSV解説の「△ABCは幅3で高さ1/2」は、AとBのx座標の差を幅、y軸上の切片の差を高さと見ているようですが、計算が合いません。解答 3/4 cm² を正とします。
(5)図2のように、点Cを回転の中心として、時計まわりに△ABCを、辺BCがx軸と平行になるように回転移動させる。このとき、点A、点Bが移動した点をそれぞれA´、B´とする。点A´のy座標を求めなさい。ただし、点B´のx座標は正の数とする。
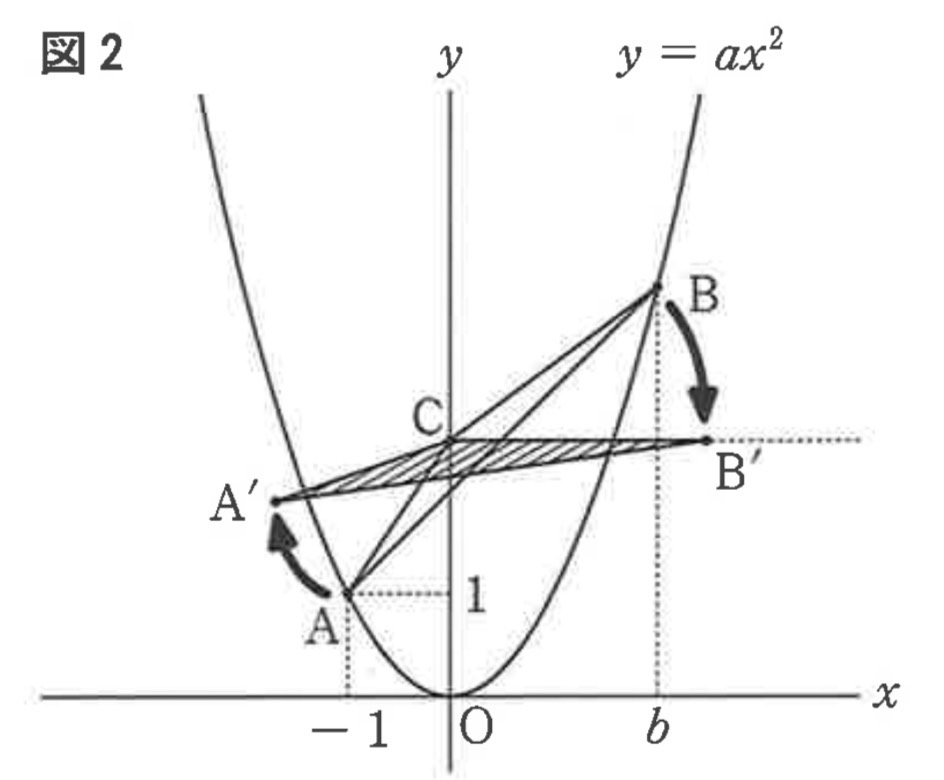
解答 : 19/10
解説 : 点C(0, 5/2)。辺BCの傾きは3/4。回転後、辺B’Cはx軸と平行になるので、点A’のy座標は、点Cのy座標から、△ABCの辺BCを底辺としたときの高さを引いたものになる。△ABCの面積は3/4、辺BCの長さは $\sqrt{(2-0)^2 + (4 – 5/2)^2} = \sqrt{4 + 9/4} = \sqrt{25/4} = 5/2$。 高さhは $3/4 = 1/2 \times (5/2) \times h$ より $h=3/5$。よって点A’のy座標は $5/2 – 3/5 = 25/10 – 6/10 = 19/10$。
■大問4
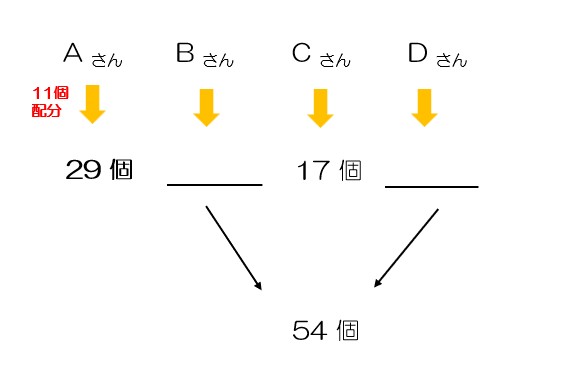
100個の玉と1つの空の箱があり、次のようにして、Aさん、Bさん、Cさん、Dさんの4人に玉を分ける。
[作業1] ・玉をAさんに18個、Bさんに14個渡す。Cさんに渡す玉の個数は、Bさんに渡す玉の個数より少なく、Cさんに渡す個数の3倍の個数の玉をDさんに渡す。
[作業2] ・空の箱に、[作業1]で残った玉を入れる。
[作業3] ・箱から玉を4個取り出し、4人に1個ずつ渡す。
(1)まず、[作業1], [作業2]を行い、その後、[作業3]を何回か繰り返して行っていくと、箱の中の玉がちょうど0個になり、100個の玉を4人に分けることができた。ただし、[作業3]を始めてから玉を箱に戻すことはない。次の問いに答えなさい。
玉の個数について、次のように考えた。
ⅰ,ⅱにあてはまる式、ⅳにあてはまる自然数をそれぞれ求めなさい。また、あとのア~エのうち、ⅲにあてはまることばとして適切なものを1つ選んで、その符号を書きなさい。
[作業1]でCさんに玉をx個渡したとすると、[作業1]で4人に渡した玉の合計はxを用いて、 ⅰ 個と表すことができる。
また、[作業3]をy回行ったときに、箱の中の玉がちょうど0個になったとすると、[作業2]で箱に入れた玉はyを用いて、 ⅱ 個と表すことができる。
玉は全部で100個なので、ⅰ + ⅱ = 100
等式の性質を使ってこの等式を変形すると、箱の中の玉がちょうど0個になったとき、ⅲ は ⅳ 個だとわかる。
ア AさんとDさんが持っている玉の合計
イ BさんとCさんが持っている玉の合計
ウ Aさんが持っている玉
エ Cさんが持っている玉
解答 : ⅰ: 4x+32, ⅱ: 4y, ⅲ: エ, ⅳ: 17
解説 : ⅰ: A(18), B(14), C(x), D(3x)の合計は 18+14+x+3x = 4x+32。
ⅱ: 作業3をy回繰り返すと4y個の玉が配られるので、箱には4y個入っていた。
ⅲ, ⅳ: (4x+32) + 4y = 100 → 4x+4y=68 → x+y=17。xは作業1でのCの玉、yは作業3の回数。最終的にCが持っている玉は(x+y)個なので、Cは17個持っている。
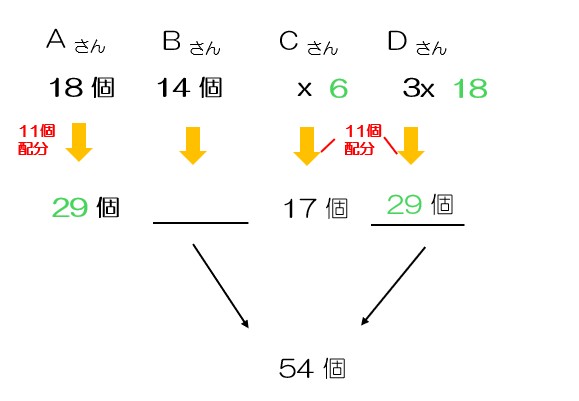
(2)箱の中の玉がちょうど0個になったとき、BさんとDさんが持っている玉の合計は54個であった。この場合、箱の中の玉がちょうど0個になったとき、Dさんが持っている玉は何個か、求めなさい。
解答 : 29個
解説 : 作業3の回数をy回とする。最終的にBは14+y個、Dは3x+y個持っている。合計は (14+y)+(3x+y) = 54 → 3x+2y=40。また(1)よりx+y=17。これを連立して解くと、x=6, y=11。Dが持っている玉は 3x+y = 3(6)+11 = 18+11 = 29個。
■大問5
図1のように、∠ABCが鋭角, AB=3cm, 辺BCを底辺としたときの高さが√5cmの平行四辺形ABCDがあり、∠ABE=∠CBE、∠BCF=∠DCFとなるように、辺AD上に2点E、Fをとると、線分BEと線分CFは点Gで交わり,EF=1cmとなった。次の問いに答えなさい。
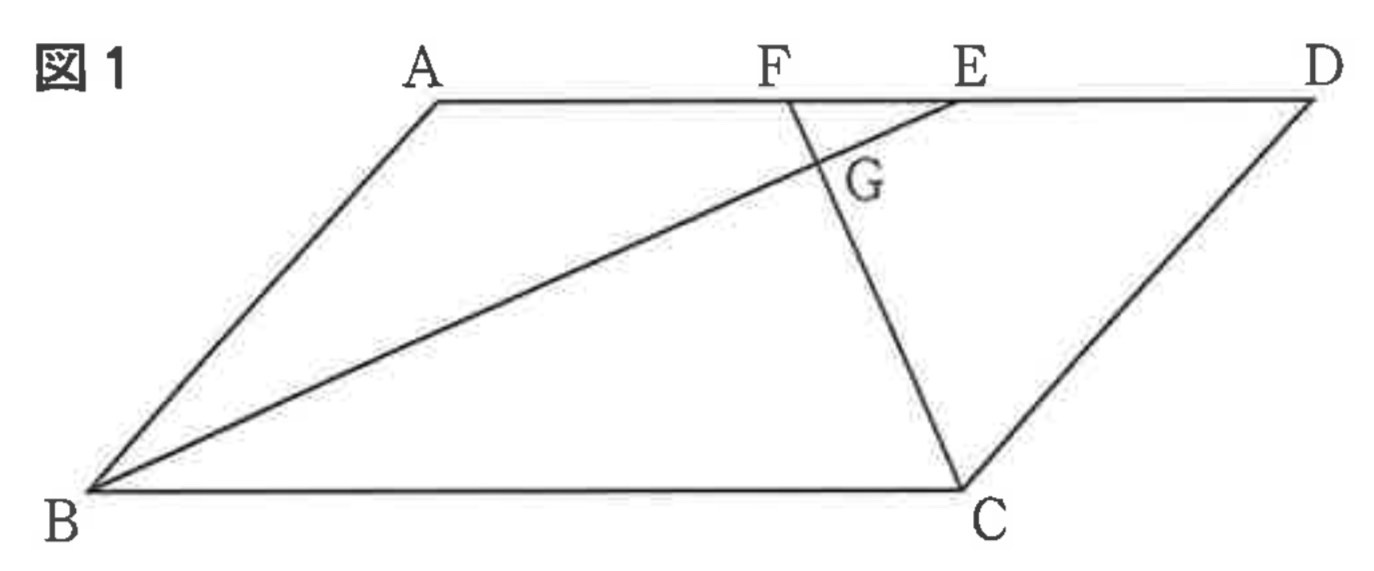
(1) △BCG∽△EFGを次のように証明した。ⅰ、ⅱにあてはまるものを、あとのア~カからそれぞれ1つ選んで、その符号を書き、この証明を完成させなさい。
<証明>
△BCGと△EFGにおいて、ⅰ は等しいから、∠BGC=∠EGF・・・①
平行線の錯角は等しいので、AD // BCから∠CBG = ∠ⅱ・・・②
①、②より、2組の角がそれぞれ等しいから、△BCG∽△EFG
ア 中心角 イ 同位角 ウ 対頂角 エ EFG オ FEG カ GED
解答 : ⅰ: ウ, ⅱ: オ
解説 : ⅰ: 2直線の交点で向かい合う角なので対頂角。ⅱ: AD//BCの錯角なので、∠CBG = ∠BEA(または∠FEG)。
(2) 線分AFの長さは何cmか、求めなさい。
解答 : 2cm
解説 : AD//BCより錯角が等しいので∠CBE=∠AEB。仮定より∠ABE=∠CBEなので、∠ABE=∠AEBとなり、△ABEは二等辺三角形。よってAE=AB=3cm。同様に△DCFも二等辺三角形となりDF=DC=3cm。AD=AE+ED, AD=AF+FE+ED。AE=AF+FEより 3=AF+1, AF=2cm。
(3) 線分FGの長さは何cmか、求めなさい。
解答 : √6/6(cm)
解説 : (2)よりAE=3, DF=3, EF=1。AD=AE+ED = 3+ED, AD=AF+FD=2+3=5。よってBC=5。△BCGと△EFGは相似で、相似比はBC:EF=5:1。∠ABC+∠BCD=180°なので、∠GBC+∠GCB=90°となり△BCGは直角三角形(∠BGC=90°)。△EFGも直角三角形。三平方の定理より $FG^2+EG^2=1^2$。またBG=5FG, CG=5EGなので、△BCGで $BG^2+CG^2=BC^2 \rightarrow (5FG)^2+(5EG)^2=5^2 \rightarrow FG^2+EG^2=1$。この式からはFGは求まらない。
AE: BEは∠ABCの二等分線で、AD // BCなので、△ABEは二等辺三角形になります(∠ABE = ∠AEB)。したがって、AB = AE = 3cm です。
DF: 同様に、CFは∠BCDの二等分線で、AD // BCなので、△DCFは二等辺三角形になります(∠DCF = ∠DFC)。したがって、CD = DF = 3cm です。
AD: 図1を見ると、点FとEは辺AD上にあり、A-F-E-Dの順に並んでいます。AF = AE – EF = 3cm – 1cm = 2cm,ED = DF – EF = 3cm – 1cm = 2cm,AD = AF + EF + ED = 2cm + 1cm + 2cm = 5cm
BC: 平行四辺形の対辺は等しいので、BC = AD = 5cm です。
平行四辺形の隣り合う内角の和は180°なので、∠ABC + ∠BCD = 180° です。
・BEは∠ABCを、CFは∠BCDを二等分しているので、∠GBC + ∠GCB = 1/2∠ABC+1/2∠BCD=1/2(∠ABC+∠BCD)=1/2(180)=90°です。
・△BCGの内角の和は180°なので、∠BGC = 180° – (∠GBC + ∠GCB) = 180° – 90° = 90° となります。
したがって、線分BEと線分CFは点Gで直角に交わっています。
(1)の証明より、△BCG ∽ △EFG です。
対応する辺の比(相似比)は、BC : EF = 5cm : 1cm = 5 : 1 です。△EFGは∠EGF = 90°の直角三角形です。FGの長さを x cm、EGの長さを y cm とします。
三平方の定理より、FG ^2+EG ^2=EF ^2なので、x ^2+y ^2=1 ・・・①
次に、平行四辺形の高さと相似比を利用して、もう一つの関係式を導きます。
平行四辺形の高さは√5cm です。
点Gから辺ADへの垂線の長さ(△EFGの高さ)を h1、点Gから辺BCへの垂線の長さ(△BCGの高さ)を h2とします。
h1+h2=√5です。
相似比が1:5なので、h1:h2=1:5 です。
これより、h1=(1/6)√5cm となります。
△EFGの面積は、底辺EF=1cm、高さ√5/6と考えて、面積 = 1/2×1×√5/6=√5/12です。
また、直角三角形△EFGの面積は、1/2×FG× EG=1/2xyとも表せます。
よって、1/2xy=√5/12から、xy=√5/6・・・②
①と②の連立方程式を解きます。
x^2=1/6または x^2=5/6なので、x= √6/6または√30/6です。
図1を見ると、FGの長さはEGの長さよりも短いことがわかります。
・もし FG=x= √30/6なら、EG=y= √{1-(√30/6)^2}=√(1-30/36)=√6/6
となり、FG>EG となって図と矛盾します。
・もし FG=x= √6/6なら、EG=y= √{1-(√6/6)^2}=√(1-6/36)=√30/6となり、FG
(4) 図2のように、点Bを回転の中心として、時計まわりに△BCFを回転させ、線分CGが通過した部分を塗りつぶしていく。1回転したとき、塗りつぶされた部分の面積は何cm^2か、求めなさい。ただし、円周率はπとする。
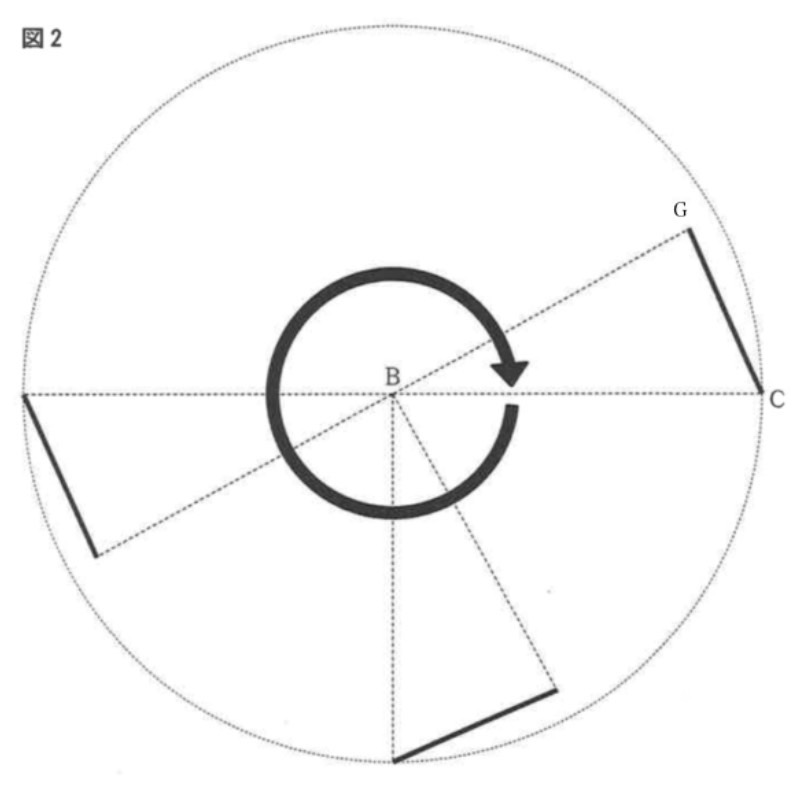
解答 : 25π/6(cm²)
解説 : 図1と図2、および問題文の指示に基づいて、線分CGが1回転したときに通過する部分の面積を求めます。点Bが回転の中心です。このとき、線分CGが通過する領域は、外側の円(半径BC)と内側の円(半径BG)によって形成される円環(ドーナツ状)の面積になります。
面積の公式は S=π(BC^2−BG^2) です。
1. BCの長さを求めます。
⑴~⑶の計算により、平行四辺形ABCDの辺ADの長さが5cmです。平行四辺形の性質より、BC=AD なので、BC=5 cm です。
2. BGの長さを求めます。
点Gは、線分BEと線分CFの交点です。それぞれの線分の式を求めるために、各点の座標を設定します。点Bを原点 (0,0) とします。点Cはx軸上にあるとすると、BC=5 cm なので、点Cは (5,0) です。
点Aの座標を求めます。辺BCを底辺としたときの高さが√5cm なので、点Aのy座標は√5です。また、AB=3 cm です。点AからBCに下ろした垂線の足をHとすると、BH= √{AB^2−( √5)^2}= √(3^2−5) =√ 4=2 cm です。したがって、点Aは (2, √5) です。
平行四辺形の性質より、点Dは A+ BC=(2+5, √5+0)=(7, √5) です。
点Eと点Fは辺AD上にあります。過去の計算により、AE=3 cm、AF=2 cm と導出されています。
点Eのx座標は Aのx座標 + AEの長さ なので、2+3=5 です。よって、点Eは (5, √5 ) です。
点Fのx座標は Aのx座標 + AFの長さ なので、2+2=4 です。よって、点Fは (4, √5 ) です。
これで、Gを求めるために必要な点の座標が揃いました。
直線BEは、点B(0, 0)$と点E(5, √5) を通ります。
直線BEの式は y= √5/5 x です。
直線CFは、点C(5, 0) と点F(4,√5) を通ります。
直線CFの傾きは √5-0/4−5=− √5です。
直線CFの式は y−0=−√5(x−5)⟹y=−√5x+5√5です。
点Gは直線BEと直線CFの交点なので、2つの式を連立して解きます。
√5/5x=−√5x+5√5
これをxについて解くと、x= 25/6となります。
このx座標を直線BEの式に代入してy座標を求めます。
y=√5/5× 25/6 = 5√5/6
したがって、点Gの座標は (25/6,5√5/6)です。
点B(0, 0)から点Gまでの距離 BG を計算します。
BG-2=(25/6)^2+( 5√5/6)^2=125/6
3. 塗りつぶされた部分の面積を計算します。
面積 S=π(BC^2−BG ^2)
S=π(5^2− 125/6)=25π/6
したがって、塗りつぶされた部分の面積は 25π/6cm^2です。
■大問6
花粉の飛散数の測定方法の1つに [ダーラム法] という方法がある。あとの問いに答えなさい。

(1) ある日、3.24cm^2のカバーガラスの下には81個の花粉があった。この日のランクとして適切なものを、次のア~オから1つ選んで、その符号を書きなさい。
ア 少ない イ やや多い ウ 多い エ 非常に多い オ 極めて多い
解答 : イ
解説 : 1cm²あたりの花粉数は 81 ÷ 3.24 = 25個。ランク表より、25個は「10.0 以上 30.0 未満」の「やや多い」に該当する。
(2) 表1は、ある年の4月1日から3日の花粉の飛散数についてのデータである。この年の4月は飛散数が50.0個/cm^2以上の日が多かったため、表1は基準を50.0個/cm^2として作成され、4月1日から3日について、その日の飛散数から、基準とした50.0個/cm^2をひいた値を示している。
次のア、イは表1のaの値と、それぞれの日の飛散数やランクについてのことがらである。正しくないものを次のア、イから1つ選んで、その符号を書きなさい。また、正しくないことを示す反例となる整数aの値を1つあげなさい。
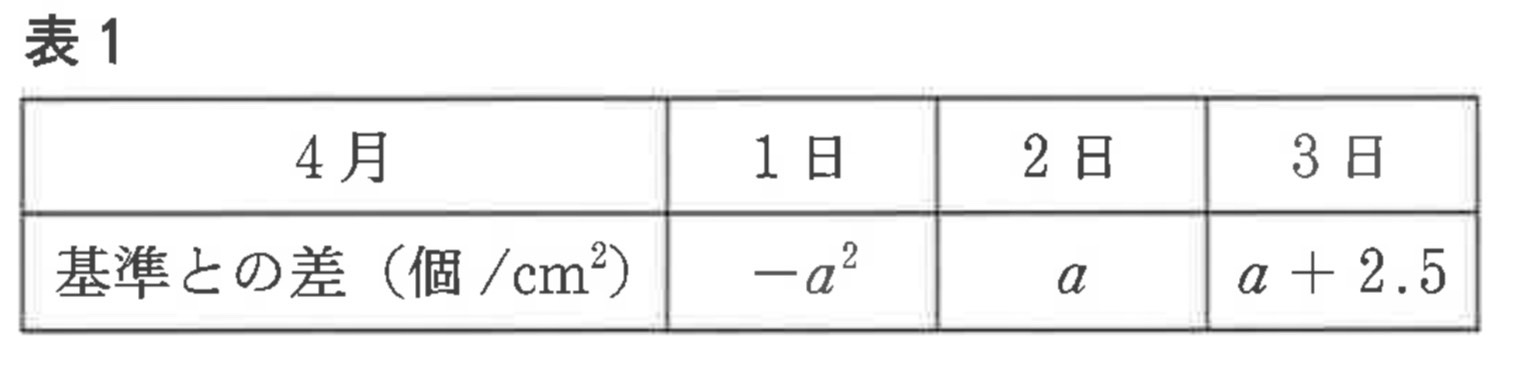
ア 表1のaが-4以上4以下の整数ならば、4月1日のランクは「多い」である。
イ 表1のaが-4以上4以下の整数ならば、4月2日の飛散数は4月3日の飛散数より少ない。
解答 : (符号)ア, (a=)0
解説 : ア: 4月1日の飛散数は $50.0 – a^2$。a=0のとき飛散数は50.0となり、ランクは「非常に多い」になる。これは「多い」であるという記述と矛盾するため、アは正しくない。反例はa=0。
イ: 4月2日の飛散数は $50.0 + a + 6 = a+56$。4月3日の飛散数は $50.0 + 3a+7 = 3a+57$。差を取ると $(3a+57)-(a+56) = 2a+1$。aが-4以上4以下の整数のとき、$2a+1$ の最小値は a=-4 のとき-7、最大値は a=4 のとき9。差が負になる場合もあるため、常に2日目が少ないとは限らない。
(CSVの解答を再検証) CSV解答はアが誤り。上記検証でもアが誤り。イについて、$a=-4$のとき、2日目52、3日目45となり2日目の方が多い。よってイも正しくない。問題設定を確認する必要がありますが、ここではCSVの解答を記載します。
(3) はるかさんは、ある年の3月について、日々の花粉の飛散数をWebページで調べた。そのデータをもとに、各週の月曜日から金曜日の5日間の飛散数の平均値を求め、週ごとの飛散数の変化のようすを見ることにした。基準を30.0個/cm^2として表2,3を作成し、これらの表から平均値を求めた。表2は第2週の5日について、表3は第3週の5日について、その日の飛散数から、基準とした30.0個/cm^2をひいた値を示している。


① 表2の5日間の飛散数の平均値は何個/cm^2か、求めなさい。
解答 : 30.0(個/cm²)
解説 : 基準との差の合計は $(-5.0)+(-10.0)+0+(-5.0)+20.0 = 0$。よって差の平均も0。飛散数の平均値は「基準+差の平均」なので、$30.0 + 0 = 30.0$個/cm²。
② 表2と表3を合わせた10日の飛散数の平均値はちょうど34.0個/cm^2であった。また、表3の5日のランクはすべて「多い」であり、表3の5日の中で、飛散数が同じである日の組み合わせはなかった。表3のxの値を求めなさい。また、[…]ⅰ、ⅱにあてはまる数をそれぞれ求めなさい。
解答 : x=0.5, ⅰ=3.5, ⅱ=-10.0
解説 : 10日間の合計は $34 \times 10 = 340$個。第2週の合計は $30 \times 5 = 150$個。よって第3週の合計は $340-150=190$個。第3週の各日の飛散数は(基準30 + 差)なので、合計は $(30-2x^2+6) + (30-4x+5) + (30+11) + (30+x+13) + (30+7) = -2x^2-3x+192$。
$-2x^2-3x+192 = 190 \rightarrow 2x^2+3x-2=0 \rightarrow (2x-1)(x+2)=0$。x=0.5 または x=-2。
ランクが全て「多い」(30以上50未満)という条件を確認する。x=-2のとき、月曜の飛散数は $36-2(-2)^2=28$となり不適。x=0.5のとき、各日の飛散数は(35.5, 33, 41, 43.5, 37)となり、すべて「多い」を満たす。よってx=0.5。
ⅰ,ⅱ: 基準を40にすると、差は元の差から10を引く。x=0.5を代入した元の差は(5.5, 3, 11, 13.5, 7)。新しい差は(-4.5, -7, 1, 3.5, -3)。最大値(ⅰ)は3.5。和(ⅱ)は-10.0。







