令和7年度_学力検査問題過去問【福岡】

■問題PDF　

■目次　

■大問１

⑴　5−2×(−7) を計算しなさい 。

解答 ： 19

解説 ：※かけ算から解いていきます。
5-2×(-7)
=5+14
=19

⑵　3(a+b)−(a−4b) を計算しなさい 。

解答 ： 2a+7b

解説 ：3(a+b)−(a−4b)
=3a+3b-a+4b
=2a+7b

⑶　a=4,b=−5 のとき、9a²b÷(−3a) の値を求めなさい 。

解答 ： -60

解説 ：まず、与えられた式 9a²b÷(−3a) を簡略化します。
[9a²b]/[−3a]
=-3ab・・・①
①にa=4,b=−5 を代入します。
-3×4×-5=-60

⑷　√48-6/√3を計算しなさい 。

解答 ： 2√3

解説 ：6/√3を有利化すると、
6/√3=[6√3]/3=2√3 となります。
√48=√[2×2×2×2×3]=4√3なので
4√3-2√3=2√3

⑸　9a²−25b²を因数分解しなさい 。

解答 ： (3a+5b)(3a-5b)

解説 ：

この式は、平方の差の公式 x²−y²=(x−y)(x+y) を使って因数分解できます。
まず、9a²−25b²を平方の形に変形します。
9a²は (3a)²と表せます。
25b²は (5b)²と表せます。
これらの結果を平方の差の公式に当てはめます。
x を 3a に、y を 5b に置き換えます。
(3a)²−(5b)²=(3a−5b)(3a+5b)

⑹　関数y=2x²について、x の変域が −1≤x≤2 のとき、y の変域を求めなさい 。

解答 ： 0≦y≦8

解説 ：

関数 y=2x²は、原点 (0,0) を頂点とする下に凸の放物線です。x の変域 −1≤x≤2 の中に、頂点の x 座標である x=0 が含まれています。したがって、y の最小値は x=0 のときになります。
x=0 を式に代入すると、y=2×0²=0 となります。
よって、最小値は 0 です。
放物線は頂点から離れるほど y の値が大きくなります。x の変域 −1≤x≤2 の中で、頂点 x=0 から最も遠いのは、絶対値が最も大きい x の値です。
|−1|=1
|2|=2
2 の方が −1よりも大きいため、x=2 のときに y の値が最大になります。
x=2 を式に代入すると、y=2×2²=2×4=8 となります。
よって、最大値は 8 です。
これらのことから、y の変域は最小値0から最大値8までとなり、0≤y≤8 となります。

⑺　関数 y=−3/xのグラフをかきなさい 。

解答 ：

解説 ：

関数 y=−3/xのグラフは、反比例のグラフで、原点を中心に対称な 双曲線になります。x>0 の範囲では第2象限に、x<0 の範囲では第4象限に位置します。x=-3,-1,1,3をy=-3/xの式に代入してそれぞれのyの値を求めます。x=−3 のとき: y=1
x=−1 のとき: y=3
x=1 のとき: y=−3
x=3 のとき: y=−1
これらの点 (−3,1), (−1,3), (1,−3), (3,−1) を座標平面上にプロットし、それぞれ滑らかな曲線で結ぶと、グラフが完成します。

⑻　1から6までの目が出る2つのさいころA、Bを同時に投げる 。さいころAの出る目を十の位の数、さいころBの出る目を一の位の数としてできる2桁の自然数が4の倍数になる確率を求めなさい 。
ただし、さいころはどの目が出ることも同様に確からしいとする。

解答 ： 1/4

解説 ：サイコロAとサイコロBを同時に投げるとき、それぞれのサイコロの目の出方は6通りずつあります。したがって、できる2桁の自然数の総数は、6×6=36 通りです。2桁の自然数が4の倍数になる組み合わせは [12, 16, 24, 32, 36, 44, 52, 56, 64] の9通りです。したがって、求める確率は 9/36=1/4 となります。

⑼　白の碁石だけがたくさん入っている袋がある 。この袋に白の碁石と同じ大きさの黒の碁石を50個入れてよくかき混ぜ、この袋から30個の碁石を無作為に抽出したところ、黒の碁石は6個であった 。この袋に入っている白の碁石の個数は、およそ何個と推定できるか答えなさい 。

解答 ： およそ200個

解説 ：抽出した30個のうち、黒が6個、白が24個でした。この標本における白と黒の比は 24:6 = 4:1 です。袋全体（母集団）の比もこれとほぼ等しいと考えられます。袋全体の黒の碁石は50個なので、白の碁石の数をx個とすると、x : 50 = 4 : 1 という比例式が成り立ちます。これを解くと、x = 50 × 4 = 200 となります。

■大問２

希さんは、K中学校の1年生、2年生、3年生のそれぞれの生徒を対象に、1日あたりの睡眠時間について調査した。 表は、K中学校の各学年のデータをそれぞれ度数分布表に生理したものである。 図は、K中学校の各学年のデータをそれ箱ひげ図に表したものである。

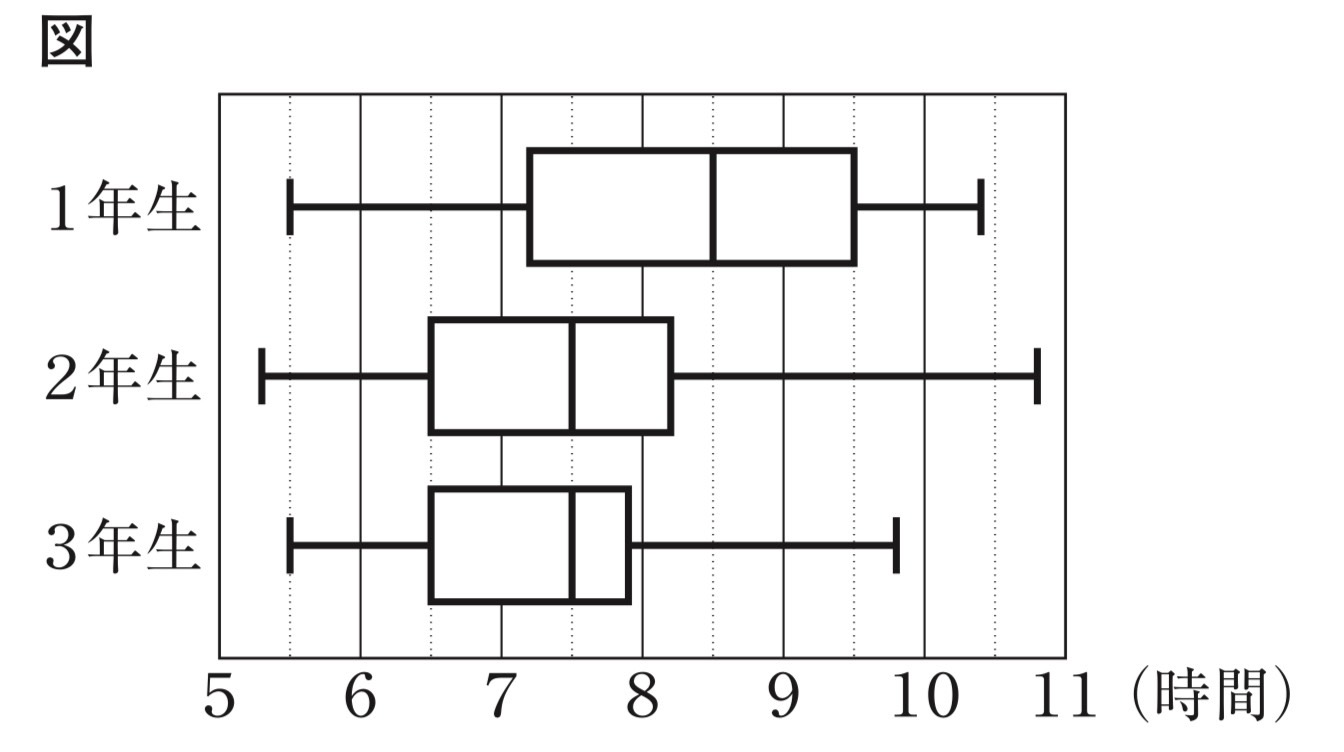
次の⑴～⑶に答えなさい。

⑴表において、各学年のデータの最頻値のうち、データの最頻値が最も大きい学年と、その学年の最頻値を求めなさい 。

解答 ： 学年 1年生　最頻値 8.5時間

解説 ：最頻値とは、最も度数の多い階級の階級値のことです。1年生は「8時間以上9時間未満」（度数23）が最も多く、階級値は(8+9)÷2=8.5時間。2年生と3年生は「7時間以上8時間未満」が最も多く、階級値は7.5時間。これらの最頻値を比較すると、1年生の 8.5時間 が最も大きい値となります。

⑵表や図から読み取れることとして正しいものを、次のア～エからすべて選び、記号で答えなさい 。
ア. K中学校で、睡眠時間が最も短い生徒は、2年生の中にいる 。
イ. 1年生において、睡眠時間が最も長い生徒と最も短い生徒で、5時間以上の差がある 。
ウ. 1年生と2年生において、睡眠時間が9.5時間以上の生徒の人数は、2年生の方が1年生より多い 。
エ. 3年生の生徒の睡眠時間を短い順に並べたとき、21番目の生徒の睡眠時間は、6.5時間である 。

解答 ： ア、エ

解説 ：
ア. 図の箱ひげ図を見ると、2年生のひげの左端（最小値）が、他の学年よりも左にあるため正しいです。
イ. 図を見ると、1年生の範囲はおよそ5.5時間から10.5時間で、差は5時間なので、「5時間以上」とは断定できず誤りです。
ウ. 表から、9.5時間以上の生徒は1年生が19+7=26人、2年生が10+2=12人なので誤りです。
エ. 3年生は83人おり、第1四分位数は小さい方から25%の位置なので、83×0.25=20.75より21番目の生徒です。図の3年生の箱の左端（第1四分位数）は6.5時間なので正しいです。

⑶表をもとに、睡眠時間が7時間未満の生徒の割合が最も大きいのはどの学年であるかを、累積相対度数を用いて説明しなさい 。累積相対度数は四捨入して小数第2位まで求めなさい 。

解答 ：（例）睡眠時間が7時間未満の生徒の割合について、１年生、２年生、３年生のそれぞれの累積相対度数を四捨五入して小数第2位まで求めると、
１年生が、11/79だから0.14
２年生が、19/66だから、0.29
３年生が、27/83だから、0.33
0.33>0.29>0.14なので、睡眠時間が７時間未満の生徒の割合が最も大きいのは、３年生である。

解説 ：睡眠時間が7時間未満の生徒の割合を、各学年で累積相対度数を使って比較します。
考え方①：各学年の累積度数を計算する
睡眠時間が「5時間以上6時間未満」と「6時間以上7時間未満」の階級の度数を合計します。
1年生：3+8=11人
2年生：4+15=19人
3年生：8+19=27人
考え方②：各学年の累積相対度数を計算する
累積度数を、それぞれの学年の合計人数で割って、小数第2位まで四捨五入します。
1年生：11/79 ≒ 0.14
2年生： 19/66 ≒ 0.29
3年生： 27/83 ≒ 0.33
考え方③：比較と結論
この結果から、睡眠時間が7時間未満の生徒の割合が最も大きいのは、3年生であることがわかります。

■大問３

A「2をひく」、B「2倍する」、C「2乗する」、D「はじめの数をひく」という計算方法が かかれた4個の玉A, B, C. Dが袋に入っている。
この袋の中の玉を使って、次の手順によって、計算結果を求める。

手順
① 袋の中から玉を1個ずつ3回続けて取り出し、取り出した順に左から並べる。ただし、取り出した玉は袋にもどさない。
② はじめの数を1つ決める。
③ はじめの数に対して、左の玉にかかれた計算を行う。
④ ③で求めた数に対して、真ん中の玉にかかれた計算を行う。
⑤ ④で求めた数に対して、右の玉にかかれた計算を行う。

図は、例えば、玉がA、B、Cの順に並んだ場合、はじめの数が1のとき、計算結果は 4になることを表している。

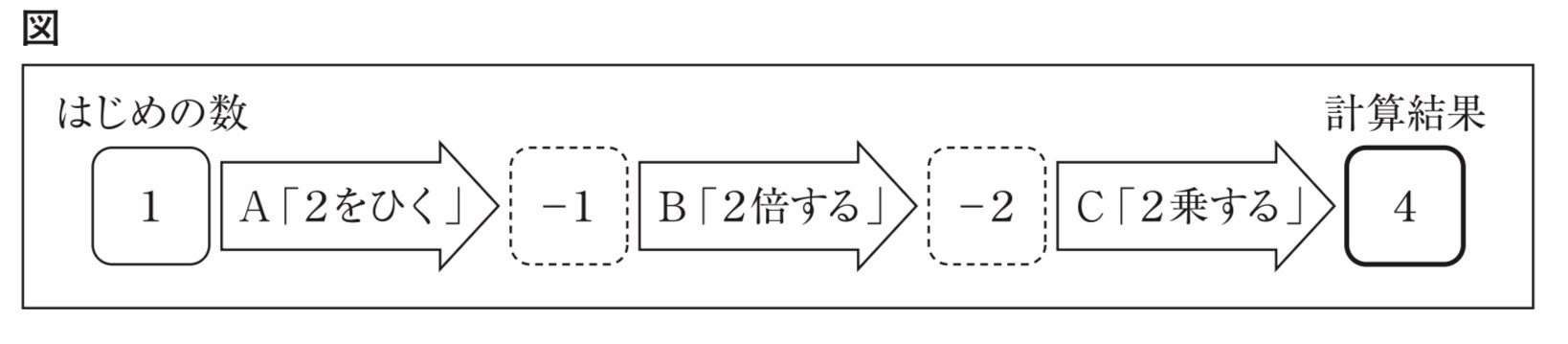
下の会話文は、明さんと光さんが、手順によって、計算結果を求め、はじめの数、玉の 並び方、計算結果の関係について話し合った内容の一部である。

明さん：玉がA、B、Cの順に並んだ場合、はじめの数が5のとき、計算結果は(P) になるよ。
光さん：そうだね。はじめの数は5のままで、玉がB, A, Cの順に並んだ場合、 計算結果は64になるので、はじめの数は変えずに、玉の並び方が変わると、 計算結果は変わりそうだね。
明さん：他にも、玉はB, A, Cの順に並んだままで、はじめの数を3に変えると、 計算結果は16になるよ。このことから、玉の並び方が変わらずに、はじめの数を 変えると、計算結果は変わりそうだね。
光さん：でも、調べてみたら、はじめの数をどんな数に変えても、計算結果が常に同じ数に なる玉の並び方があるかもしれないよ。
明さん：どんな並び方かな。文字式を使って調べてみようよ。

次の⑴～⑷に答えなさい。

⑴手順①において、玉の並び方は全部で何通りあるか求めなさい。

解答 ： 24通り

解説 ：この問題は、4個の玉（A, B, C, D）から3個を選んで順に並べる場合の数を求める、順列の問題です。1番目の玉の選び方は4通り、2番目は3通り、3番目は2通りです。したがって、玉の並び方の総数は、4×3×2=24通りとなります。

⑵(P)にあてはまる数を求めなさい。また、玉がA、B、Dの順に並んだ場合、計算結果が10になるときの、はじめの数を求めなさい。

解答 ： ℗ 36　はじめの数 14

解説 ：
(P)の計算：はじめの数が5で、玉の並びがA, B, Cの順の場合。A(2をひく)：5−2=3 → B(2倍する)：3×2=6 → C(2乗する)：6²=36。よって(P)は36。
はじめの数の計算：玉がA, B, Dの順で結果が10になる場合。はじめの数をxとする。A(2をひく)：x−2 → B(2倍する)：2(x−2)=2x−4 → D(はじめの数をひく)：(2x−4)−x=x−4。これが10になるので、x−4=10 → x=14。

⑶ 明さんと光さんが、下線部について調べた結果、玉の並び方にはいずれもDが ふくまれていることがわかった。その並び方のうち、真ん中の玉がDのときの玉の並び方 と計算結果について、次のようにまとめた。

まとめ
真ん中の玉がDのとき、はじめの数をどんな数に変えても計算結果が常に同じ数 になる玉の並び方と、そのときの計算結果の組み合わせは、次の2通りである。
Ⅰ 玉がア,D,イの順に並んだ場合、計算結果は常に(Q)になる。
Ⅱ 玉がウ,D,エ の順に並んだ場合、計算結果は常に (R)になる。

ア～エにあてはまる記号を、それぞれA、B、Cから選んでかきなさい。 また、(Q), (R) にあてはまる数を求めなさい。

解答 ： ア A　イ B　Ⓠ -4　ウ A　エ C　® 4

解説 ：
[ア, D, イ の並び方（A, D, B）の場合]
A「2をひく」：はじめの数 x から2を引くので、x−2 となります。
D「はじめの数をひく」：1で求めた数 x−2 から、はじめの数 x を引くので、(x−2)−x=−2 となります。ここでxが消えるため、この後の計算結果ははじめの数に関係なく一定になります。
B「2倍する」：2で求めた数 −2 を2倍するので、−2×2=−4 となります。
したがって、玉の並び方がA, D, Bのとき、計算結果は常に-4になります。

[ウ, D, エ の並び方（A, D, C）の場合]
A「2をひく」：はじめの数 x から2を引くので、x−2 となります。
D「はじめの数をひく」：1で求めた数 x−2 から、はじめの数 x を引くので、(x−2)−x=−2 となります。ここでもxが消え、後の計算結果は一定になります。
C「2乗する」：2で求めた数 −2 を2乗するので、(−2)²=4 となります。
したがって、玉の並び方がA, D, Cのとき、計算結果は常に4になります。

(4) 玉がA. C. Bの順に並んだ場合と、玉がB. C. Aの順に並んだ場合について、 はじめの数が同じ数で、それぞれの計算結果が等しくなるときの、はじめの数を全て求めなさい。

解答 ： -5,1

解説 ：[玉がA, C, Bの順の場合]
A「2をひく」: x−2
C「2乗する」: (x−2)²=x²−4x+4
B「2倍する」: 2(x²−4x+4)=2x²−8x+8

[玉がB, C, Aの順の場合]
B「2倍する」: 2x
C「2乗する」: (2x)²=4x²
A「2をひく」: 4x²−2

両方の計算結果を等しいと置きます。
2x²−8x+8=4x²−2
この方程式を解くと
0=4x²−2x²+8x−2−8
0=2x²+8x−10
両辺を2で割ります。
0=x²+4x−5
この2次方程式を因数分解します。
(x+5)(x−1)=0
したがって、解は x=−5 と x=1 です。

■大問４

A駅、B駅、C駅がこの順に一直線の線路上にあり、A駅からB駅までは4800m. A駅から C駅までは7200m離れている。電車Pは、午前8時にA駅を出発し、B駅に向かって 一定の速さで12分間進み、B駅に到着した。B駅で3分間停車した後、B駅からC駅まで 分速480mで進み、午前8時20分にC駅に到着した。
図は、午前8時からx分後に電車PがA駅からym離れているとするとき、午前8時から 午前8時20分までのxとyの関係をグラフに表したものである。

次の(1)~(4)に答えなさい。

(1) 電車PがA駅から3000m離れているのは、電車PがA駅を出発してから何分何秒後か求めなさい。

解答 ： 7分30秒後

解説 ：グラフから、電車PはA駅からB駅まで12分で4800m進んでいるので、速さは 4800m ÷ 12分 = 400m/分です。3000m進むのにかかる時間は、3000m ÷ 400m/分 = 7.5分。0.5分は30秒なので、7分30秒後となります。

(2) 次のア~エの表のうち、電車Pの午前8時16分から午前8時18分までのxとyの関係を正しく表したものが1つある。それを選び、記号をかきなさい

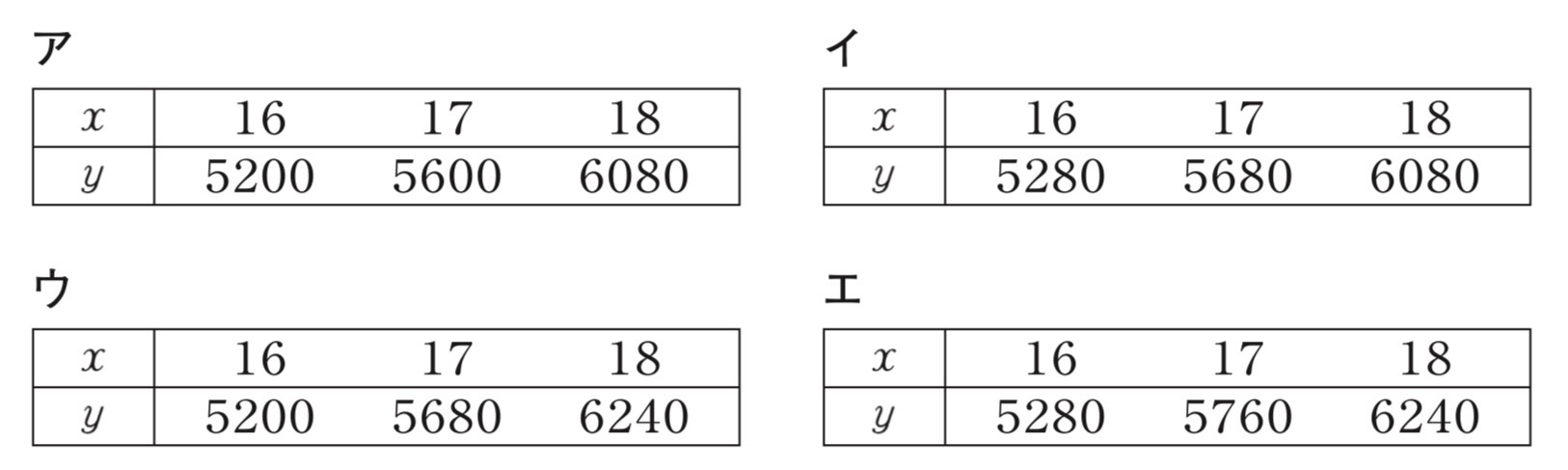
解答 ： エ

解説 ：B駅からC駅までの速さは問題文より分速480mです。B駅はA駅から4800m地点にあります。各時刻のA駅からの距離を計算します。x=16分(B駅出発1分後): 4800 + 480×1 = 5280m。x=17分(B駅出発2分後): 4800 + 480×2 = 5760m。x=18分(B駅出発3分後): 4800 + 480×3 = 6240m。この計算結果は、エの内容と一致します。

(3) 電車Qは、午前8時4分にA駅を出発し、A駅からC駅まで一定の速さで進む。 電車Qは、電車PがB駅に到着した後にB駅を通過し、電車Pより早くC駅に到着した。 このときの電車Qの速さについて、次のようにまとめた。

まとめ
電車Qの速さは、分速アmより速く、分速 イmより遅い。 ただし、アは、あてはまる数のうち最も小さい数、イはあてはまる数のうち最も大きい数である。

ア、イにあてはまる数を求めなさい。

解答 ： ア 450 イ 600

解説 ：電車Qは、電車PがB駅に到着した後にB駅を通過したことより、電車PがA駅からB駅までかかる時間は12分なので電車PがB駅に到着したのは、午前8時12分です。
電車QがB駅を通過する時刻は、午前8時12分より後なので、電車Qは午前8時4分に出発しており、B駅までの4800mを進むのにかかる時間は、12−4=8分より長い必要があります。
したがって、電車Qの速さをvとすると、4800/v>8となり、v<600m/分となります。

電車Qは、電車Pより早くC駅に到着したことより、電車PがC駅に到着したのは、午前8時20分なので電車QがC駅に到着する時刻は、午前8時20分より前です。
電車Qは午前8時4分に出発しているので、C駅までの7200mを進むのにかかる時間は、20−4=16分より短い必要があります。
したがって、電車Qの速さをvとすると、7200/v<16となり、v>450m/分となります。

上記の2つの条件から、電車Qの速さvは、450アは、あてはまる数のうち最も小さい数なので、450
イは、あてはまる数のうち最も大きい数なので、600

(4) 電車Rは、午前8時14分にC駅を出発し、A駅に向かって一定の速さで進み、B駅と C駅の間で電車Pとすれちがい、午前8時24分にA駅とB駅の間で、A駅から4000m 離れている地点を通過する。
このとき、電車Rが電車Pとすれちがったのは、午前8時何分何秒か求めなさい。

解答 ： 8:17:36

解説 ：[電車Ｒの速さを求めます。]
電車Rは、午前8時14分にC駅を出発しています。
午前8時24分に、A駅から4000mの地点を通過しこの地点は、C駅から 7200−4000=3200m 離れているので、3200mを進むのにかかった時間は、24−14=10分です。
したがって、電車Rの速さは 3200m÷10分=320m/分 です。
[すれ違う時刻を求めます。]
すれ違うのは、電車PがB駅を出発した午前8時15分以降で、この時刻からt分後にすれ違うとすると
電車Pは、B駅（4800m地点）からC駅に向かって 480×tm 進むと表せます。
電車Rは、午前8時14分に出発しているので、午前8時15分からは (t+1)分進んでいます。C駅（7200m地点）からA駅に向かって 320(t+1)m 進みます。
A駅からの距離が等しくなるので、
4800+480t=7200−320(t+1)
この式を解くと、t=2.6分となります。
2.6分は「2分36秒」なので、すれ違う時刻は午前8時15分にこれを足して、午前8時17分36秒です。

■大問５

円Oの円周上に5点A,B,C,D,Eをとり、五角形ABCDEをつくります 。
図1は五角形ABCDEにおいて、点Bと点Eを結び、BE//CDとなる場合を表しています 。

次の⑴～⑶に答えなさい。

(1) 図2は図1において、五角形ABCDEが正五角形となる場合を表しており、点Aと点Cを結び、線分ACと線分BEの交点をGとしたものである。
このとき、∠AGEの大きさを求めなさい 。

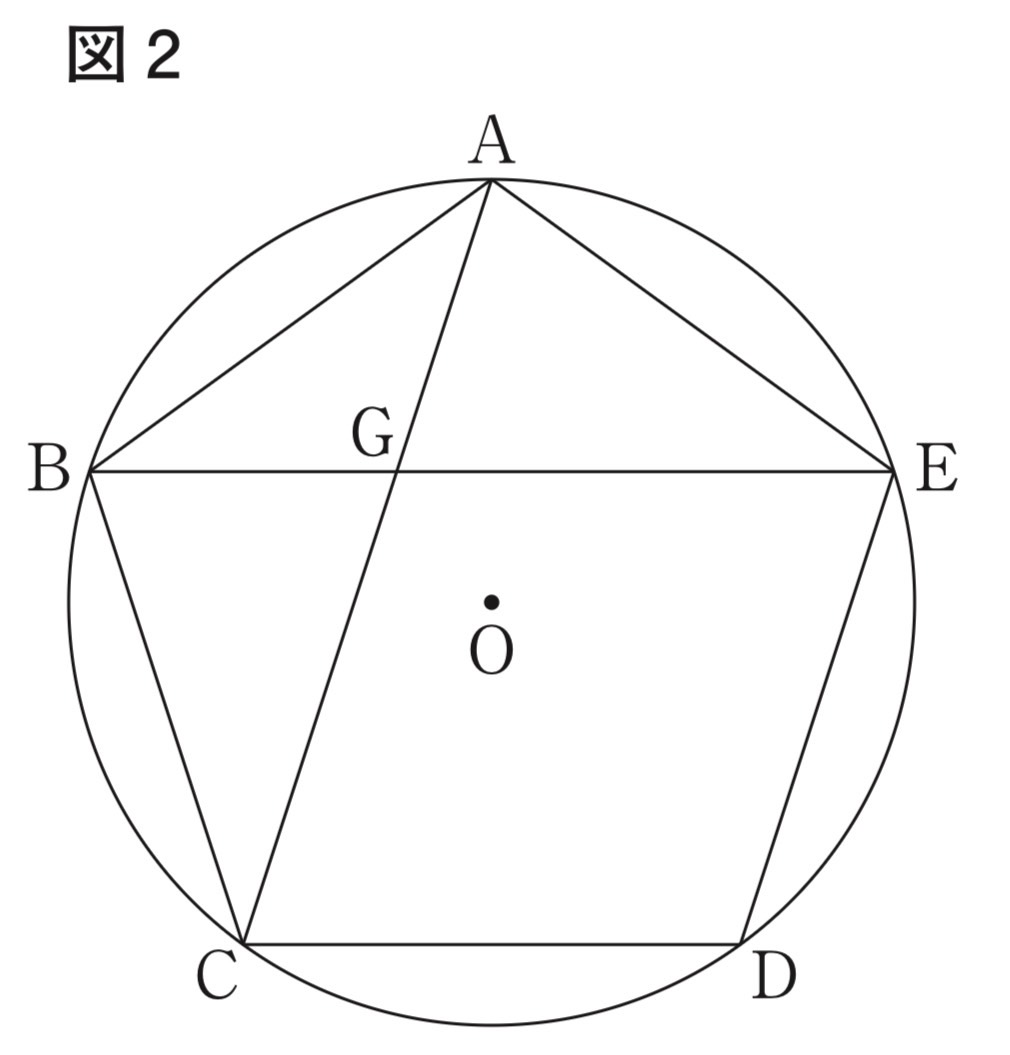
解答 ： 72

解説 ：

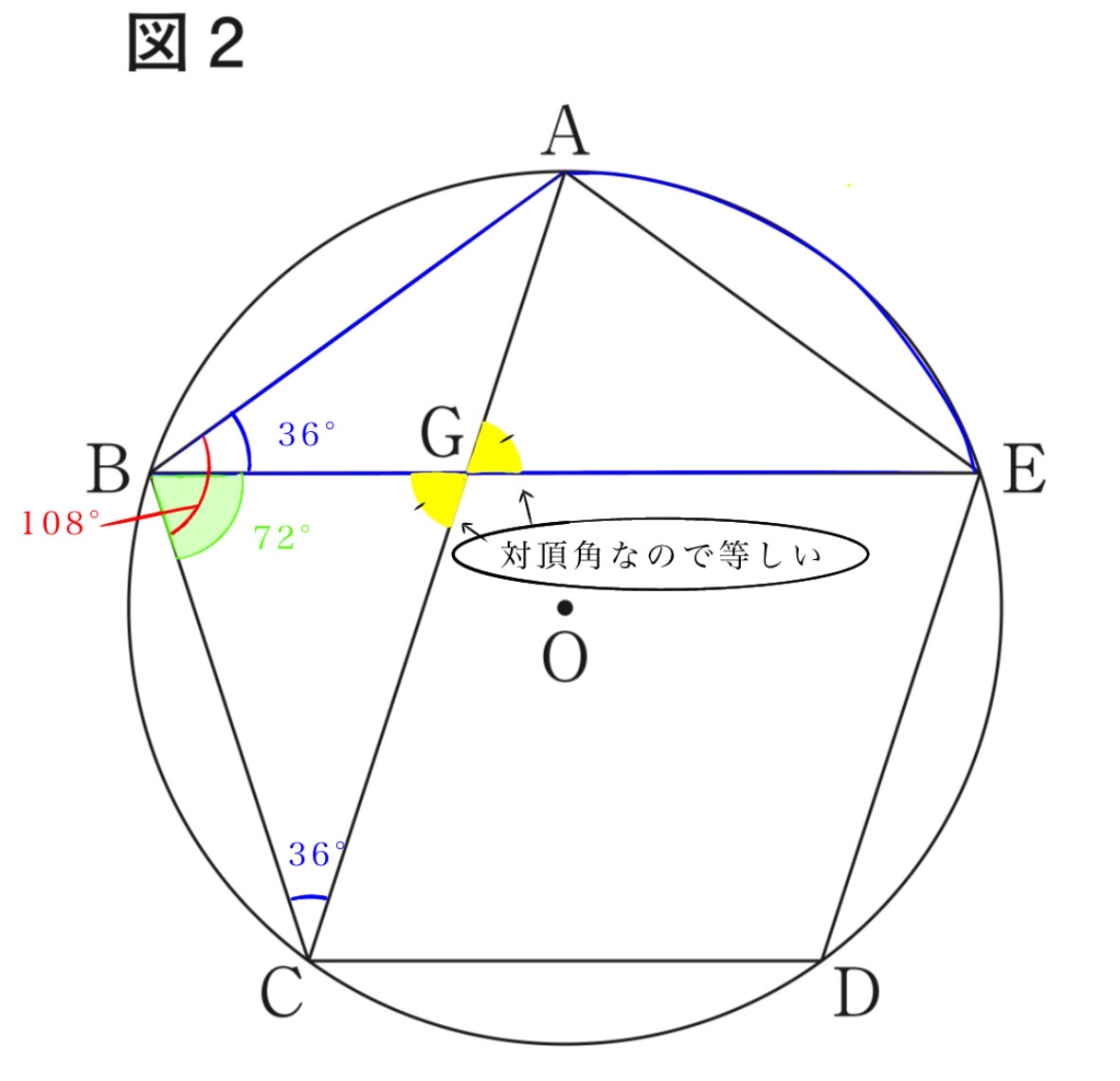
[正五角形の角度を調べる]
正五角形の内角はすべて108°です。
正五角形は円に内接するので、それぞれの頂点の間にある円弧の長さは等しくなります。
したがって、同じ長さの円弧に対する円周角も等しくなります。
弧BCに対する円周角は∠BAC、弧CDに対する円周角は∠CAD…など、すべて等しく、その大きさは 180 ÷5=36°となります。

[△BCGの角度を求める]
求めたい∠AGEの対頂角である∠BGCの大きさを考えます。
△BCGにおいて、∠GBCは内角∠ABCから∠ABEを引いた角度です。
∠ABCは正五角形の内角なので108°です。
∠ABEは、弧AEに対する円周角で、弧ABと弧BCに対する円周角と同じ36°です。
したがって、∠GBC = ∠ABC – ∠ABE = 108 – 36= 72°となります。
もう一つの角、∠GCBは、∠BCAと同じ36°です。
よって、∠BGC = 180 – (72+ 36) = 180-108 = 72°となります。

[∠AGEの大きさを求める]
∠AGEと∠BGCは対頂角なので、その大きさは等しくなります。
∠AGE=∠BGC=72°

(2) 図3は、図1において点AとC、AとD、CとEを結び、線分BEとAC,ADの交点をそれぞれP,Qとし、線分ADとCEの交点をRとしたものです 。図3において、△ABP∼△ADEであることを証明しなさい 。

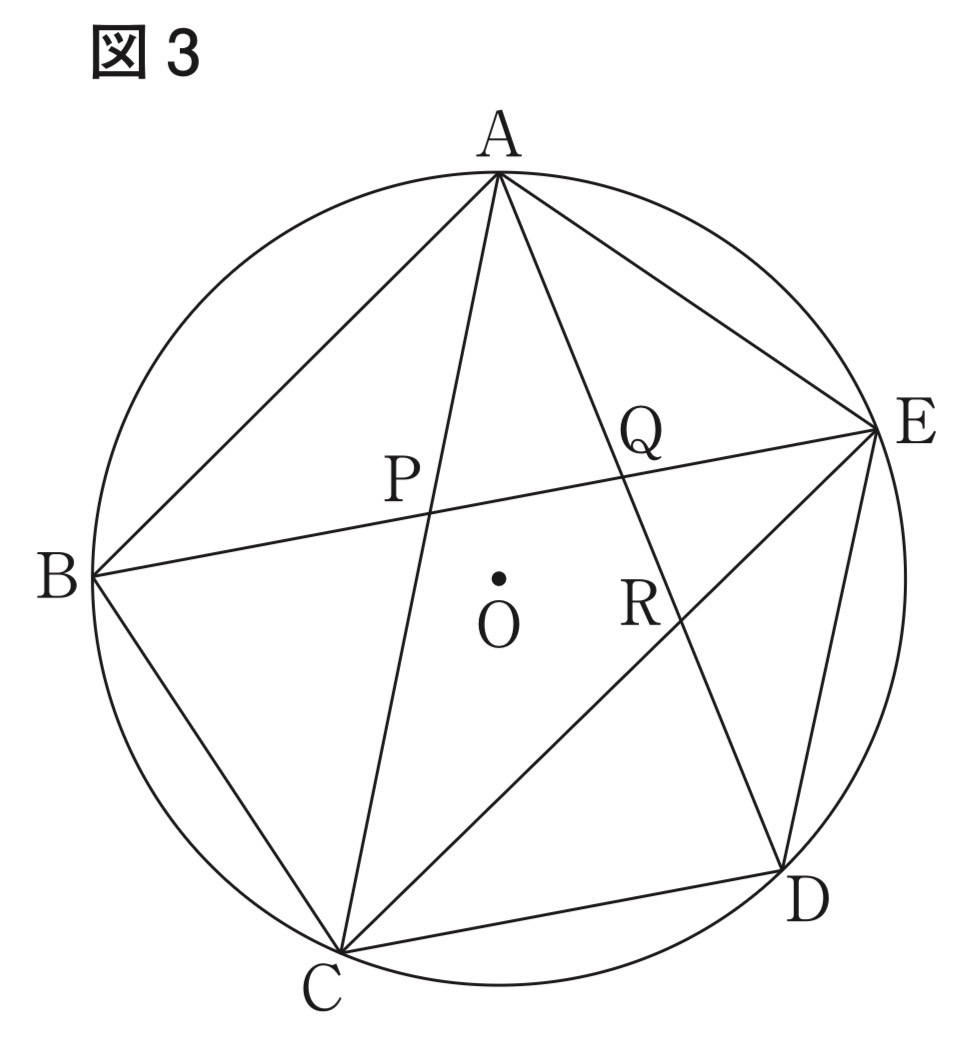
解答 ：（例）△ABP と △ADE において
弧AEに対する円周角は等しいので、
∠ABP=∠ADE ・・・①
弧BCに対する円周角は等しいので、
∠PAB=∠BEC ・・・②
平行線の錯角は等しいので、 BE//CD より、
∠BEC=∠ECD ・・・③
弧DEに対する円周角は等しいので、
∠ECD=∠EAD ・・・④
②、③、④より、
∠PAB=∠EAD・・・⑤
①、⑤より、2組の角がそれぞれ等しいので、
△ABP∼△ADE

解説 ：※模範解答と同様の為省略。

(3) 図4は、図3において、∠EAD=30°、AP:PC=3:2、線分ACが円Oの直径となる場合を表しています 。図4において、AE=6cmのとき、円Oの直径を求めなさい 。

解答 ： 2√21cm

解説 ：






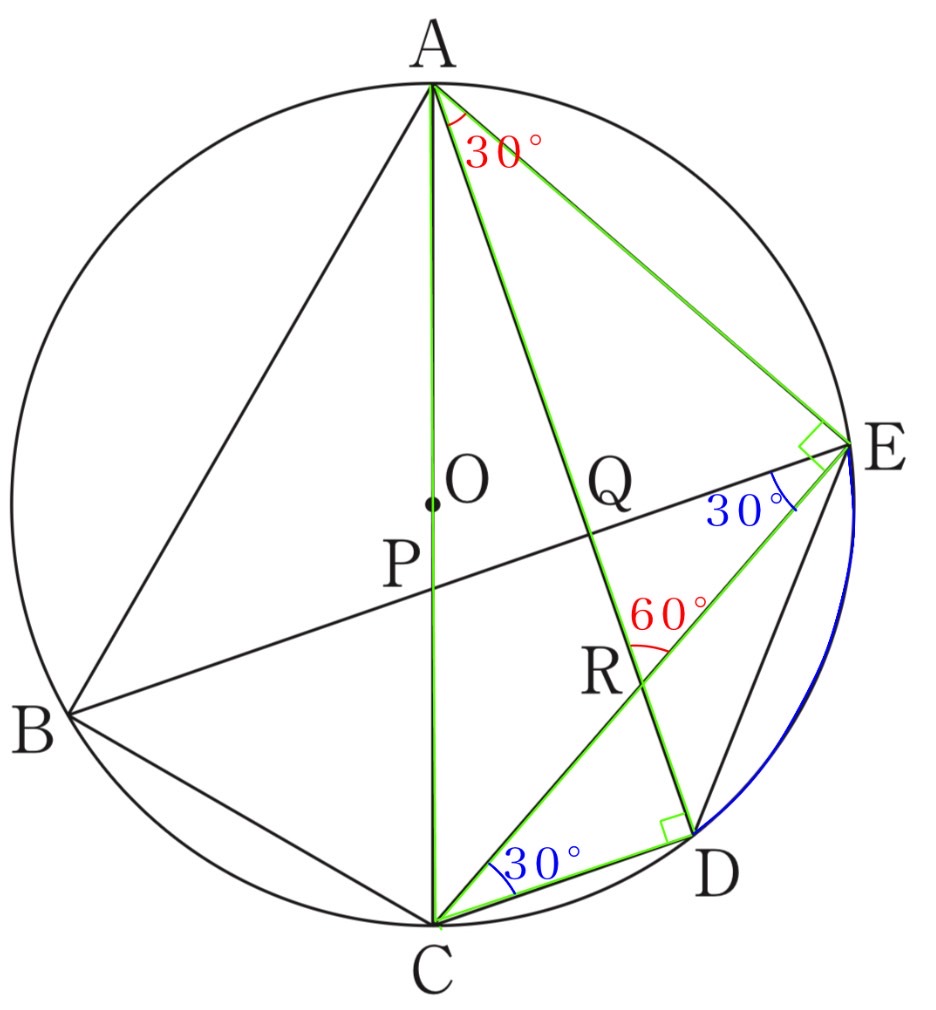
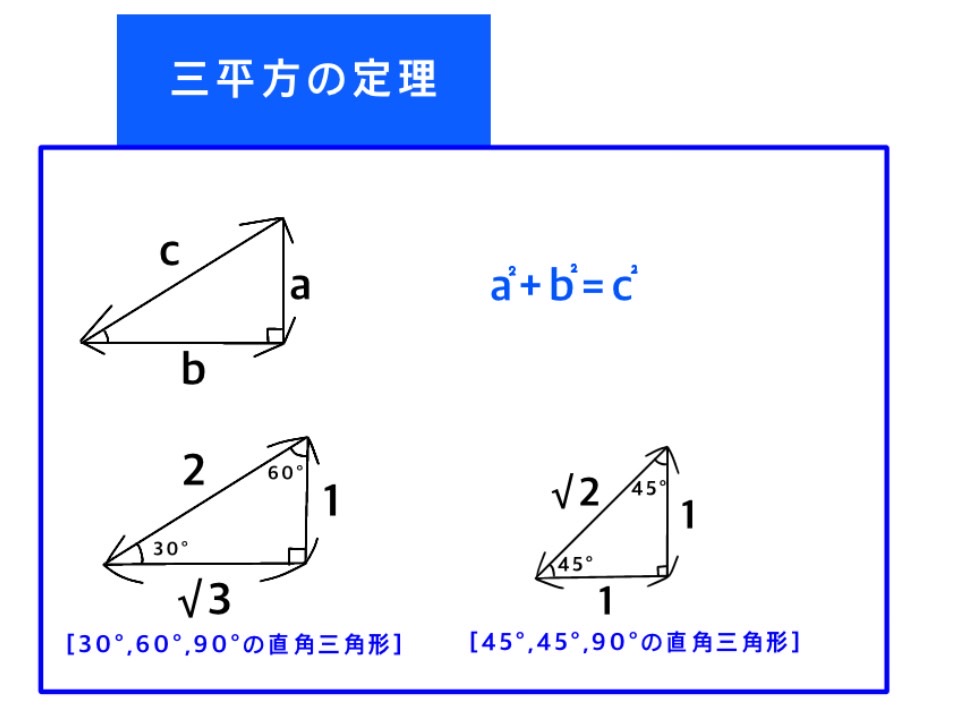
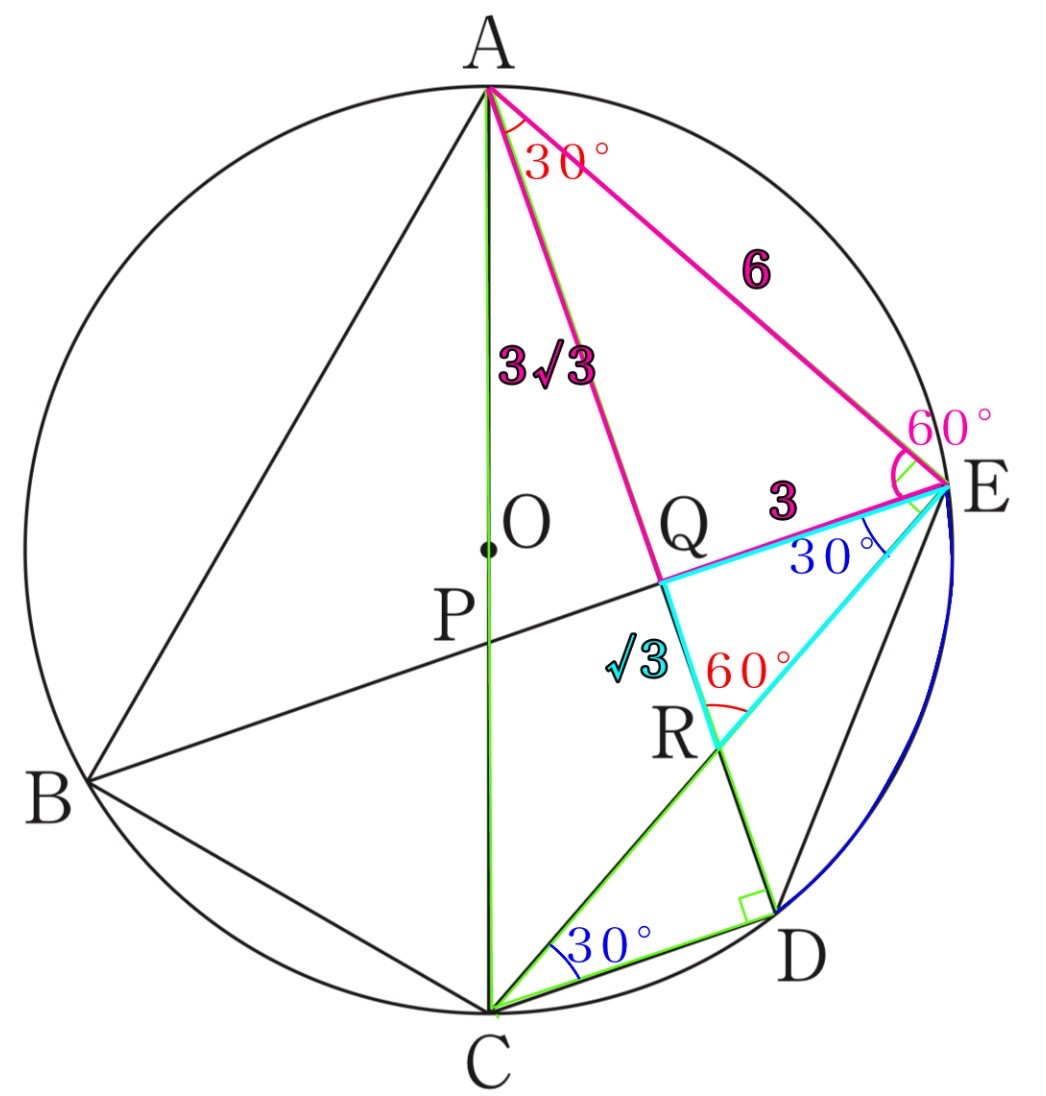
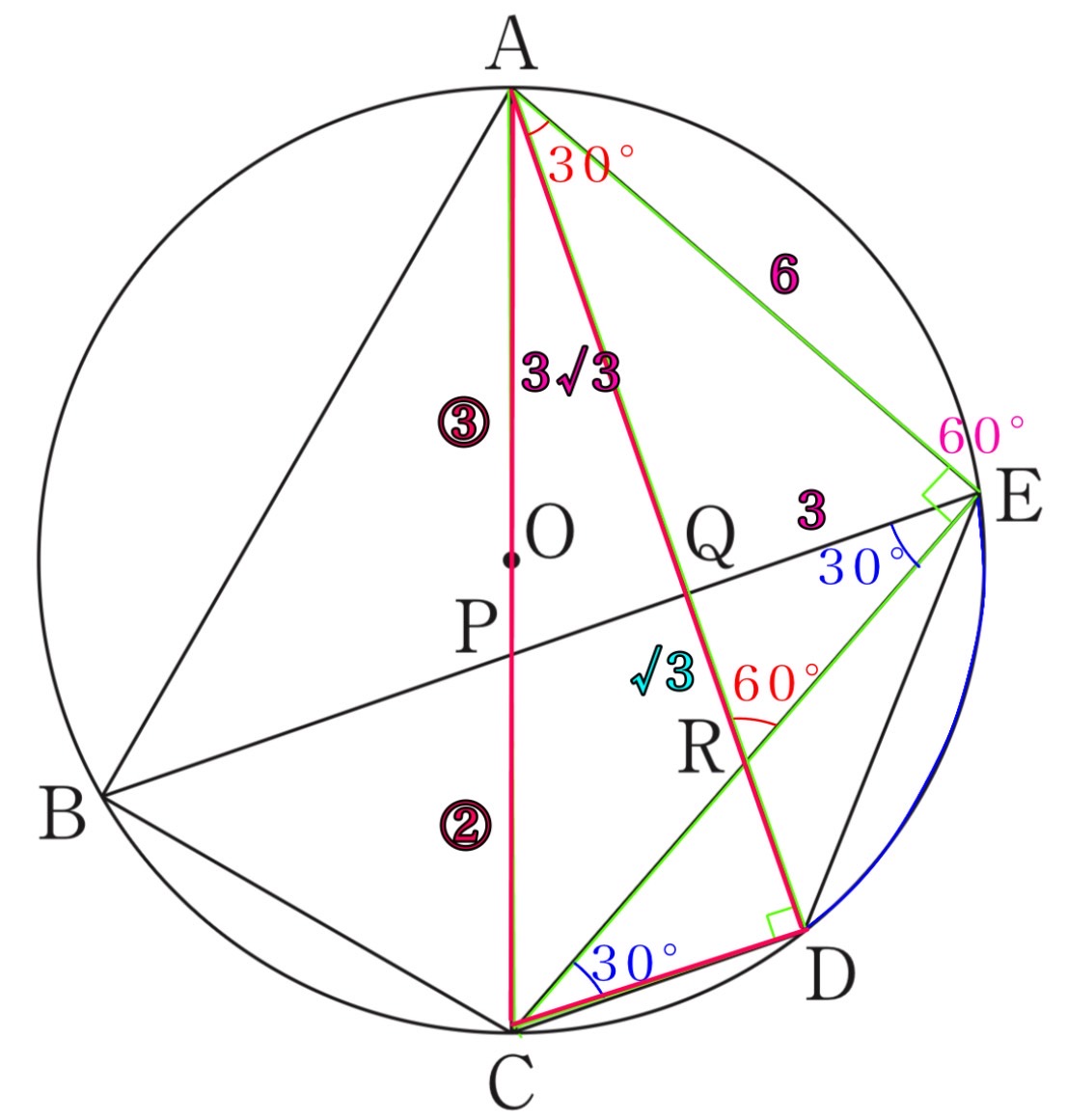
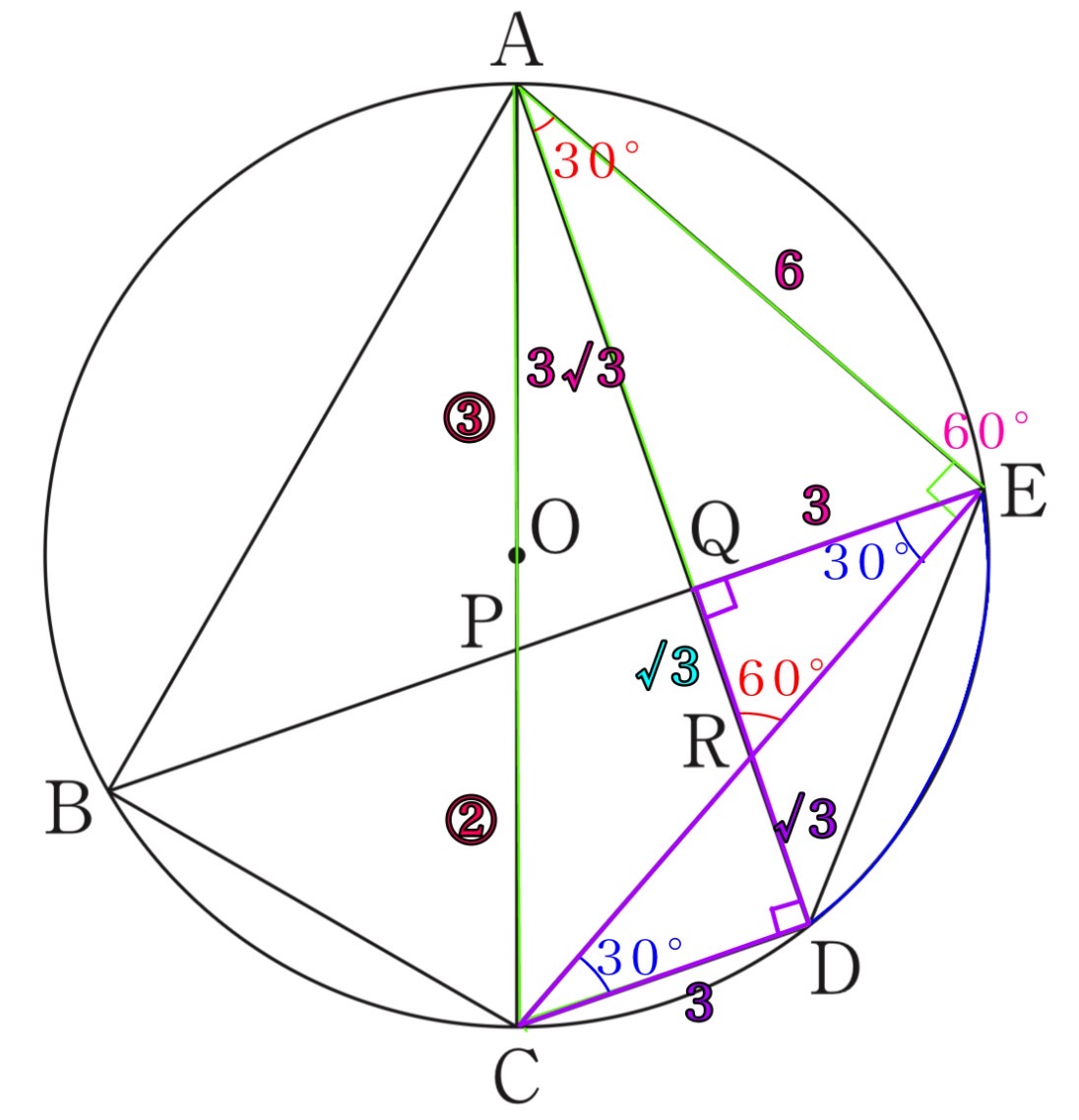
半円の弧に対する円周角で、∠AEC=∠ADC＝90°
∠EAD=30°より、△AREは60°の角を持つ。△AQEは30-60-90の直角三角形なので、
三平方の定理より、
AE:QE:AQ=2:1:√3=6:QE:AQ
QE=3cm,AQ=3√3cm
BE//CDの錯角で∠REQ=30°。弧DEに対する円周角で∠ECD=30°。△CDRも30-60-90の直角三角形。
△APQ∽△ACDよりAQ:QD=AP:PC=3:2だから、
3√3:QD=3:2 → QD=2√3cm
△CDRで三平方の定理よりCD=3cm。
△ACDで三平方の定理より、
[AC]²=[CD]²+[AD]²
[AC]²=3²+ (3√3+2√3)² = 3²+[5√3]²
[AC]²=9+75
[AC]²=84
AC＝2√21cm（円の直径）

■大問６

図1は、底面ABCがAB=4cm、BC=3cm、∠ABC=90°の直角三角形で、側面がすべて長方形の三角柱ABCDEFを表しており、AD=6cmです 。

次の⑴～⑶に答えなさい。

(1) 図1に示す三角柱の展開図として正しいものを、ア～エから選びなさい 。

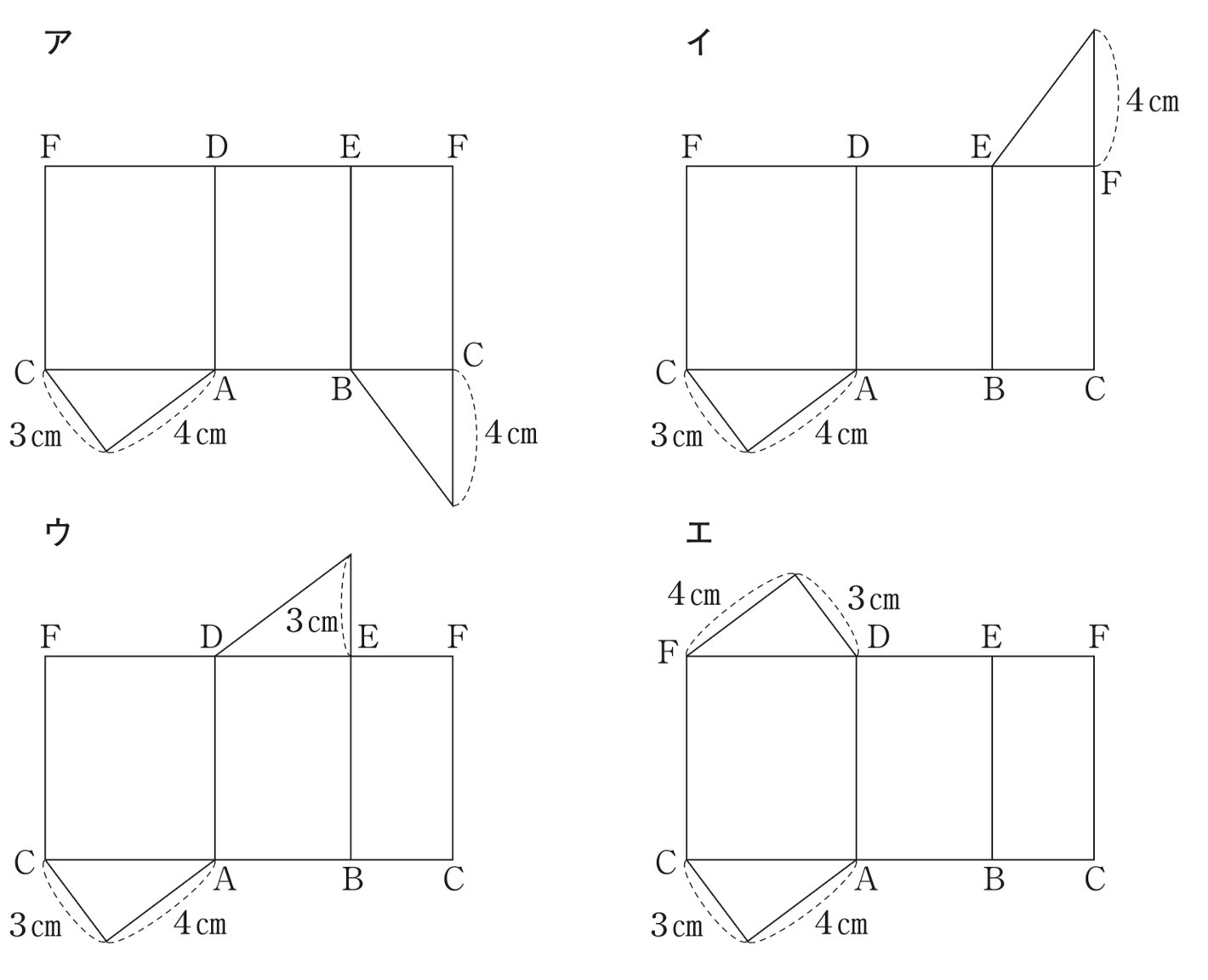
解答 ： ウ

解説 ：底面である天井と床の直角三角形は反対側にあるのでイ～エを選びます。イとエでは、２つの底面の直角三角形が対応していないので間違いです。ウの図を見ると、底面の直角三角形の辺の長さが3cmと4cmで対応しているのでウが適切です。

⑵図1に示す三角柱において辺AB上に点Pを、AP=1cmとなるようにとり、辺CF上に点Qをとる。PQ=5cmのとき、三角錐QABCの体積を求めなさい。

解答 ： 2√7cm³

解説 ：

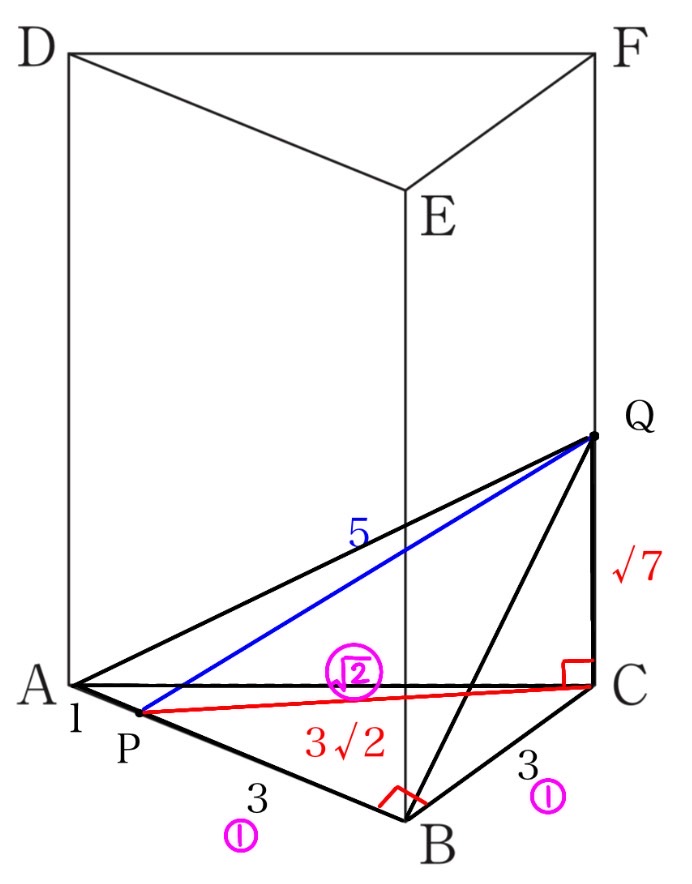
AB=4cm, AP=1cmより、PB=3cmとなります。△PBCは∠PBC=90°の直角三角形なので、三平方の定理よりPC²=PB²+BC²=3²+3²=18。よってPC=3√2cm。次に△PCQは∠PCQ=90°の直角三角形なので、三平方の定理よりPQ²=PC²+QC² → 5²=(3√2)²+QC² → 25=18+QC² → QC²=7。よってQC=√7cm。三角錐QABCの体積は、底面積△ABC × 高さQC × 1/3 で求められます。底面積△ABC = (4×3)/2 = 6cm²。体積 = 6 × √7 × 1/3 = 2√7cm³。

⑶図2は、図1に示す三角柱において、辺DEの中点をMとし、点Mと点A、点Mと点Cを結んだものである。線分MC上に点Kを、KC=ACとなるようにとり、線分MA上に点Lを、LK//ACとなるようにとる。このとき、△LAKの面積は、△MACの面積の何倍か求めなさい。

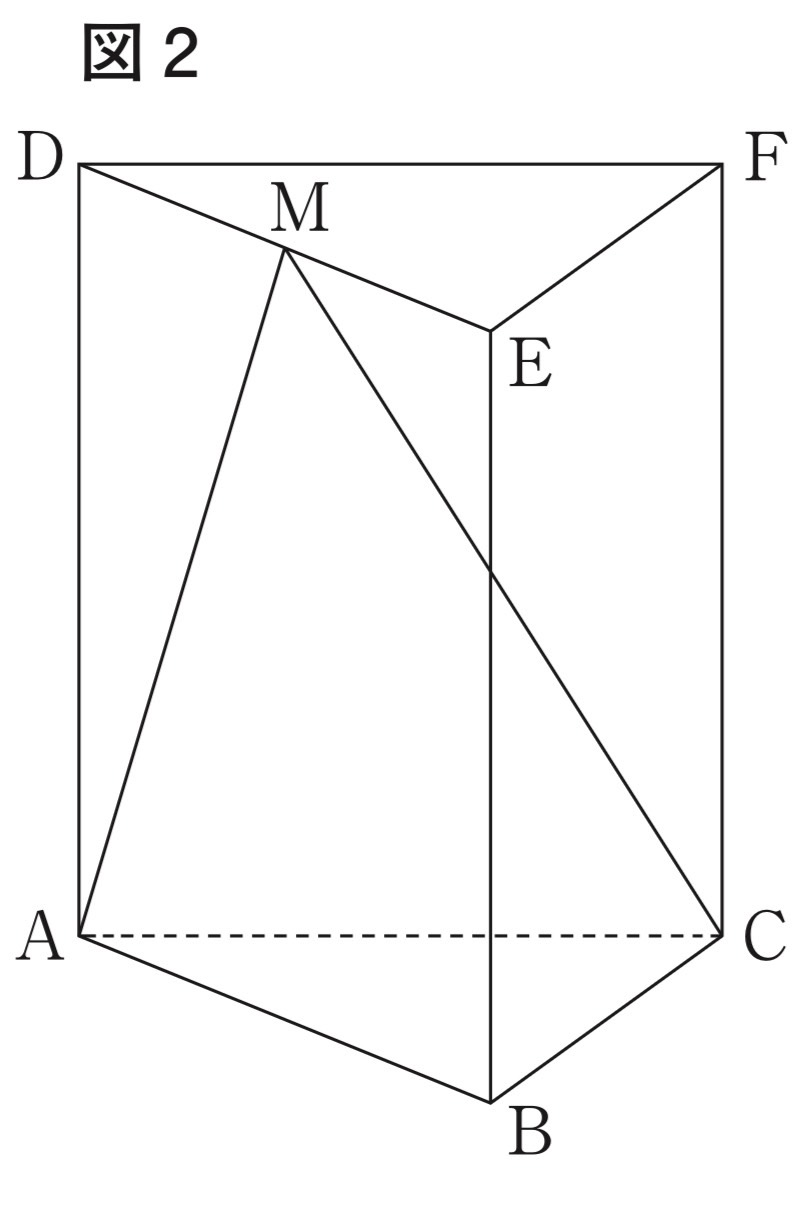
解答 ： 10/49倍

解説 ：


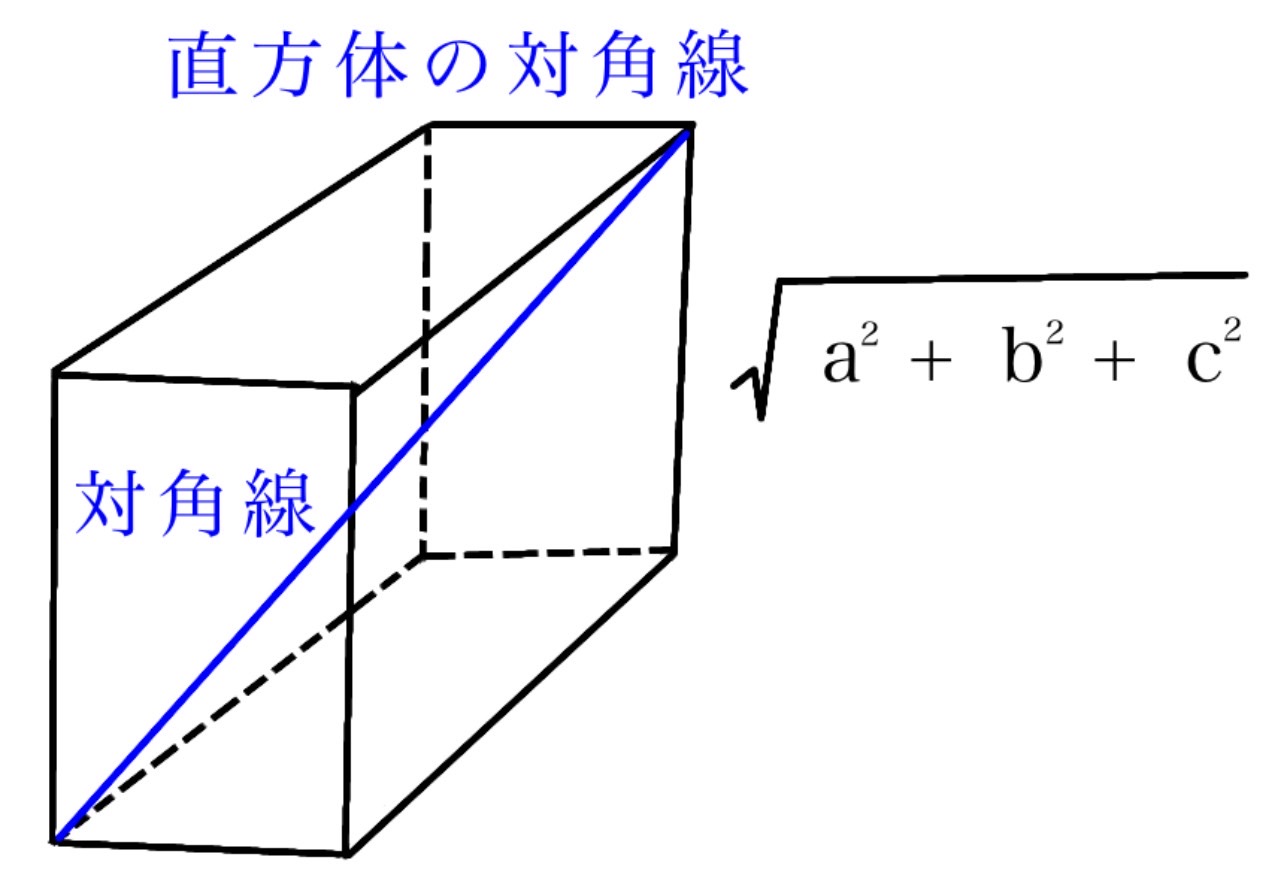
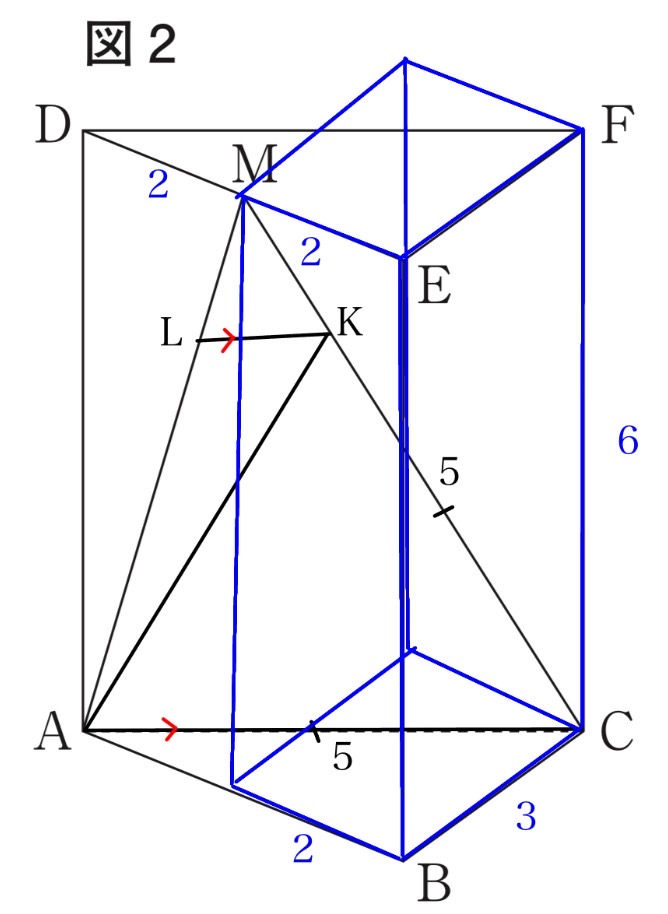
点MはDEの中点なのでEM=2cm。側面CDFEを底面とする直方体を考えると、対角線MCの長さは三平方の定理よりMC = √(CD²+EM²+AD²) = √(3²+2²+6²) = √(9+4+36) = √49 = 7cm。ACの長さは△ABCで三平方の定理よりAC=√(3²+4²)=5cm。条件よりKC=AC=5cmなので、MK = MC – KC = 7 – 5 = 2cm。LK//ACより△MLK∽△MACとなり、相似比はMK:MC=2:7です。よってML:MA=2:7なので、AL=MA-ML=MA(1-2/7)=5/7MA。△LAKの面積と△MACの面積を比較します。頂点Aを共有する△AKCと△AKMの面積比は、底辺の比に等しいので、KC:KM = 5:2です。ここで、△MAC = △AKC + △AKMなので、△AKM = (2/7)△MACです。さらに、△LAKと△MAKは頂点Kを共有するので、面積比は底辺の比AL:AMに等しく、AL:AM = 5:7です。したがって、△LAK = (5/7)△AKM = (5/7) × (2/7)△MAC = (10/49)△MAC。よって10/49倍となります。