2025年度青森学力検査問題過去問【数学】

■問題PDF　

■目次　

■大問１

１-１ア：1 次の(1)~(8) に答えなさい。
(1) 次のア~オを計算しなさい。
ア −11+4

解答 ： -7

解説 ： -11+4=-7

１-１イ：イ 5×{6²+(1−7)}

解答 ： 150

解説 ： 5×{6²+(1−7)}=5(36-6)=5×30=150
※かっこの中から先に計算します。

１-１ウ：ウ (5x²−x+2)−(3x²+x−5)

解答 ： 2x²-2x+7

解説 ： (5x²−x+2)−(3x²+x−5)
まず、はじめにかっこをはずします。
5x²-x+2-3x²-x-5
次に同類項で計算します。
[5-3]x²+[-1-1]x+2-5=2x²-2x+7

１-１エ：エ 12x²y÷(−2x)÷3y

解答 ： -2x

解説 ： 12x²y÷(−2x)÷3y=12x²y÷-6xy=-2x

１-１オ：オ 4/√2+3√8−√18

解答 ： 5√2

解説 ： 4/√2+3√8−√18=4√2/2+3√[2×2×2]-√[2×3×3]=2√2+[3×2]√2-3√2=2√2+6√2-3√2=[2+6-3]√2=5√2

１-２：(2) 画用紙150枚を、おとな9人にa枚ずつ、子ども8人にb枚ずつ配ると、画用紙が余った。このときの数量の関係を、不等式で表しなさい。

解答 ： 9a+8b<150

解説 ： ・大人に配った枚数: 9×a=9a
・子どもに配った枚数: 8×b=8b
・合計枚数: 9a+8b

画用紙が余ったということは、配った枚数が元の画用紙の総数である 150枚よりも少なかったことを意味します。
これらの関係をまとめると、「配った画用紙の合計枚数」が「元の画用紙の総数」より少ない、という不等式が成り立ちます。

配った画用紙の合計枚数<元の画用紙の総数
9a+8b<150

１-３：(3) 右の図は、1つのケースに入ったさくらんぼの重さを 1個ずつ調べ、その結果をヒストグラムに表したものである。例えば、この図から、重さが3g以上5g未満のさくらんぼは3個あったことがわかる。7g以上9g未満の階級の相対度数を求めなさい。
図2

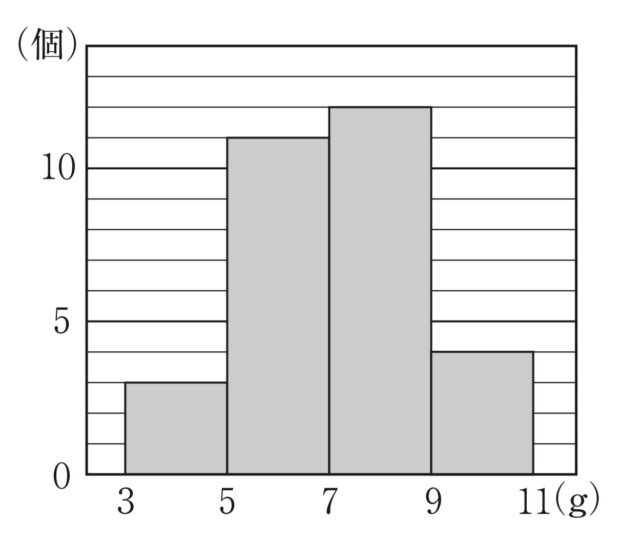
解答 ： 0.4

解説 ： グラフより、
・3g〜5g: 3個
・5g〜7g: 11個
・7g〜9g: 12個
・9g〜11g: 4個
合計: 3+11+12+4=30個

7g〜9gのさくらんぼは 12個 です。
「階級の数」を「全体の数」で割ります。
12÷30=0.4

１-４：(4) 次の方程式を解きなさい。
x²−3x+1=0

解答 ： x=3±√5/2

解説 ： 解の公式

を利用して解きます。
この問題では、a=1,b=−3,c=1 です。これらの値を公式に代入します。
x= -(-3)±√[(-3)²-4⑴⑴]/2⑴=3±√[9-4]/2=3±√5/2

１-５：(5) 5本のうち2本のあたりくじが入っているくじがある。このくじをA、Bの2人がこの順に1本ずつひくとき、2人ともあたりくじをひく確率を求めなさい。ただし、ひいたくじは、もとにもどさないこととする。

解答 ： 1/10

解説 ： あたりをA、Bの順番で引く確率をそれぞれ求めていきます。
・Aが引くとき
全部で5本中、あたりは2本です。
Aがあたりを引く確率は、2/5です。

・Bが引くとき
Aがすでに1本あたりを引いたので、くじは残り4本です。
あたりは残り1本です。
Bがあたりを引く確率は、1/4です。

2人連続で当たる確率は2つの確率をかけ算して解きます。
2/5×1/4=2/20=1/10

１-６：(6) 右の図で、BD = BEである。このとき、∠x の大きさを求めなさい。
図

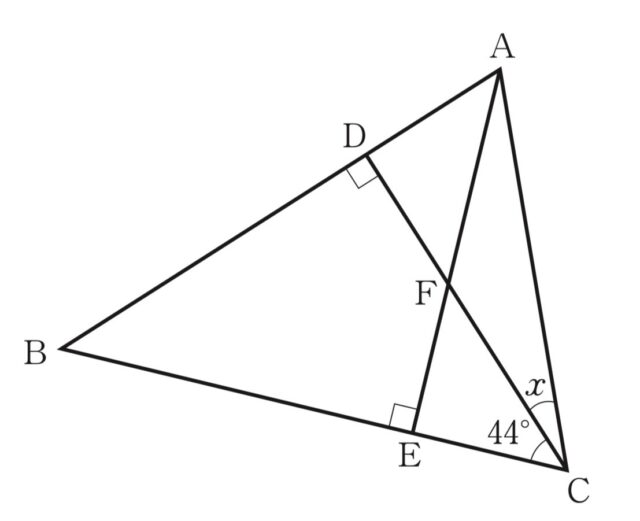
解答 ： 23[度]

解説 ： はじめに、図のように直線ＢＦを引きます。
ＢＤ＝ＢＥ、ＦＤ⊥ＡＢ、ＦＥ⊥ＢＣより、半直線ＢＦは、辺ＡＣの垂直二等分線になります。
このことから、△ＦＡＣは二等辺三角形であることが分かります。
△ＦＣＥの内角と外角の関係より、
∠ＣＦＥ＝∠ＢＥＦ－∠ＥＣＦ＝90°ー44°＝46°

△ＦＡＣの内角と外角の関係より、
ｘ＋ｘ＝46°
ｘ＝23°
図

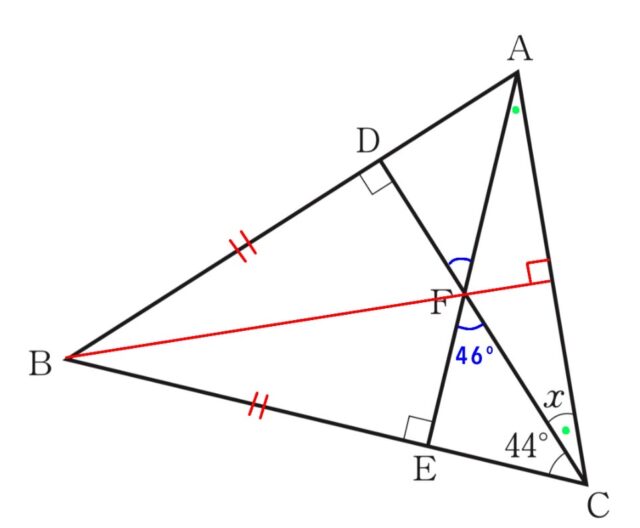
１-７：(7) 硬貨を1枚投げるとき、表と裏の出方について述べた文として適切でないものを、次のア〜エの中から1つ選び、その記号を書きなさい。ただし、表と裏の出方は同様に確からしいものとする。
ア 10回続けて投げると、表が3回出る場合がある。
イ 20回続けて投げると、表と裏が10回ずつ出る。
ウ 2000回続けて投げると、表と裏がおよそ1000回ずつ出ると予想できる。
エ 投げる回数が多いほど、表の出る相対度数のばらつきは小さくなり、その値は0.5に近づく。

解答 ： イ

解説 ： ア：10回中3回表が出るのは、起こりうる結果の一つです。→○
イ：20回中10回ずつ出るのは、あくまで最も確率の高い結果であり、必ずそうなるわけではありません。→×
ウ：2000回のように回数が多くなると、大数の法則により、結果は理論上の確率に近づくため、表と裏がおよそ1000回ずつ出ると予想できます。→○
エ：投げる回数が多くなるほど、表の出る相対度数（表の出た回数 ÷ 全体の回数）のばらつきは小さくなり、その値は理論上の確率である0.5に近づいていきます。→○

１-８：(8) 家から24km離れた図書館へ、自動車で一定の速さで向かった。右の図は、出発してからx分後の家からの道のりをykmとして、図書館に着くまでのxとyの関係を表したグラフである。家から18kmの地点を通過したのは、家を出発してから何分何秒後か。求めなさい。
図

解答 ： 22[分]30[秒後]

解説 ： x分後の道のりをykmとすると、グラフは原点を通る直線なので、xとyは比例の関係にあります。
y=ax
グラフから、x=30のときy=24なので、
24=a×30
a=24/30=4/5
よって、式は y=(4/5)x となります。
y = 18km のときのxの値を求めると、
18=(4/5)x
x=18×(5/4)=90/4=22.5
22.5分 = 22分30秒
したがって、答えは22分30秒後です。

■大問２

２-１：2 次の(1), (2) に答えなさい。
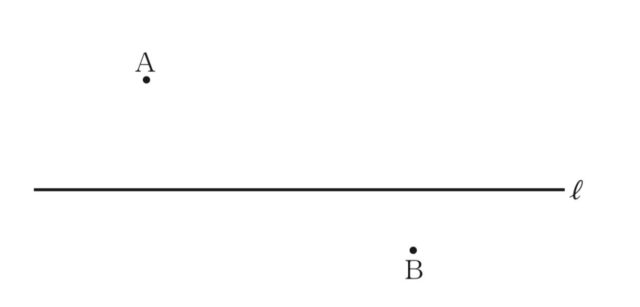
(1) 下の図において、直線l上に、2点A. Bを通る円の中心Oを作図によって求めなさい。
ただし、作図に使った線は消さないこと。
図

解答 ：

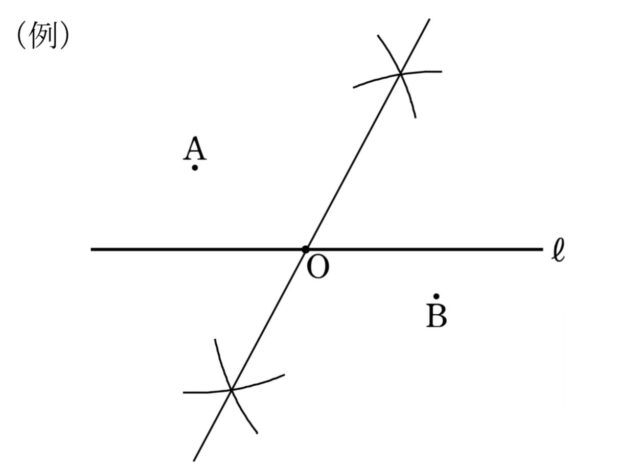
解説 ： 2点A, Bを通る円の中心Oは、線分ABの垂直二等分線上にあります。また、中心Oは直線ℓ上にもあります。
したがって、中心Oは、線分ABの垂直二等分線と直線ℓの交点になります。

手順1:コンパスを使って、点Aと点Bを中心とする円弧を描きます。
点Aを中心とし、線分ABの長さの半分より長い半径で円弧を描きます。
同じ半径で、点Bを中心として円弧を描きます。

手順2:2つの円弧の交点を通る直線を引きます。
この直線が線分ABの垂直二等分線です。

手順3:垂直二等分線と直線ℓの交点が中心Oです。
2つの直線の交点をOとします。
図

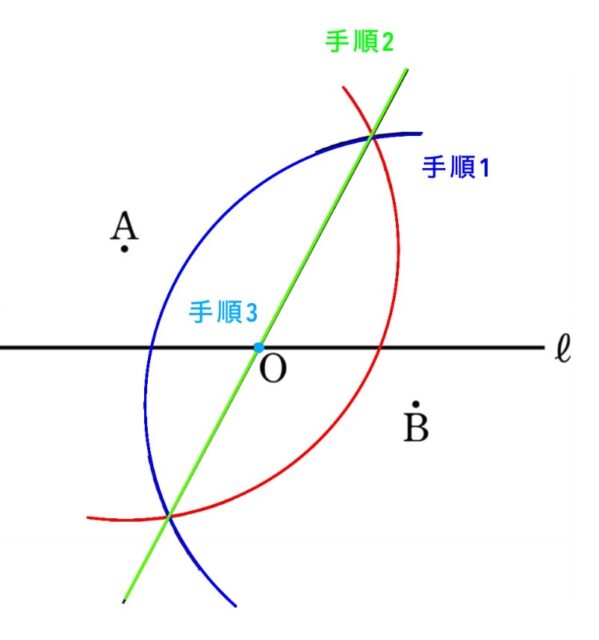
２-２：(2) 右の図は、ある月のカレンダーである。このカレンダーで、右のように縦3つ、横2つの数を□で囲んだ。
次の文章は、□の中の4すみの数のうち、斜めの関係にある2つの数の積には、どのような性質があるのかを調べているレンさんとメイさんの会話である。あ〜えにあてはまる式をそれぞれ書きなさい。
図

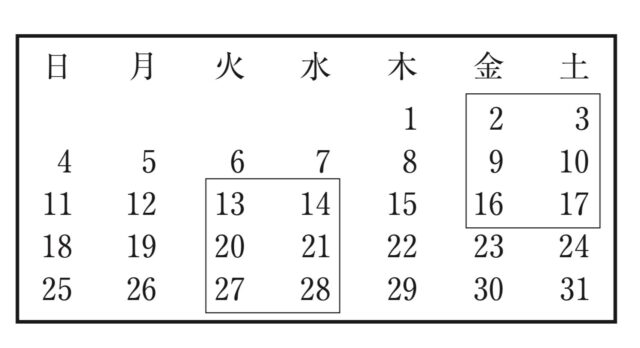
レン: 例えば、図1、2で考えると4すみの数のうち、斜めの関係にある2つの数の積をそれぞれP、Qとすると、
P=3×16=48 と Q=2×17=34
P=14×27=378 とQ=13×28=364
となるね。
図1

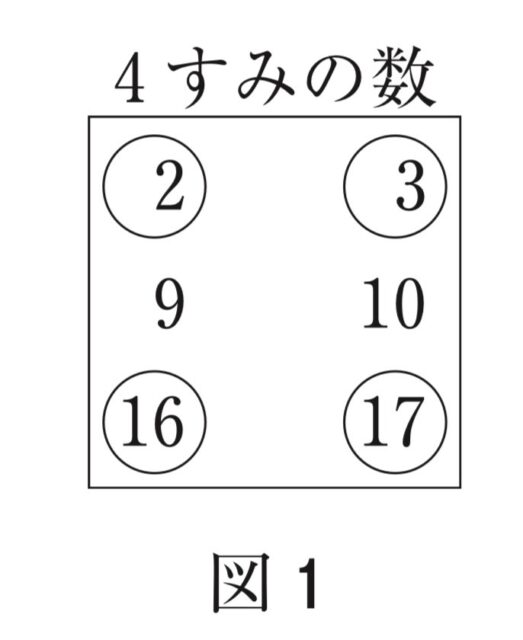
図2

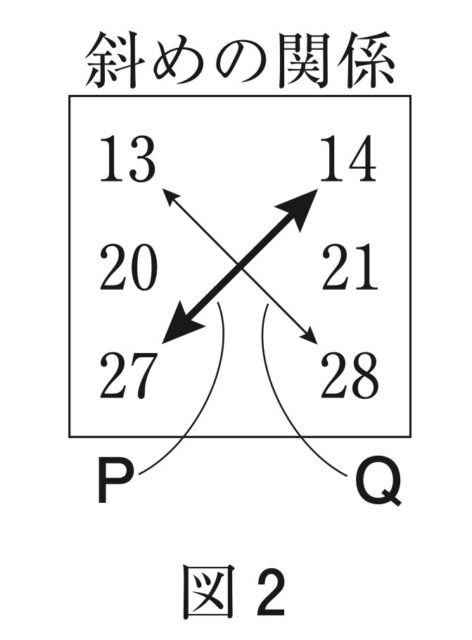
2つとも、 P−Q=14 になったけど
カレンダーの他の場所を、同じように□で囲んでもP-Q=14になるのかな。
メイ:いつでも成り立つかどうかは、文字を使って説明する必要があるね。
レン: 4すみの数のうち、一番小さい自然数をnとすると残りの3つの自然数は小さい順に[あ]、[い]、[う]と表すことができるよ。
メイ:そうか。nを使った式で、P-Qの値を表してみるよ。
([あ])×([い])-n×([う])
=([え]+14)-([え])
=14
このことから、カレンダーで、縦3つ、横2つの数を□で囲んだ4すみの数のうち、
斜めの関係にある2つの数の積は、いつでも P−Q=14 になるといえるね。

解答 ： あ：n+1　い：n+14　う：n+15　え：n²+15n

解説 ： □で囲まれた4つの数のうち、一番小さい数を n とします。
4すみの数は、一番小さい数から順に n, n+1, n+14, n+15 となります。
左上：n
右上：n+1
左下：n+14
右下：n+15

(あ)×(い)−n×(う)
=(n+1)×(n+14)−n×(n+15)
=(n²+15n+14)−(n²+15n)
=(n²+15n)+14−(n²+15n)

あ：n+1、い：n+14、う：n+15、え：n²+15n

■大問３

３-１ア：3 次の(1), (2) に答えなさい。
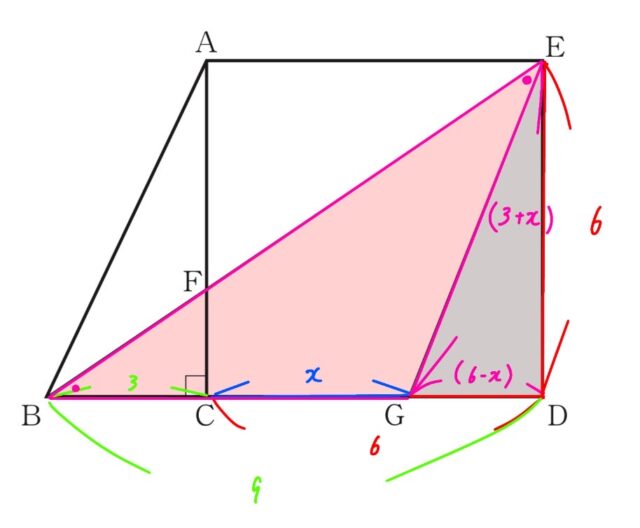
(1) 下の図の△ABCは ∠C=90°の直角三角形であり、四角形ACDEは辺ACを1辺とする正方形である。辺ACと線分BEとの交点をFとし、辺CD上に ∠AEB=∠BEG となる点Gをとる。このとき、次のア、イに答えなさい。

ア △AFEと△DEBが相似になることを証明しなさい。
図

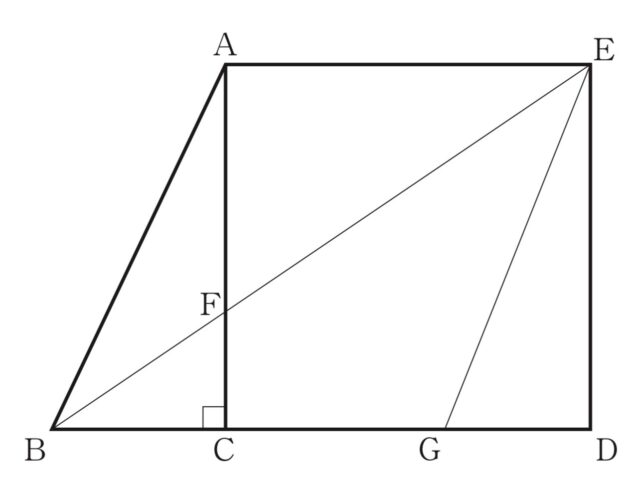
解答 ： （例）△AFEと△DEBにおいて
仮定より
∠FAE=∠EDB…①
また、AE//BDより、錯角は等しいから
∠AEF=∠DBE…②
①、②より
2組の角がそれぞれ等しいので
△AFE∽△DEB

解説 ： ★三角形の相似条件
①三組の辺の比がそれぞれ等しい
②二組の辺の比とその間の角がそれぞれ等しい
③二組の角がそれぞれ等しい

証明では上記の相似条件を見つけましょう。
下の図はその際の参考図です。
図

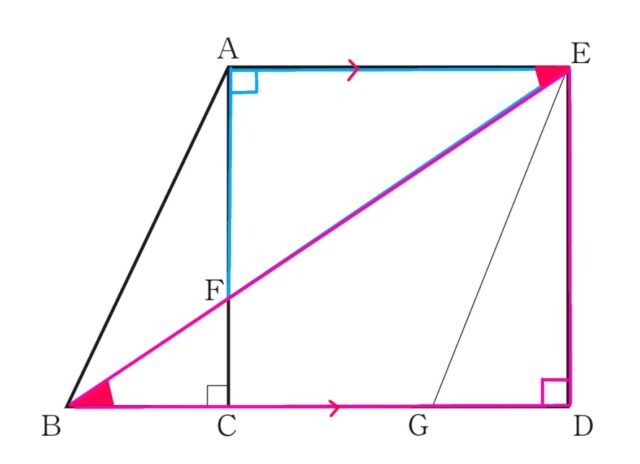
３-１イ：イ AC=6 cm, BD=9 cmのとき、次の(ア) (イ)に答えなさい。
(ア) 線分AFの長さを求めなさい。
(イ) 線分CGの長さを求めなさい。

解答 ： ア：4[cm]　イ：7/2[cm]

解説 ： (ア)AC＝６cmより、AE=DE=6cm
△AFE∽△DEBより、
対応する辺の比は等しいから、
AE:DB=AF:DE
6:9=AF:6
2:3=AF:6
AF=4cm

(イ)
線分CGの長さをxcmとします。
BC=BD-CD=9-6=3cm
BG=BC+CG=(3+x)cm
問題文より、∠AEB=∠BEG=∠GBEなので△GBEは二等辺三角形になるので、
EG=BG=(3+x)cm
GD=CD-CG=(6-x)cm
三平方の定理より、
EG²=GD²+DE²
(3+x)²=(6-x)²+6²
9+6x+x²=36-12x+x²+36
18x=63
x=7/2cm
図

３-２ア：(2)
図1は、三角柱であり、 ∠ABC=90°, AB=5cm,AD=BC=10cmとする。次のア、イに答えなさい。
ア 辺ADと垂直な面をすべて書きなさい。
図

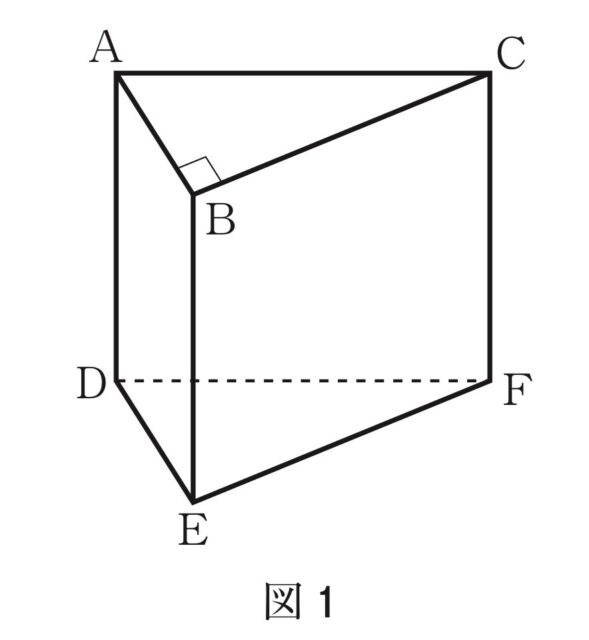
解答 ： 面ABC,面DEF

解説 ： 三角柱は、側面が底面に対して垂直に立っているため、辺ADは底面のどの辺とも垂直になります。したがって、辺ADは底面全体（面ABCと面DEF）に垂直です。

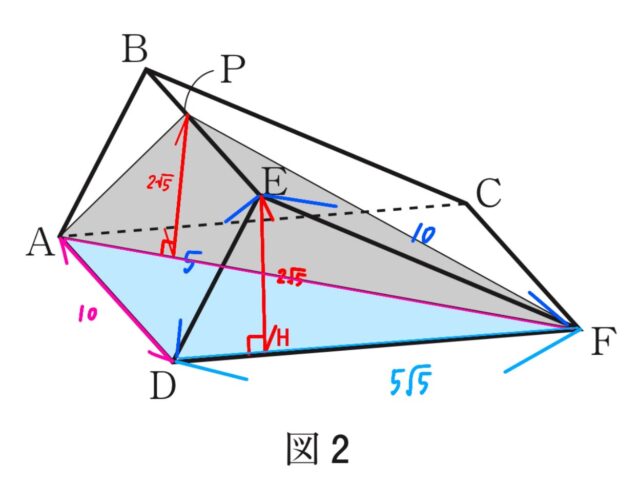
３-２イ：イ 図2は、図1の三角柱を、面ADFCが底面となるように置いたものである。辺BE上に点Pをとり、3点P, A, Fを結んでできる△PAFと面ADFC が垂直になるとき、△PAFの面積を求めなさい。
図

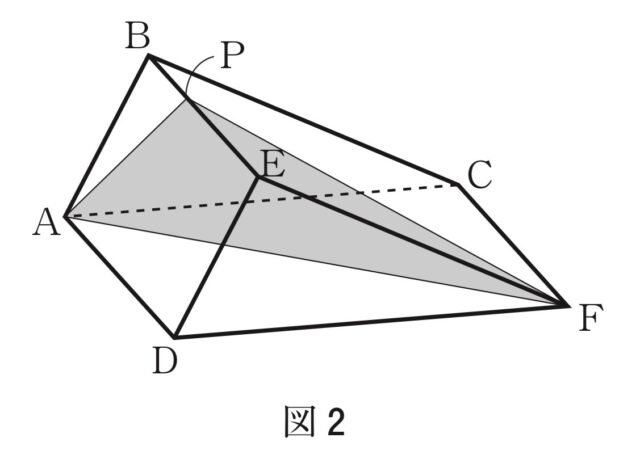
解答 ： 15√5[cm²]

解説 ： AB=DE=5cm
BC=EF=10cm
∠DEF=90°
以上から、三平方の定理より、
DE²=DE²+EF²
DF²=5²+10²
DF²=125
DF=5√5cm(DF>0)
Eからの垂線と辺DFとの交点をHとします。
△DEF
=DE×EF×1/2
=5×10×1/2=25cm²…①
△DEF
=DF×EH×1/2
=5√5×EH×1/2
=5√5EH/2cm²…②
①＝②より、
5√5EH/2=25
EH=2√5cm
よって、△PAFの高さは2√5cm…③
図

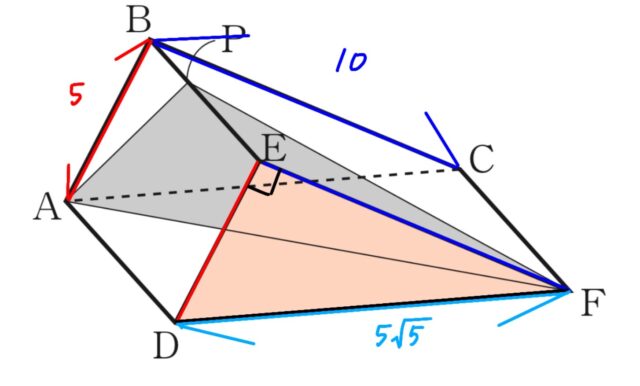
△ADFで、三平方の定理より、
AF²=AD²+DF²
AF²=10²+(5√5)²
AF²=225
AF=15cm(AF>0)…④
③、④より、△PAFの面積は、
15×2√5×1/2
=15√5cm²
図

■大問４

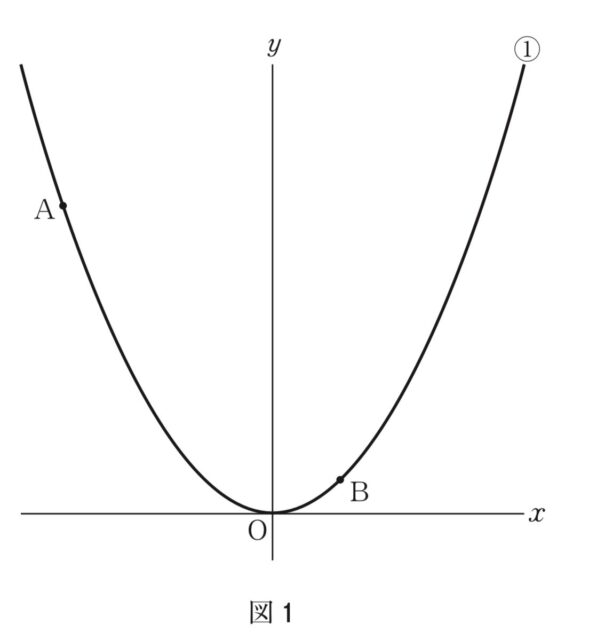
４-１：4 図1で、①は関数 y= 1/4x²のグラフであり、2点A, Bは①上の点でx座標がそれぞれ-6,2である。次の (1)〜(3) に答えなさい。ただし、座標軸の単位の長さを1cmとする。
(1) ①の関数について、xの変域が −6≤x≤2のときのyの変域を求めなさい。
図1

解答 ： 0≦y≦9

解説 ： y=1/4 x²のグラフは、一番下が原点 (0, 0) にあるU字型の放物線です。
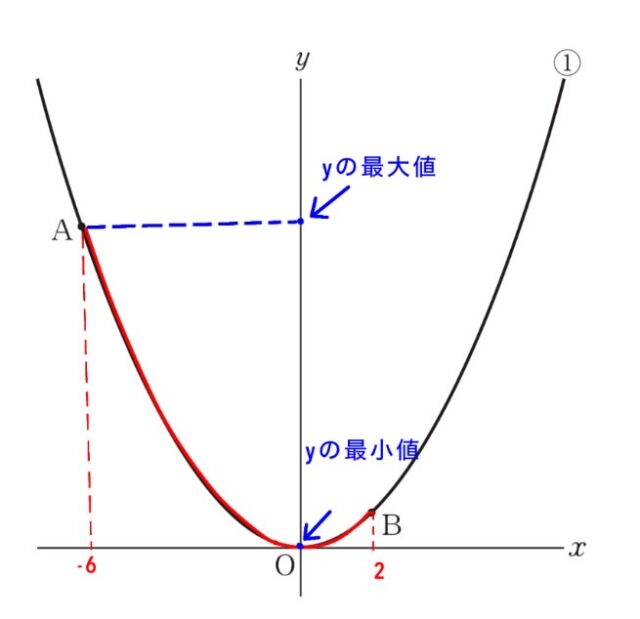
x の範囲が −6 から 2 までなので、この区間のグラフで一番低い点はx=0 で、y=0 です。
一番高い点は、図よりx=-6のときです。
x=−6 のとき: y=1/4(−6)² =1/4×36=9
よってy の最大値は 9 です。
したがって、求めるyの変域は0≦y≦9です。
図

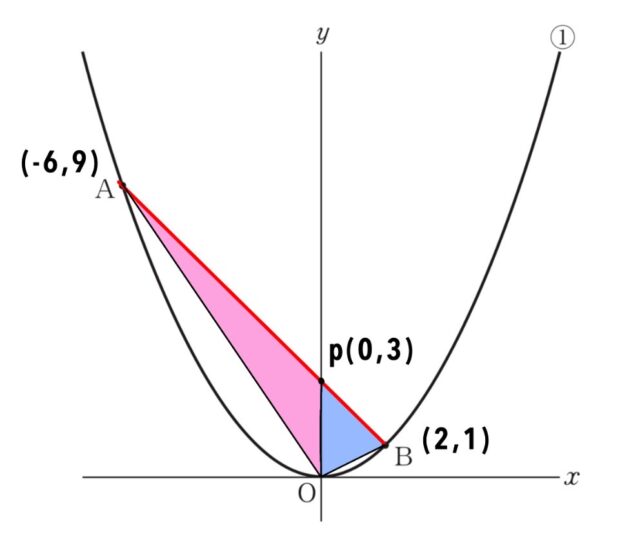
４-２：(2) △AOBの面積を求めなさい。

解答 ： 12[cm²]

解説 ： 点Aと点Bの座標はそれぞれ、
点A:y=1/4(-6)²=1/4×36=9
点B:y=1/4(2)²=1/4×4=1
よって、A(-6,9)、B(2,1)　となります。
ここから、直線ABを求めていきます。
変化の割合=yの増加量/xの増加量でもとめることができるので、
xの増加量=2-(-6)=8
yの増加量=1-9=-8
変化の割合=-8/8=-1
直線ABはy=-1x+bとなり、これに(2,1)を代入します。
直線AB 1=-2+b
b=3
直線AB y=-2+3となり、y軸との交点をp(0,3)と置きます。
△AOB=△AOP+△BOP
△AOP=3×6/2=9
△BOP=3×2/2=3
△AOB=9+3=12cm²
図

４-３ア：(3) 図2は、図1に②をかき加えたもので、②は点Bを通り、傾きが負の直線である。②と①の交点で、点Bとは異なる点をP, ②とx軸との交点をQとし、点Pのx座標をtとする。また、点Pからx軸にひいた垂線とx軸との交点をHとする。このとき、次のア、イに答えなさい。
図2

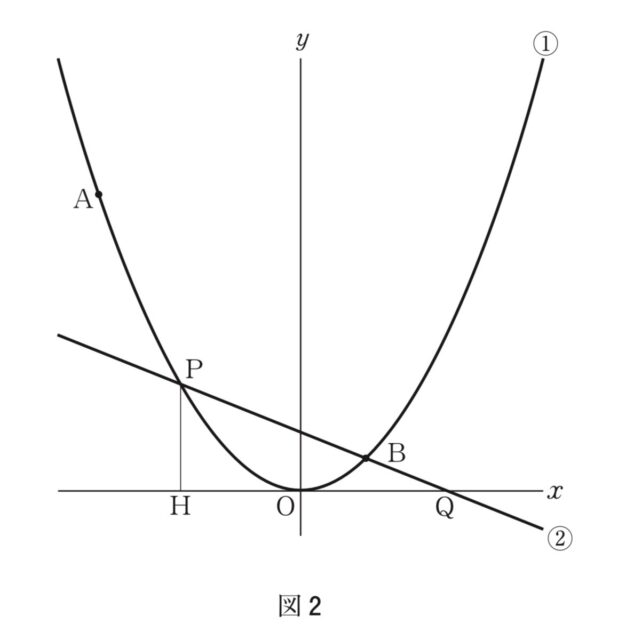
ア t=−4 のとき、直線②の傾きを求めなさい。

解答 ： -1/2

解説 ： 点P: x座標はt=−4。放物線①上の点なので、y=1/4 (−4)²=1/4×16=4。
よって、点Pの座標は (−4, 4)です。
点Bの座標は (2, 1) です。
xの増加量は、-4-2=-6。
yの増加量は、4-1=3。
傾き = 3/-6=-1/2

４-３イ：イ QH=4PH のとき、tの値を求めなさい。

解答 ：-3

解説 ： 点Pの座標は、点Ｐは①上の点より、
y=1/4t²
点P(t,1/4t²) です。
よって、PH=1/4 t²cmです。
問題文より、QH=4PHなので、
QH=1/4 t²×4=t²
よって、Qのx座標は、t+t² です。
直線PQの式を求めると、
点P(t,1/4 t²)
点Q(t+t²,0)
xの増加量:t+t²-t=t²　
yの増加量:0-1/4t²=-1/4 t²　
傾き=-1/4 t² /t²=-1/4
直線PQ y=-1/4 x+b
y=-1/4 x+bに(2,1)を代入します。
1=-1/4×2+b
1=-1/2+b
b=1+1/2
b=3/2
したがって、直線PQは、y=-1/4 x+3/2 となります。
直線PQに（t+t²,0）を代入します。
0=-1/4(t+t²)+3/2
0=-1/4 t+-1/4 t²+3/2
0=t²+t-6
(t+3)(t-2)=0
t<0より、t=-3

■大問５

５-１：5 〔練習〕は、マユさんのノートの一部である。次の(1), (2) に答えなさい。
〔練習〕下の図で、線分BHと線分AHの長さを求めなさい。
図

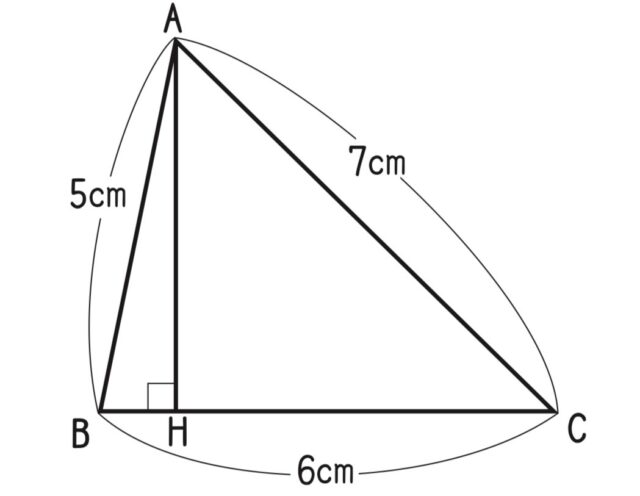
BH=x cmとすると、CH=(6−x) cmとなる。
AH=h cmとすると、三平方の定理より
h²=5²−x²…①
h²=7²−(6−x)²…②
①、②より
「5² −x²=7²−(6−x)²
25−49=36−12x」
12x=60
x=5
また、
(1) 図1で、線分 BHの長さを求める計算は間違っているところがある。「」の部分でどのような間違いがあるのかを説明しなさい。また、線分AHの長さを求めなさい。

解答 ： 間違いの説明：（例）かっこをはずすときに、36と-12xの符号を変えていない。
線分AH：2√6[cm]

解説 ： [正しい計算]
5² −x²=7²−(6−x)²
25-x²=49-(36-12x+x²)
25-x²=49-36+12x-x²
25-49=-36+12x
12x=25-49+36
12x=12
x=1
①の式に代入すると、
h²=5²−1².
h²=24
h=2√6cm
よって、AH=２√6cm

５-２ア：(2) 〔練習]のあと、先生から 「△ABCの条件を変えて、問題を作成してください」と指示された。図2は、生徒が作成した問題の一部である。作成した 【問題】 について話している先生と生徒のやりとりを読んで、次のア〜エに答えなさい。先生: リクさんが 【問題】を作る上で、工夫したことを教えてください。
図2

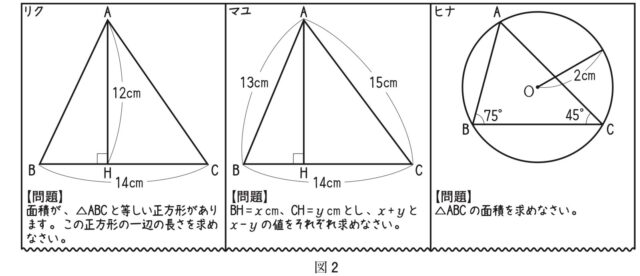
リク: 平方根の学習で、正方形の面積から1辺の長さを求め、素因数分解を使って根号の中を簡単な数で表すことを学んだので、それを活用したいと思いました。
先生: マユさんとヒナさんは、どのように考えて 【問題】を作ったのですか。
マユ: BH = x cm. CH=y cmとおいて、2つの文字を使って等式を作ることができないかと考えたところ、x+yとx−yの値をそれぞれ求められることに気づきました。
ヒナ:円周角の定理と特別な直角三角形の辺の比を使って、面積を求める問題を作りたいと考えました。まず、辺BCの長さは〔〕cmだとわかります。そして、補助線を1本追加することで、△ABCの底辺と高さを見いだし、面積を求めることができます。

ア リクさんの 【問題】で、△ABCの面積を素因数分解した形で表しなさい。

解答 ： 2²×3×7

解説 ： リクさんの【問題】は、底辺BCが14cm、高さAHが12cmの三角形です。
三角形の面積の公式は「底辺 × 高さ ÷ 2」なので、△ABCの面積は以下の通りです。
面積 = 14×12÷2=84
図

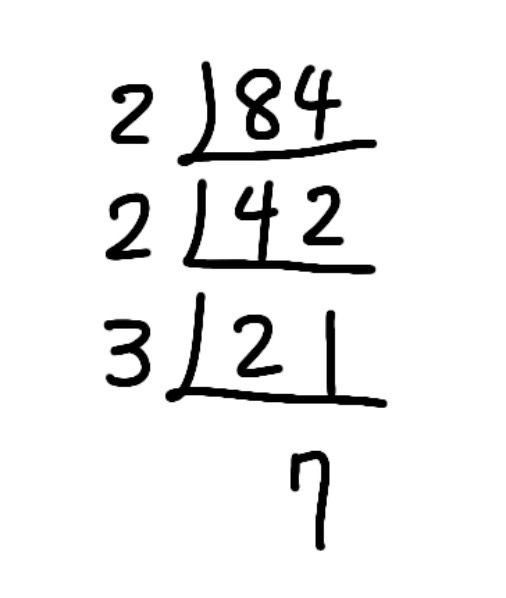
したがって、△ABCの面積を素因数分解した形は 2²×3×7 です。

５-２イ：イ マユさんの 【問題】で、x−yの値を求めなさい。

解答 ： -4

解説 ： マユさんの【問題】では、BH=x cm、CH=y cm、BC=14cmです。
したがって、x+y=14 という関係が成り立ちます。
また、直角三角形ABHとACHにおいて、三平方の定理より、
AH²=13²−x²=169−x²
AH² =15²−y²=225−y²
169−x²=225−y²
y²−x²=225−169
y²−x²=56
(y+x)(y−x)=56
x+y=14を代入すると、
14(y−x)=56
y−x= 56/14=4
したがって、x−y の値は −4 です。

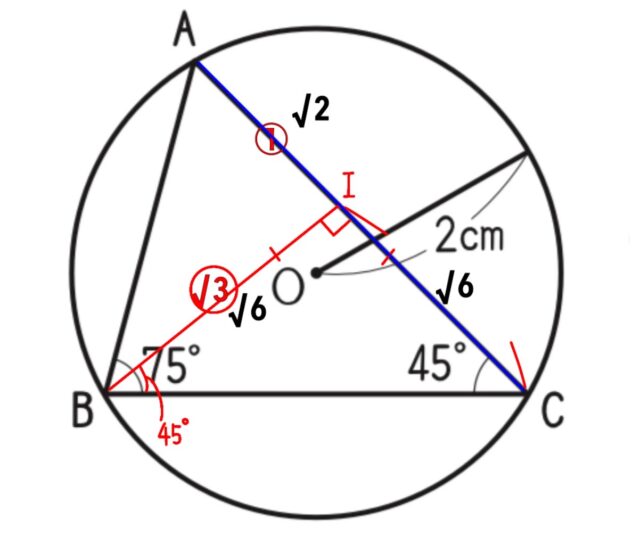
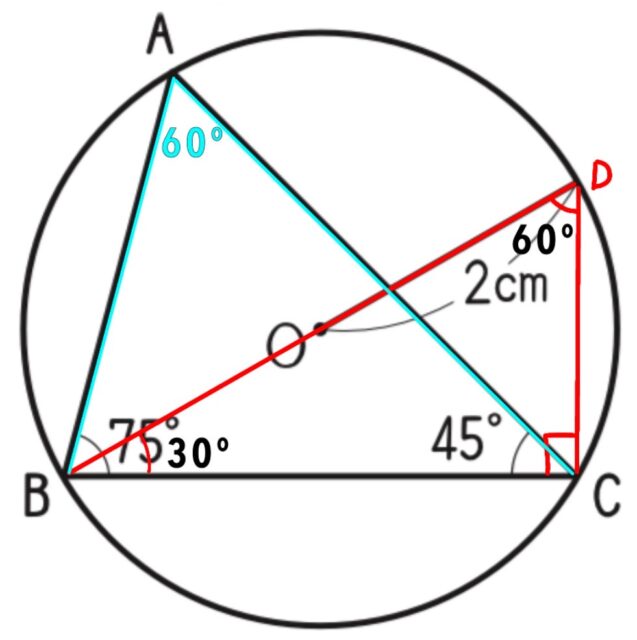
５-２ウ：ウ 〔〕にあてはまる数を書きなさい。

解答 ： 2√3

解説 ： CDに補助線を引きます。
△ABCより、∠BAC=180°-(75°+45°)=60°
∠BDCは、弧BCに対する円周角だから、
∠BAC=∠BDC=60°
また、直径BDに対する円周角だから、
∠BCD=90°
△DBCで、直角三角形の辺の比より、
BD:BC=2:√3
4cm:BC=2:√3
BC=2√3cm

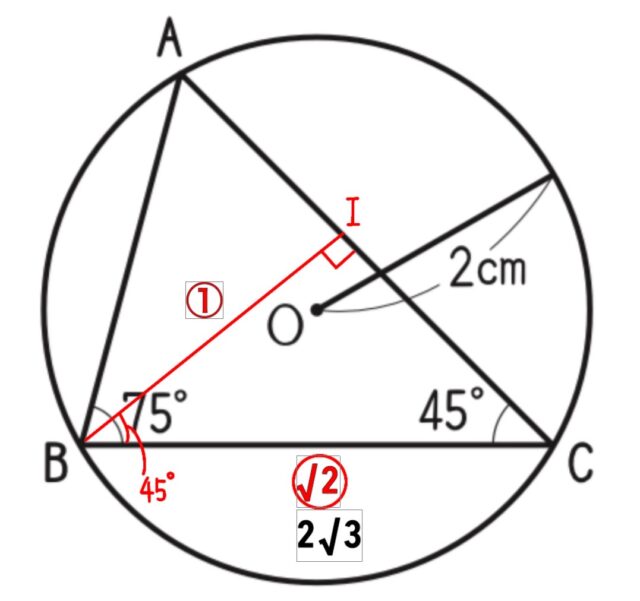
５-２エ：エ ヒナさんの 【問題】を解きなさい。

解答 ： 3+√3[cm²]

解説 ： Ｂからの垂線とＡＣとの交点をＩとします。
∠IBC=∠ICB=45°
△IBCは直角二等辺三角形の辺の比より、
IB:BC=1+√2
IB:2√3=1:√2
IB=√6cm…①
図

△BAIは直角三角形の辺の比より、
AI:IB=1:√3
AI:√6=1:√3
AI=√2cm
△IBCは直角二等辺三角形なので、
IB=CI=√6cm
AC=AI+CI=（√2+√6）cm…②
①、②より、△ABCの面積は、
(√2+√6)×√6×1/２
=3+√3 cm²
図