2025年度宮城学力検査問題過去問【数学】

■問題PDF　

■目次　

■大問１

１-１：第一問次の1~8の問いに答えなさい。

5−(−4) を計算しなさい。

解答 ： 9

解説 ： 5-(-4)=5+4=9

１-２：6÷(−2/7 ) を計算しなさい。

解答 ： -21

解説 ： 6÷(−2/7 )=6×(-7/2)=3×-7=-21

１-３：(−2a)²×5b を計算しなさい。

解答 ： 20a²b

解説 ： (−2a)²×5b=4a²×5b=20a²b

１-４：等式 a+7b−3=0 をbについて解きなさい。

解答 ： b=-1/7a+3/7

解説 ：
a+7b−3=0
7b=-a+3
b=[-a+3]/7
b=-1/7a+3/7

１-５：15/√3+√27を計算しなさい。

解答 ： 8√3

解説 ： 15/√3+√27=15√3/3+3√3=5√3+3√3=8√3

１-６：yはxの2乗に比例し、x=6 のときy=−9 です。このとき、yをxの式で表しなさい。

解答 ： y=-1/4x²

解説 ： yがxの2乗に比例するということで、y=ax²の式になります。この式に、x=6,y=-9を代入します。
-9=(6)²a
-9=36a
a=-9/36
a=-1/4
a=-1/4をy=ax²に代入します。
y=-1/4x²

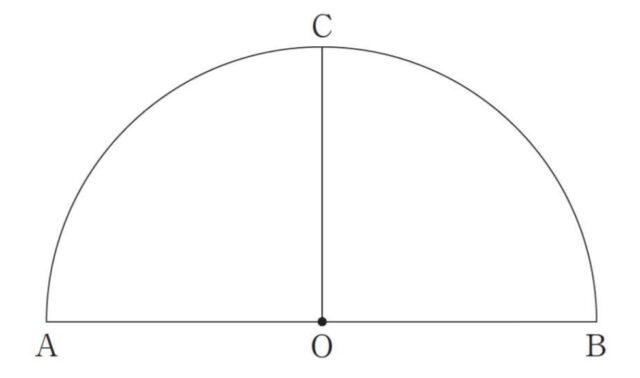
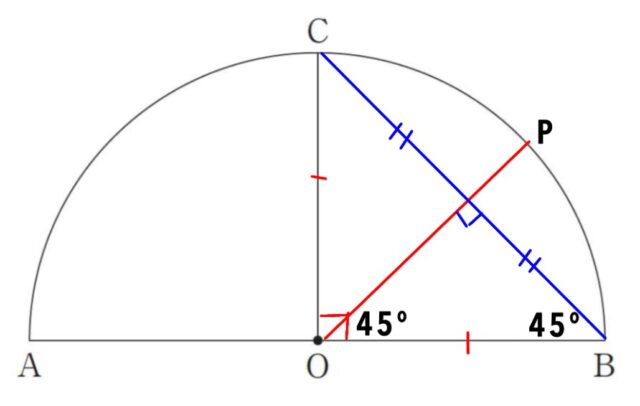
１-７：下の図のような、線分ABを直径とする半円があり、線分ABの中点をOとします。点Oを通って線分ABに垂直な直線と弧ABとの交点をCとします。弧BC上にあって、∠POB=45°となる点Pを作図によって求めるとき、その作図の方法を説明したものとして、誤っているものを、あとのア〜エから1つ選び、記号で答えなさい。
図

ア ∠COB の二等分線と弧BC との交点をPとする。
イ 点Aと点Cを結び、∠CAB の二等分線と弧BC との交点をPとする。
ウ 点Bと点Cを結び、線分BCの垂直二等分線と弧BC との交点をPとする。
エ線分OCの垂直二等分線と弧BC との交点をPとする。

解答 ： エ

解説 ：
ア：線分ABの中点Oは円の中心です。AB⊥COだから、∠COBを二等分すれば∠POB＝45°となります。
よって、Ｐは弧ＢＣの中点です。

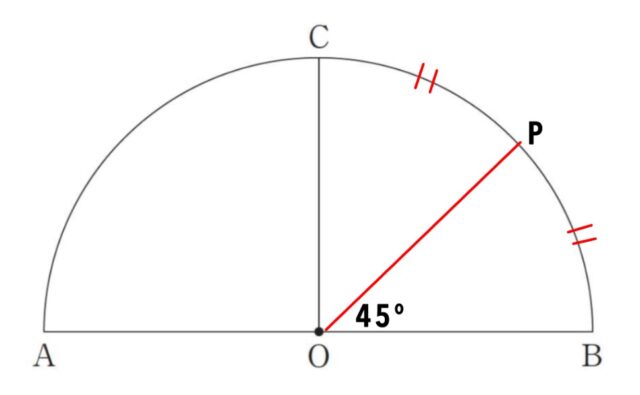
イ：長さの等しい弧に対する円周角の大きさは等しいです。逆に、円周角が等しければ弧も等しいです。
よって、Pは弧BCの中点で、∠POB＝45°になります。

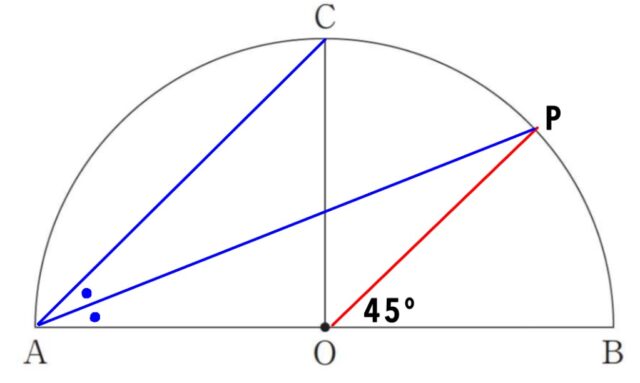
ウ：△COBは直角二等辺なので、∠CBO＝45°
線分BCの垂直二等分線はＯを通り、２つの直角二等辺に分割します。よって、∠POB＝45°になります。

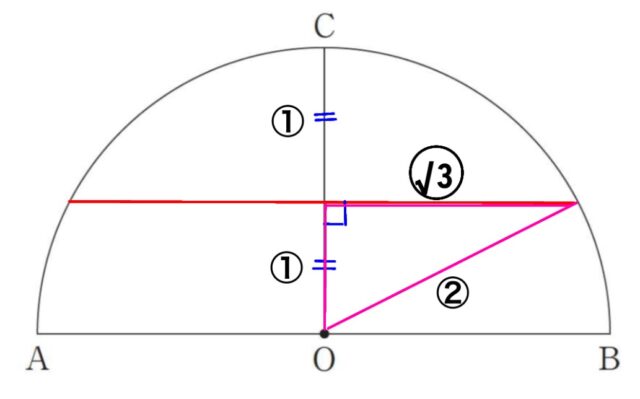
エ：線分OCの垂直二等分線をひくと、桃色の三角形は辺の比が1:2:√3となります。
直角二等辺ではないため、∠POB≠45°ではないので誤りです。

１-８：ある学年で、クロールで25mを泳いだときの記録をとりました。下の表は、このときの、A組の生徒25人とB組の生徒30人の記録を、累積度数をふくめて度数分布表に整理したものです。 A組とB組を比べたとき、18.0秒以上20.0秒未満の階級の累積相対度数が大きい組と、その累積相対度数を答えなさい。
表

解答 ： [18.0秒以上20.0秒未満の階級の累積相対度数が大きい組は]A[組で、その累積相対度数は]0.64[である。]

解説 ： 累積相対度数は、その階級までの累積度数を合計の度数で割った値です。
累積相対度数= 累積度数/合計度数
・A組の累積相対度数
この階級の累積度数: 16 (人)
合計度数: 25 (人)
A組の累積相対度数=16/25=0.64
・B組の累積相対度数
この階級の累積度数: 18 (人)
合計度数: 30 (人)
B組の累積相対度数=18/30=3/5=0.60

0.64>0.60 なので、累積相対度数が大きい組はA組です。

■大問２

２-１（１）：第二問次の1~4の問いに答えなさい。
1 下の図は、Pに整数を入れると、①~④の順に計算が行われ、Qの値が導き出される過程を表しています。アには①、イには②、ウには③の計算を行った結果の値がそれぞれ入ります。 あとの(1)、(2)の問いに答えなさい。
図

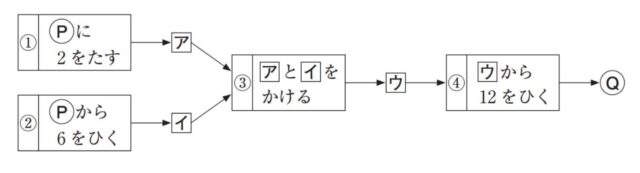
(1) P に入れる整数を1とするとき、Q の値を求めなさい。

解答 ： -27

解説 ： 問題の手順にしたがって解きます。
①1+2=3…ア
②1-6=-5…イ
③3×-5=-15…ウ
④-15-12=-27…Q

２-１（２）：Pにある整数を入れると、Qの値がPに入れた整数と同じ値になりました。
Pに入れた 整数をxとするとき、xをすべて求めなさい。

解答 ： -3,8

解説 ： p=xとすると、
①x+2…ア
②x-6…イ
③(x+2)(x-6)…ウ
④(x+2)(x-6)-12…Q
Q=Pなので、
(x+2)(x-6)-12=x
x²+(2−6)x+2×(−6)−12=x
x²−4x−12−12=x
x²−4x−24=x
x²−4x−x−24=0
x²−5x−24=0
(x−8)(x+3)=0
x=8,-3

２-２（１）：下の図のように、比例y=3/2xのグラフ上と反比例y=a/xのグラフ上に、x 座標が4である点A,点B をそれぞれとり、点Aと点Bを結びます。また、比例y=3/2x のグラフ上に、点Bとy 座標が 等しい点Cをとり、点Bと点Cを結びます。ただし、a<0 とします。
次の(1)、(2)の問いに答えなさい。
図

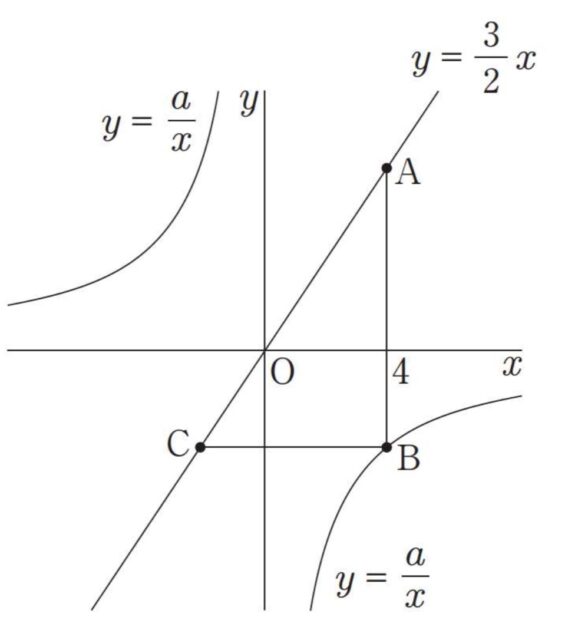
(1) 点Aのy 座標を求めなさい。

解答 ： 6

解説 ： 点 A は、比例 y=3/2のグラフ上にあり、そのx座標は4です。
y=3/2xに x=4 を代入すると、
y=3/2×4
y=3×2
y=6

２-２（２）：線分ABとx軸との交点をDとします。AD=BCとなるとき、a の値を求めなさい。

解答 ： -12

解説 ： 点 A: x 座標は 4 で、 y=3/2x 上にあるため、(1)より A(4,6) です。
点 B: x 座標は 4 で、y=a/x上にあるため、 y=a/4です。 B(4,a/4)
点 C: y 座標は点 B と等しく a/4で、y=3/2x 上にあるため、a/4=3/2x⟹x=a/4×2/3=2a/12=a/6 C(a/6,a/4)
線分 AB は x 座標が 4 で一定なので、 x 軸に垂直な直線です。したがって、x 軸との交点 D の座標は y 座標が 0 の点であり、D(4,0) AD=BCより、
点 A(4,6) と点 D(4,0) は x 座標が等しいので、長さは y 座標の差の絶対値です。
AD=∣6−0∣=6
点 B(4,a/4) と点 C(a/6,a/4) は y 座標が等しいので、長さは x 座標の差の絶対値です。
BC= | 4− a/6 |
6=| 4−a/6 |
【4−a/6=6 の場合】
−a/6=6−4
−a/6=2
a=2×(−6)
a=−12
【4−a/6=−6の場合】
−a/6=−6−4
−a/6=−10
a=−10×(−6)
a=60
a<0 より、a=−12 です。

２-３（１）：図Ⅰのような、∠ABC=∠ABD=∠DBC=90°である三角錐ABCDがあります。辺AB上に、 点E をAE:EB=3:1 となるようにとります。また、辺AC、辺AD 上に、それぞれ点F、点Gを面BCDと面EFGが平行となるようにとります。

次の(1)、(2)の問いに答えなさい。
(1) 三角錐ABCDと三角錐AEFGの体積の比を求めなさい。
図Ⅰ

解答 ： [（三角錐ABCD）：（三角錐AEFG）] 64:27

解説 ： 相似な立体における対応する辺の比は、相似比に等しくなります。
辺 AB と辺 AE は対応する辺です。
問題文より、辺 AB 上の点 E が AE:EB=3:1 とあります。
したがって、
AE=3k,EB=1kとすると、
AB=AE+EB=3k+1k=4k
三角錐 AEFG と三角錐 ABCD の対応する辺の比は、AE:AB です。
AE:AB=3k:4k=3:4
よって、2つの三角錐の相似比は 3:4 です。
相似な立体の体積の比は、相似比の3乗に等しくなります。
(体積比)=(相似比)³
三角錐AEFGの体積:三角錐ABCDの体積=(AE:AB)³
三角錐AEFG:三角錐ABCD=3³:4³
三角錐AEFG:三角錐ABCD=27:64

２-３（２）：図Ⅱは、図I において、点Bと点F、点Bと点Gをそれぞれ結んだものです。
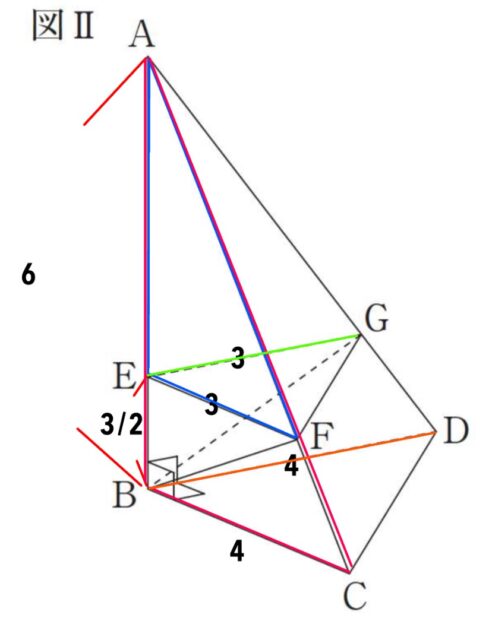
AB=6 cm、 BC=BD=4 cm のとき、三角錐BEFGの体積を求めなさい。
図Ⅱ

解答 ： 9/4[cm³]

解説 ： △ABC∽△AEFより、EF＝3cmとなります。
同様に△ABD∽△AEGで、EG=3cmです。
問題文より、辺 AB 上の点 E が AE:EB=3:1 とあります。
EB=6×①/④＝3/2cm
三角錐B-EFGの体積は、3×3÷2×3/2=9/4cm³
図

２-４（１）：下の図のような、円盤、マス目、コマがあります。円盤には、1から4までの数字が書いてあります。この円盤はまわすことができ、円盤とは別に針が固定されています。まわした円盤が静止すると、針が指す場所に書いてある数字が、必ず1つ決まります。マス目には、スタートの文字と、A からH までのアルファベットが書いてあり、C、 E、 F のマスには指示が書いてあります。
図

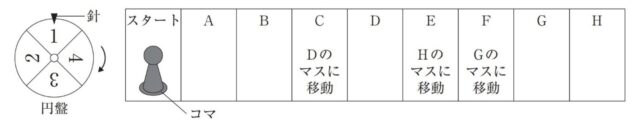
円盤を1回まわすごとに、次の「」にしたがってコマを移動させます。
「・円盤をまわして決まった数字と同じ数のマスだけ、コマがあるマスからH のマスの方向に 向かって、コマを移動させる。
・コマを移動させてC、 E、 F のマスに止まったときは、それぞれそのマスに書いてある指示 にしたがってコマを移動させる。」
たとえば、コマをスタートのマスに置き、円盤を1回まわして決まった数字が2のとき、B のマスにコマを移動させます。
次の(1)、(2)の問いに答えなさい。ただし、円盤をまわして決まる数字は、1から4までのどの 数字に決まることも同様に確からしいものとします。


(1) コマをスタートのマスに置き、円盤を1回まわします。このとき、コマがD のマスにある確率 を求めなさい。

解答 ： 1/2

解説 ： コマをスタートのマスに置き、円盤を1回まわします。円盤をまわして出る数字は 1,2,3,4 のいずれかで、これらは同様に確からしいため、それぞれの数字が出る確率は、1/4です。
コマが D のマスに最終的に到着するのは、円盤をまわして決まった数字が3また4 の場合の2通りです。

数字が 3 の場合: スタート→C に止まり、指示により D へ移動。
数字が 4 の場合: スタート→D に止まる。

(D)=P(数字3)+P(数字4)=1/4+1/4=2/4=1/2

２-４（２）：コマをスタートのマスに置き、円盤を2回まわします。このとき、コマがH のマスにある確率 を求めなさい。

解答 ： 3/8

解説 ： まず、円盤を2回まわすので、出る目の組み合わせは全部で 4×4=16 通りです。
この16通りのうち、最終的にコマがHに着くのが何通りあるかを数えれば、確率が分かります。
1回目と2回目に出る目を (1回目の目, 2回目の目) のように表し、コマの動きを追いかけましょう。
・1回目が「1」のとき (コマはAにいる)
Aから4マス進むとEに着き、指示でHへ移動します。→ 目の組み合わせは (1, 4)
・1回目が「2」のとき (コマはBにいる)
Bから3マス進むとEに着き、指示でHへ移動します。→ 目の組み合わせは (2, 3)
・1回目が「3」のとき (コマはC→Dにいる)
Dから1マス進むとEに着き、指示でHへ移動します。
Dから4マス進むと、そのままHに着きます。
→ 目の組み合わせは (3, 1) と (3, 4)
・1回目が「4」のとき (コマはDにいる)
1回目が「3」のときと同じく、Dからスタートします。→ 目の組み合わせは (4, 1) と (4, 4)

まとめると、Hに着く目の組み合わせは、(1, 4), (2, 3), (3, 1), (3, 4), (4, 1), (4, 4)
の6通りです。
全部で16通りのうち、Hに着くのは6通りなので、確率は次のようになります。
6/16=3/8

■大問３

３-１（１）：第三問　花さんと大地さんは、図Ⅰのような、 ボンベをセットして使用するカセットコンロの、 ガスの消費量やボンベに残るガスの量について 調べています。
次の1、2の問いに答えなさい。
図Ⅰ

1 花さんは、カセットコンロのガスの消費量をウェブサイトで調べました。下の表は、カセットコンロの用途と、それぞれの用途で1回使用したときのガスの消費量についてまとめたものです。この表をもとにしてガスの消費量を考えるとき、あとの(1)、(2)の問いに答えなさい。
表

(1) 表の①の用途でa 回、②の用途でb 回使用するとき、ガスの消費量の合計をa とb を使った 式で表しなさい。

解答 ： 50a+15b[g]

解説 ： ガスの消費量の合計は、「①の用途での消費量」と「②の用途での消費量」を足したものです。
表より、「①の用途での消費量」は50ag、「②の用途での消費量」は15bgとわかるので合計消費量は、
合計消費量=50a+15b (g)

３-１（２）：(2) 花さんの自宅には、ガスが240 g 入ったボンベが6本あります。②の用途で使用する回数が①の用途で使用する回数の2倍となるようにして、このボンペ6本分のガスをすべて消費するとき、①の用途で使用できる回数は何回になりますか。

解答 ： 18[回]

解説 ： 問題文よりボンベ1本あたりのガスが240 g、ボンベの本数が6 本なので、
ガスの総量は、240×6=1440 g　となります。
⑴で、50a+15bなので、
50a+15b=1440
② の回数 (b) は ① の回数 (a) の2倍なので、
b=2a
これを50a+15b=1440の式に代入します。
50a+15(2a)=1440
50a+30a=1440
80a=1440
a=1440/80
a=18

３-２（１）：花さんと大地さんは、図Ⅰと同じカセットコンロ A、 B を準備しました。
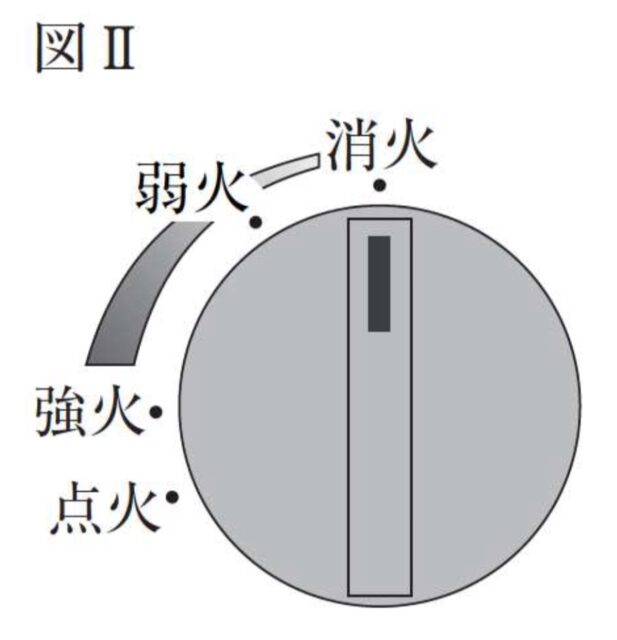
これらのカセットコンロは、図Ⅱのようなつまみをまわして火の強さを調節できます。ボンベのガスの量が240 g のとき、「強火」の設定では 60分間、「弱火」の設定では180分間使用すると、それぞれボンベのガスがすべてなくなります。
次の(1)、(2)の問いに答えなさい。ただし、火の強さを固定して使用するとき、火の強さに応じてガスは一定の割合で消費されるものとします。 また、つまみをまわしているときの時間とガスの消費量は考えないものとします。
図Ⅱ

(1) ガスが240 g 入ったボンベをセットして、カセットコンロを「強火」の設定で20分間使用 したあとに、ボンベに残るガスの量は何gですか。

解答 ： 160[g]

解説 ： 「強火」の設定では、240 g のガスを 60 分間で全て消費するので、強火で一分間に消費するガスの量は240/60=4g/分
これを20分消費するので、
20×4=80g消費します。
よって、残ったガス量は、
240-80=160g

３-２（２）ア：花さんと大地さんは、カセットコンロを使用したときにポンベに残るガスの量を調べようと 思いました。はじめに、2人はカセットコンロA、 B にガスが240 g 入ったボンベをそれぞれセットして同時に点火しました。次の「」は、2人が点火したあと火の強さをそれぞれ設定 し、カセットコンロを使用したようすを示したものです。
「・花さんは、カセットコンロA を、「弱火」と「強火」の間に設定した。途中で火の強さを変え ずに使用し、点火してからちょうど80分後にボンベのガスがすべてなくなった。
・大地さんは、カセットコンロB を、はじめに 「強火」の設定で40分間、そのあと、「弱火」 の設定に変えて使用した。使用し続けるとボンベのガスがすべてなくなった。」
花さんと大地さんは、カセットコンロを使用したようすについて話し合いました。下の【　】は、花さんと大地さんの会話です。
あとの(ア)、(イ)の問いに答えなさい。

【花さん: カセットコンロA について、点火してからボンベのガスがすべてなくなるまでの グラフをかいてみるね。カセットコンロを点火してからx 分後の、ボンベに残る ガスの量をy g とすると、
x とy との関係を表すグラフは図Ⅲのようになるね。
大地さん:私もカセットコンロB について、花さんと同じようにグラフをかいてみよう。 私のかいたグラフを図Ⅲにかき写してみると何かわかることはあるかな。
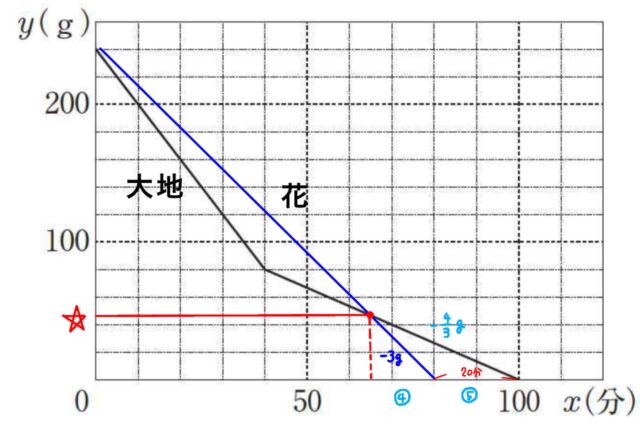
花さん: 点火してから80分後までの間に、点火したときとは別に、それぞれのボンベに残るガスの量が等しくなるときがあるね。
大地さん: ボンベに残るガスの量が等しくなるときのガスの量を表しているのは、2つのグラフのa の値だね。計算して求めてみよう。】


(ア) カセットコンロB について、点火 してからボンベのガスがすべてなくなるまでの、x とy との関係を表す グラフを、解答用紙の図にかき入れなさい。

解答 ：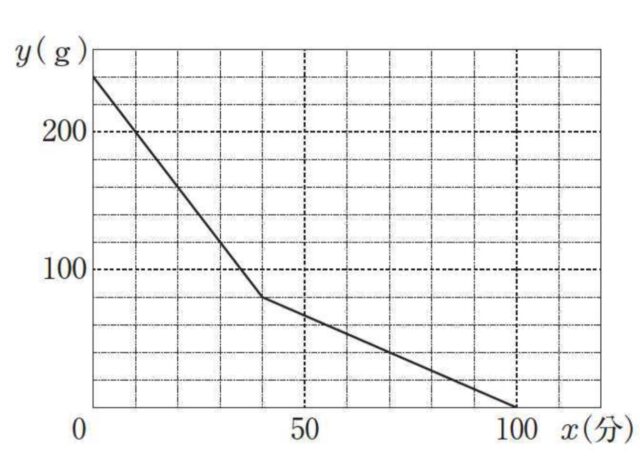

解説 ： 弱火の消費速度は4/3g/分（180 分間で 240 g を消費）
ガスがすべてなくなる時間は
80÷4/3=80×3/4=60分 です。

３-２（２）イ：(イ) 会話のa にあてはまる適切な言葉を書きなさい。また、点火したときとは別に、 カセットコンロA、 B のそれぞれのボンペに残るガスの量が等しくなるときの、ボンベに残るガスの量を求めなさい。

解答 ： a（例）交点のy座標　48[g]

解説 ： a：花さんと大地さんの会話は、2つのグラフが交わる点について話しています。グラフの交点は、「x 軸（時間）」と「y 軸（ガスの量）」の両方が等しくなる点です。
「ボンベに残るガスの量が等しくなる」という「ガスの量」を表しているのは、グラフの縦の軸（y 軸）の値です。

２つのボンベに残るガスの量が等しくなるときのガスの量は２つのグラフの交点のｙ座標です。
大地は60分で80ｇなので、傾きは－80/60＝－4/3
花子は格子点に着目すると20分で60ｇなので、傾きは－60/20＝－3
グラフの交点から右側に注目します。ガスの減少割合を速さで捉えると、
ガスの減少速度の比は、花：大地＝３：４/３＝９：４
ガスの残量が等しい交点からガスがなくなるまでの時間は逆比で、花：大地＝④：⑨
差の⑤が20分にあたるから、④＝16分です。
したがって、交点のｙ座標は、３×16＝48ｇ

■大問４

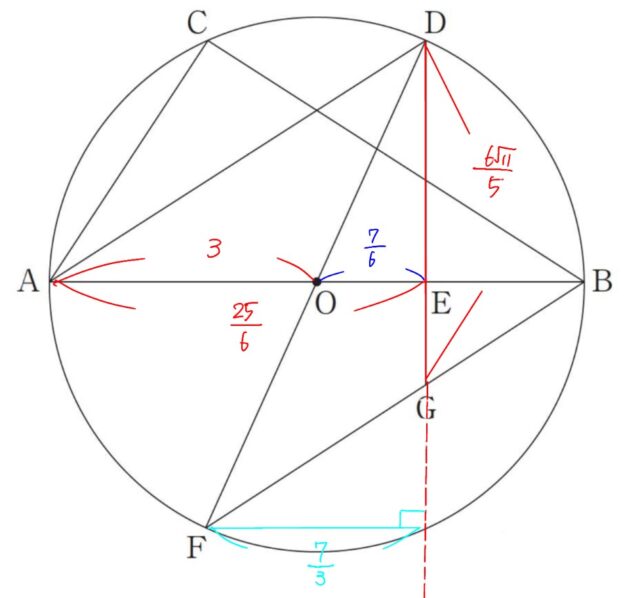
４-１：第四問　長さが6 cm の線分ABを直径とする円O があります。図Ⅰのように、円O の周上に、点CをBC=5 cm となるようにとり、点Aと点C、点Bと点Cをそれぞれ結びます。また、点Aをふくま ない方の弧BC上に、点Dを弧AC=弧BD となるようにとり、点Aと点Dを結びます。さらに、点D から 線分ABに垂線をひき、線分ABとの交点をEとします。
次の1~4の問いに答えなさい。
1 線分ACの長さを求めなさい。
図Ⅰ

解答 ： √11

解説 ： 直径 AB に対する円周角は 90°なので、△ABC は ∠ACB=90°の直角三角形になります。

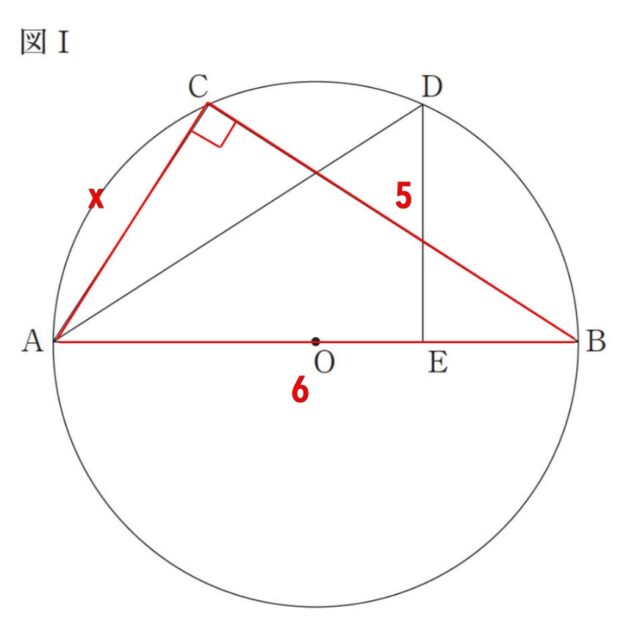
直角三角形 ABC において、三平方の定理を使って、線分 AC の長さを求めます。

x²+5²=6²
x²+25=36
x²=36−25
x²=11
x>0 なので、
x=√11

４-２：△ABC∽△DAE であることを証明しなさい。

解答 ： （例）△ABCと△DAEにおいて
線分ABは円Oの直径だから
∠BCA=90°…①
仮定から∠AED=90°…②
①、②より
∠BCA=∠AED…③
仮定から弧AC=弧BD
1つの円において、等しい弧に対する円周角は等しいから
∠ABC=∠DAE…④
③、④より、2組の角がそれぞれ等しいから
△ABC∽△DAE

解説 ： ※解答の証明と被る内容になりますが、少しだけ詳しく解説していきます。
AB は円 O の直径であるので、直径に対する円周角は 90°です。
∠BCA=90°⋯①
点 D から線分 AB に垂線 DE を引いたので、
∠AED=90°⋯②
①, ② より、
∠BCA=∠AED(=90°)⋯③
問題の条件より、弧AC=弧BD です。
等しい弧に対する円周角は等しいので、弧 AC に対する円周角 ∠ABC と、弧 BD に対する円周角 ∠DAB は等しくなります。
∠ABC=∠DAB
∠DAB は、△DAE の ∠DAE と同じ角です。
∠DAB=∠DAE
したがって、
∠ABC=∠DAE⋯④
③, ④ より、2組の角がそれぞれ等しいので、△ABC と △DAE は相似です。

４-３：線分AEの長さを求めなさい。

解答 ： 25/6[cm]

解説 ： はじめに、線分 DA の長さを求めます。
弧AC=弧BD であるため、等しい弧に対する弦の長さも等しいです。
BD=AC
△ABC は直径 AB を斜辺とする直角三角形なので、三平方の定理より
AC= √[AB²−BC²]= √[6²−5²]= √[36−25] =√11cm
よって、BD=√11cm
AB は直径なので、△DAB も ∠ADB=90°の直角三角形です。三平方の定理より
DA²+BD²=AB²
DA²+(√11)²=6²
DA²+11=36
DA²=25
DA=5 cm
△ABC∼△DAE より、対応する辺の比は等しいので、
相似比は AB:DA=6:5 です。
BC:AE=AB:DA
5:AE=6:5内項の積と外項の積は等しいので
6×AE=5×5
6×AE=25
AE=25/6 cm

４-４：図Ⅱは、図I において、直線DOと円O との交点のうち、D 以外の点をF とし、点Bと点Fを結んだものです。また、線分DE をE の方に延長した直線と線分BFとの交点をG とします。
△DFG の面積を求めなさい。
図Ⅱ

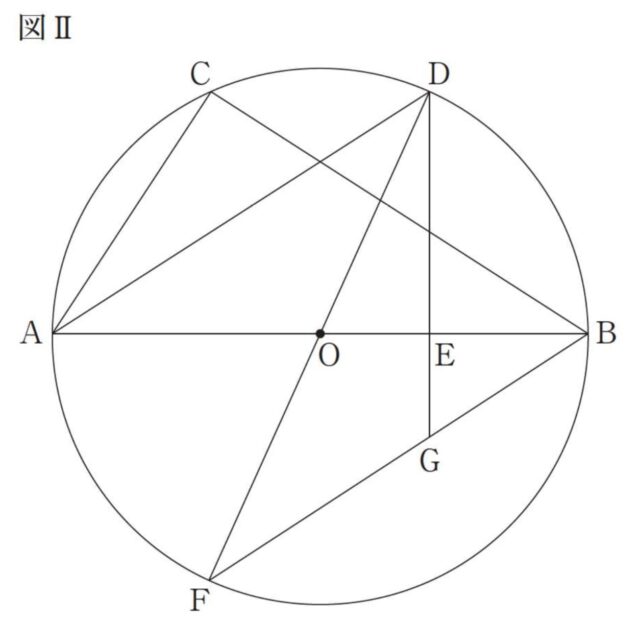
解答 ： 7√11 /5 [cm²]

解説 ：
既知の長さ:
直径 AB=6
半径 OA=OB=3
BC=5
AC=√11
AC=BD より BD=√11です。
AE=25/6
△DEB で三平方の定理、または相似比から DE の長さを計算します。
DE= √[BD²−EB²= 5√11/6

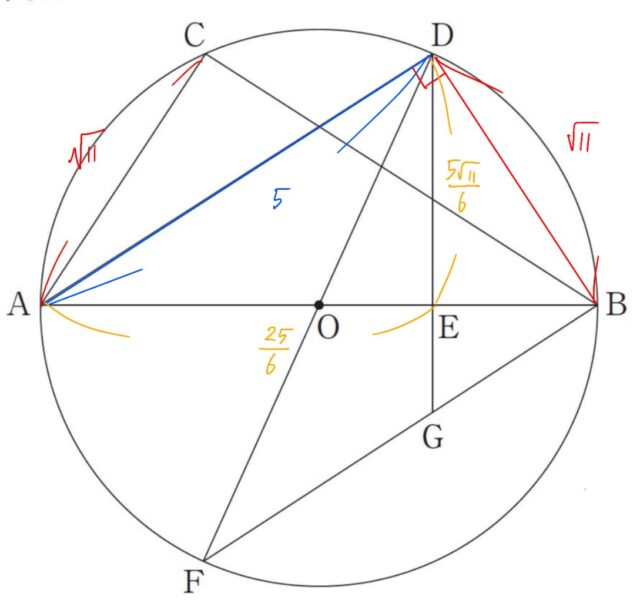
1.面積の高さを求めます。
△DFG の面積を、DG を底辺とし、F から DG に引いた垂線の長さを高さとして求めます。
DG は線分 AB に垂直な直線上にあります。D と F は円の中心 O に対して点対称な位置にあるため、F から DG までの距離（高さ h）は、O から DG までの距離のちょうど2倍になります。
O から DG までの距離は OE の長さなので、
OE=OB−EB=3− 11/6= 7/6
高さ h:h=2×OE=2× 7/6= 7/3

2.底辺 DG の特定します。
DG=DE+EG です。EG の長さを求めるために、相似な三角形を利用します。
補助線: F から AB に垂線 FH を引きます。D と F が O の点対称なので、DE=FH、OE=OH となります。
FH=DE=5√11/6
​相似: DE∥FH より、△GBE と △GFH は相似です。
相似比 BE:BH:BE/BH= 11/6 /25/6=11/25
EG の長さ: 相似比 GE:GH=11:25 を利用します。
GE/FH= EB/HB⟹GE=11/25×FH
GE=11/25× 5√11/6= 11√11/30
底辺 DG=DE+GE= 5√11/6+11√11/30
DG= 25√11/30+ 11√11/30= 36√11/30=6√11/5

3面積を計算します。
面積 S= 1/2×底辺 DG×高さ h
S=1/2× 6√11/5×7/3
S=42√11/30=7√11/5