■問題PDF
令和7年度_学力検査問題過去問【奈良】- 数学
令和7年度_学力検査問題過去問【奈良】- 数学 解答
■目次
大問1
大問2
大問3
大問4
■大問1
次の各問いに答えよ。
次の①~④を計算せよ。
1-1①:2+(-7)
解答 : -5
解説 : 2+(-7)=2-7=-5
1-1②:-5²÷4
解答 : -25/4
解説 : -5²÷4=-25/4
1-1③:3a²b÷6b×2a
解答 : a³
解説 : 3a²b÷6b×2a=1a²/2×2a=a³
1-1④:(x²+1)-(x-2)²
解答 : 4x-3
解説 : (x²+1)-(x-2)²=(x²+1)-(x²-4x+4)=x²+1-x²+4x-4=4x-3
1-2:連立方程式 6x-y=13 2x+3y=1を解け。
解答 : x=2,y=-1
解説 : 6x-y=13…①
2x+3y=1…②
①×3より、
3(6x-y)=13×3
18x-3y=39…①’
①’と②を加減法で解きます。
x=2,y=-1
1-3:2.5<√a<4 を満たす自然数aは何個あるか。
解答 : 9個
解説 : この不等式の各辺を2乗します。不等式の各辺が正の数であるため、大小関係は変わりません。
(2.5)² = 6.25
(√a)²= a
(4)² = 16
したがって、aの満たすべき条件は、6.25 < a < 16
aは自然数です。この範囲を満たす整数aの値は
a = 7, 8, 9, 10, 11, 12, 13, 14, 15 となります。
1-4:1足x円の定価で販売している靴を、7月には定価の30%引きで販売し、8月には7月の販売価格の10%引きで販売した。8月の靴1足の販売価格を文字式で表せ。
解答 : 63/100 x円
解説 : 7月の販売価格は、定価の30%引きで販売したのでx×(1- 3/100) =7/100 x円 8月の販売価格は 7月の販売価格の10%引きで販売したので、(0.7x)×(1- 1/100) =[7/100 x] x [9/100]=63/100 x円
1-5: 図1のように、-1, 0, 1, 2, 3の数を書いたカードがそれぞれ1枚ずつある。この5枚のカードをよくきってから、2枚同時にカードをひく。このとき、ひいた2枚のカードに書かれた数の積が自然数である確率を求めよ。
解答 : 3/10
解説 : 5枚のカードから2枚を同時にひく組み合わせの総数を求めます。
(-1, 0), (-1, 1), (-1, 2), (-1, 3)(0, 1), (0, 2), (0, 3)(1, 2), (1, 3)(2, 3)全ての場合の数は10通りです。
積が正になるのは、「両方とも正の数」または「両方とも負の数」の場合です。
この条件にあうのは、(1, 2)(1, 3) (2, 3)の3通りのみです。
よって、求める確率は3/10です。
1-6:図2で、∠xの大きさを求めよ。
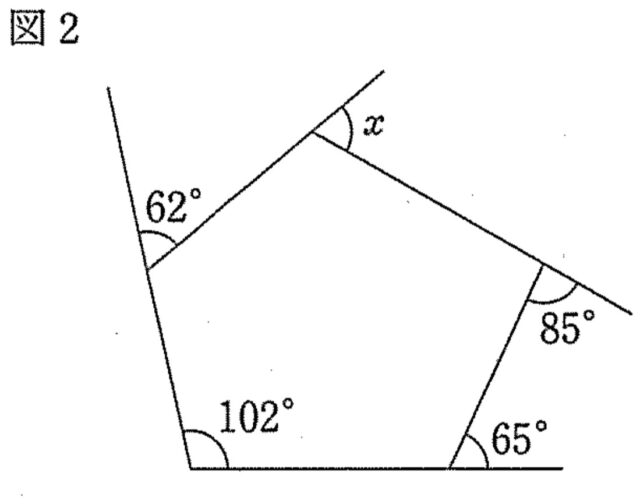
解答 : 70度
解説 : 図に示されている五角形の内角を求めていきます。
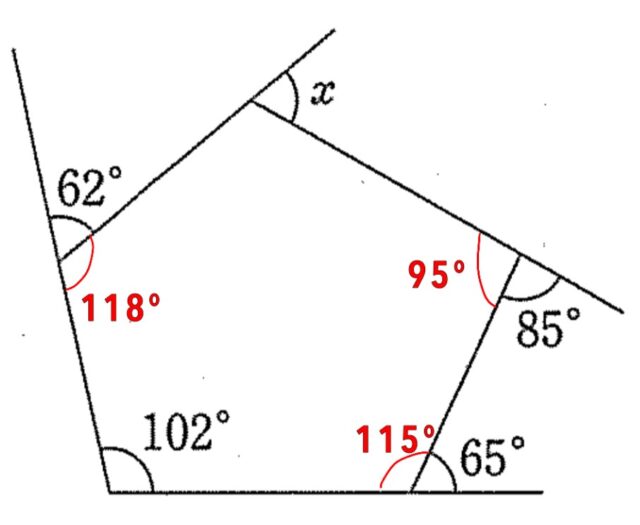
五角形の内角の和は540°です。
∠xに接している五角形の内角は
540-(118+102+115+95)=540-430=110°です。
∠x+接する五角形の内角=180°となるので、
∠x=180-110=70°
1-7:図3で、△A’B’C’は、△ABCを回転移動したものである。回転の中心である点Oを、定規とコンパスを使って解答欄の枠内に作図せよ。なお、作図に使った線は消さずに残しておくこと。

解答 : 
解説 : 対応する点を結んだ線分を2組選び、それぞれの垂直二等分線を作図します。
・線分BB’の垂直二等分線を作図します。
・線分CC’の垂直二等分線を作図します。
交点Oの特定手順1で引いた2本の垂直二等分線が交わる点が、求める回転の中心Oです。
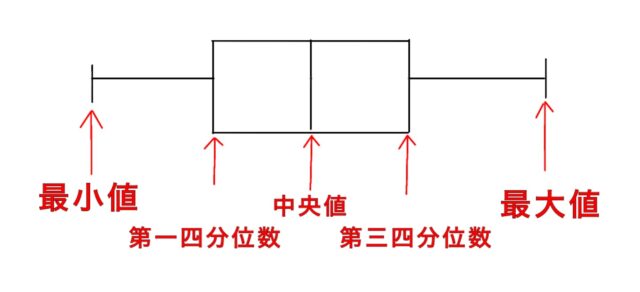
1-8:図4は、15個のみかんの1個ごとの重さのデータをヒストグラムに表したものである。例えば、80g以上85g未満の重さのみかんは1個である。このデータを箱ひげ図に表したものとして適切なものを、図5のア~オから1つ選び、その記号を書け。
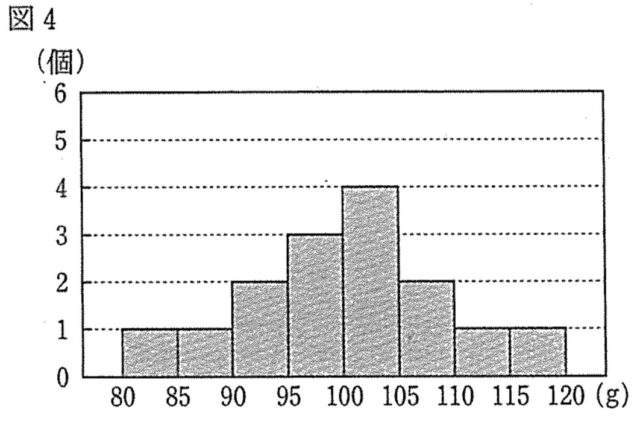

解答 : エ
解説 : 図4より、下記のことが分かります。
中央値:前から8番目の値です。(100g~105gの階級)
第一四分位数:前から4番目の値です。(90g~95gの階級)
第三四分位数:前から12番目の値です。(105g~110gの階級)
これをもとに適する箱ひげ図を選びます。
■大問2
花子さんと太郎さんは、3年生を送る会での3年生への贈り物について考えているとき、お菓子のパッケージには三角すいの形のものがあることに興味をもった。各問いに答えよ。

次の[ ]内は、三角すいの形のパッケージについて考えている、花子さんと太郎さんの会話である。①、②の問いに答えよ。
[花子: 3年生への贈り物として、三角すいの形をしたパッケージに記念品を入れてプレゼントをしようよ。
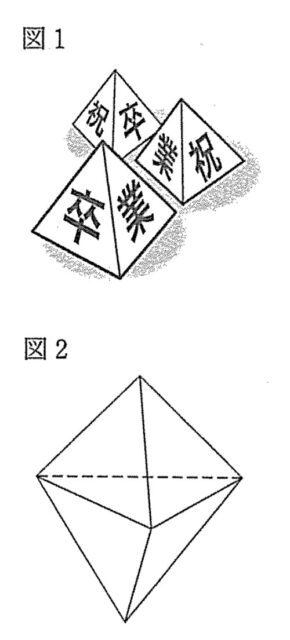
太郎: 展開図がかきやすい正四面体で考えてみたよ。正四面体の3つの面にそれぞれ1つずつ文字を書いて、「祝卒業」の文字を入れたらどうかな。図1のように文字が見える正四面体になるように展開図をかいてみたよ。
花子: 展開図をもとに作った正四面体2つを面がぴったり重なるようにくっつけると、図2のような、全ての面が合同な正三角形でできた立体ができたよ。
太郎: 面が6つだから、この立体は正六面体といえるのかな。
花子: 正多面体の特徴から考えると、この立体は正多面体ではないので、正六面体とはいえないよ。]
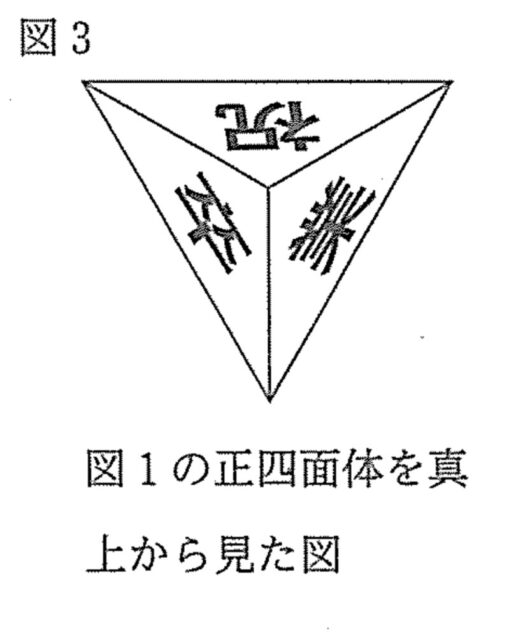
2-1①:次のア~エの展開図の中に、組み立てると図3の正四面体ができるものがある。その展開図をア~エから全て選び、その記号を書け。
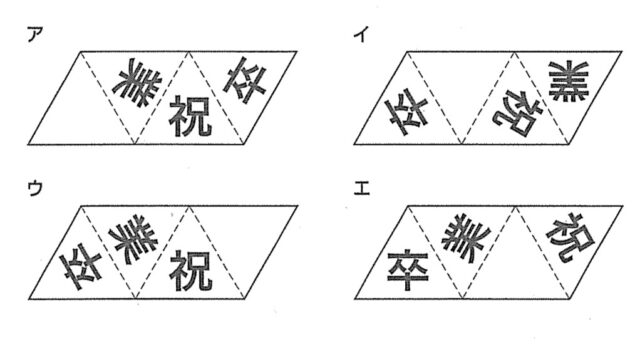
解答 : イ,エ
解説 : ア: 組み立てると、「祝」と「業」の面が底面に接する辺を共有しますが、図3のように文字の向きが頂点に向かって集まっていません。
イ:「卒」「業」「祝」の文字がすべて立体の頂点側を向くように配置されています。また、組み立てて真上から見ると、図3と同じく「祝」「卒」「業」が時計回りの配置になります。
ウ:「卒」「業」「祝」の文字がすべて立体の頂点側を向くように配置されています。また、組み立てて真上から見ると、図3と同じく「祝」「卒」「業」が時計回りの配置になります。
エ: 組み立てると、「卒」と「祝」の面が底面に接する辺を共有しますが、図3のように文字の向きが頂点に向かって集まっていません。
2-1②:下線部のようにいえる理由を、「1つの頂点」と「面」の語句を用いて簡潔に書け。
解答 : (例)1つの頂点に集まる面の数が、全て同じではないから。
解説 : 正多面体であるためには、以下の2つの条件を満たす必要があります。 ・全ての面が合同な正多角形である。 ・どの頂点においても、集まる面の数が等しい。 しかし、この立体には頂点が5つあり、集まる面の数が等しくありません。したがって、下線部の理由として、「1つの頂点に集まる面の数が、全て等しくないから」と述べることができます。
花子さんと太郎さんは、三角すいの形をしたお菓子のパッケージを開けると平たい袋になったことに興味をもち調べたところ、図4のように筒状の紙から三角すいを作る【作り方】を見つけた。【作り方】のとおりに作ってできた三角すいの各辺の長さを調べ、図5のように AB=BC=CD=AD, AC=BDとなる三角すいABCDをかいた。次の[ ]内は、図5をみて考えた、花子さんと太郎さんの会話であるAB=√3cm, AC=2cmとして、①、②の問いに答えよ。
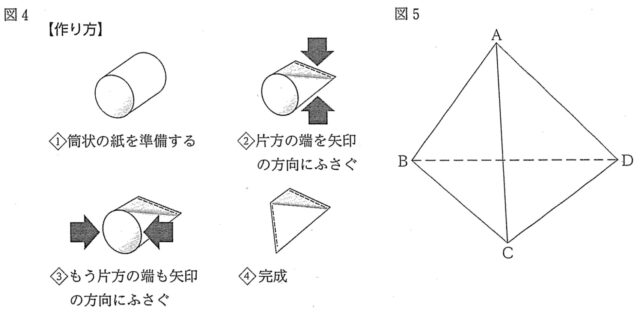
[花子: 調べてみると、このパッケージの長所は、内側に空間が保持できるため中身を保護できることや、デザイン性が高いことのようだよ。
太郎: 作りやすいというよさもあるね。図5の三角すいABCDは、同じ長さの辺がたくさんあるね。三角すいABCDについて他にも特徴がないか調べてみよう。
花子: 図5の三角すいABCDに、図6のように辺ACの中点MをとるとBM=DM=あcmだね。
太郎:△MBDの3辺の長さから、∠BMD=い°なので、面ABCと面ACDの位置関係もわかるね。]
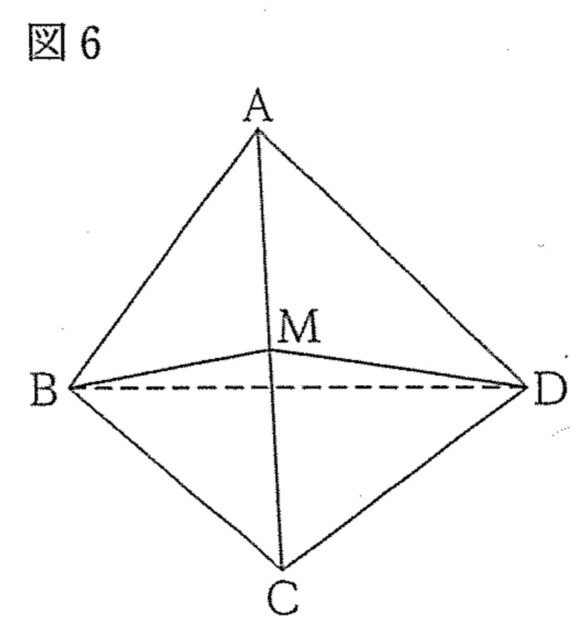
2-2①:あ、いに当てはまる数を、それぞれ書け。
解答 : あ:√2
い:90
解説 : あ:△ABCの辺の長さは、AB=√3、BC=√3、AC=2です。AB=BCなので、△ABCは二等辺三角形です。
Mは底辺ACの中点なので、BMはACに垂直に交わります。AMの長さはACの半分です。
AM=1/2AC=1/2×2=1cm
△ABMは直角三角形なので、三平方の定理の定理より、
[AM]²+[BM]²=[AB]²
1²+[BM]²=(√3)²
1+[BM]²=3
[BM]²=2
BM=√2cm
△ADCも同じAD=CD=√3の二等辺三角形なので、DMも同じ長さです。
い:いは△MBDの頂点Mの∠BMDです。
△MBDの3辺の長さは
BM=√2、DM=√2、BD=2です。
三平方の定理の逆が成り立つかを確認します。
[BM]²+[DM]²=(√2)²+(√2)²=2+2=4
[BD]²=2²=4
[BM]²+[DM]²=[BD]²
三平方の定理が成り立つので、△MBDはBDを斜辺とする直角三角形です。したがって、BDの向かいにある∠BMDは90°です。
2-2②:三角すいABCDの体積を求めよ。
解答 : 2/3 cm³
解説 : 三角すいABCDの体積を求めるために、面MBDで立体を2つに分けて考えます。△MBDの底面積=1/2×BM×DM=1/2×√2×√2=1/2×2=1cm²
・三角すいA-MBDの体積
1×1×1/3=1/3cm³
・三角すいC-MBDの体積
1×1×1/3=1/3cm³
よって求める体積は
1/3+1/3=2/3cm³
■大問3
右の図で、放物線は関数y=x²のグラフである。4点A, B, C, Dは放物線上の点であり、2点C, Dのx座標はそれぞれ2, 3である。直線AD、線分BCはx軸に平行である。点Pは放物線上を動く点であり、そのx座標は正の数である。点Qは点Pを通りy軸に平行な直線と直線ADとの交点である。原点をOとして、各問いに答えよ。

3-1:関数y=x²について、xの変域が-2≦x≦3のときのyの変域を求めよ。
解答 : 0≦y≦9
解説 : [最小値]変域-2≦x≦3の中にx=0が含まれているため、yはx=0で最小値をとります。最小値: y = 0²= 0
よって、x²のグラフは原点(0, 0)が最も低い点です。
[最大値]
y の最大値は、変域の端である x=−2 と x=3 のうち、原点からより遠い方の x 座標でとります。
∣−2∣=2
∣3∣=3
3>2 なので、 x=3 のとき y は最大値をとります。x=3の時のyは、y=3²=9
したがって、yの変域は0≦y≦9

3-2:2点B, Dを通る直線の式を求めよ。
解答 : y=x+6
解説 : はじめに2点BDの座標を求めます。
点Dの座標のx座標は3と与えられています。y座標はy=x²に代入して求めます。y=3²=9
よって、Dの座標は(3, 9)です。
直線BCはx軸に平行なので、点Cのy座標とBのy座標は同じです。点Cのx座標は2と与えられています。点Cのy座標はy= 2²=4
したがって、点Bのy座標は4です。y=x²にy=4を代入すると、4=x²からx=2です。図より、Bのx座標は負なので、x=-2です。Bの座標は(-2, 4)です。
傾きは、yの増加量/xの増加量=9-4 /3-(-2)=5/5=1
よって、求める直線はy=x+bであり、この式に(3,9)を代入します。
9=3+b
b=6
求める直線は、y=x+6
3-3:点Pのx座標が大きくなると、それにともなって小さくなるものを、次のア~エから1つ選び、その記号を書け。
ア 線分BQの長さ
イ ∠AOPの大きさ
ウ 直線BPの傾き
エ △BCQの面積
解答 : イ
解説 : ア 線分BQの長さ:tが大きくなると、BQは大きくなります。
イ 点Pが遠ざかるとき(tが大きくなるとき):線分OPの傾きはどんどん急になり、直線OAに近づいていきます。その結果、2つの線分OAとOPが作る△AOPの大きさは、小さくなります。
ウ 直線BPの傾き:m=t-2であり、tが大きくなると傾きは大きくなります。
エ △BCQの面積: 底辺BC(長さ 4)と高さ(QとBCのy座標の差9-4=5)が一定なので、面積は10で変わりません。
3-4:△PBCの面積が△ABQの面積の4/5となるとき、点Pのx座標を全て求めよ。
解答 : -1+√5 /2,1+√29 /2
解説 : 点Pのx座標をtとすると、点Pの座標は(t,t²)であり、A(-3,9)、B(-2,4)、C(2,4),Q(t,9)です。
△ABQの面積:
・底辺AQの長さはt-(-3)=t+3
・高さは9-4=5
△ABQ=1/2×(t+3)×5=5/2 (t+3)
△PBCの面積:
・底辺BCの長さは2-(-2)=4
・高さは|t²-4|
△PBC=1/2×4×|t²-4|=2|t²-4|
問題より、△PBC=4/5△ABQなので、
2|t²-4|=4/5×5/2(t+3)
2|t²-4|=2(t+3)
|t²-4|=t+3…①
点Cのx座標が2なので、Pのx座標tが2より小さいか大きいかで場合分けします。
[0
|t²-4|=-(t²-4)=4-t²
①は、
4-t²=t+3
t²+t-1=0

より、-1±√5 /2となります。
t>0であるため、t=-1+√5 /2
[t≧2のとき]
t²≧4なので、t²-4≧0です。
|t²-4|=t²-4
①は、
t²-4=t+3
t²-t-7=0
解の公式より、1±√29 /2
t≧2であるため、t=1+√29 /2
■大問4
右の図で、5点 A, B, C, D, Eは円Oの周上にある。線分CEは円Oの直径であり、AC⊥BDである。点Fは線分ACと線分BDとの交点であり、点Gは線分CEと線分BDとの交点である。各問いに答えよ。
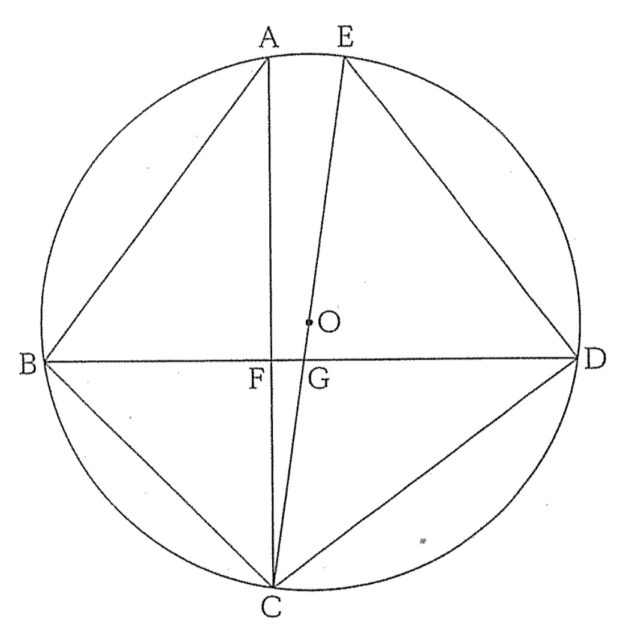
4-1:△ACF∽△ECDを証明せよ。
解答 : [証明](例)
△BCFと△ECDにおいて
仮定から∠BFC=90°…①
直径に対する円周角より∠EDC=90°…②
①、②より∠BFC=∠EDC…③
1つの弧に対する円周角は等しいから
∠CBF=∠CED…④
③、④より
2組の角がそれぞれ等しいから△BCF∽△ECD
解説 : △ACFと△ECDにおいて、相似条件「2組の角がそれぞれ等しい」を満たすことを示します。(以下解答と同じなので省略)
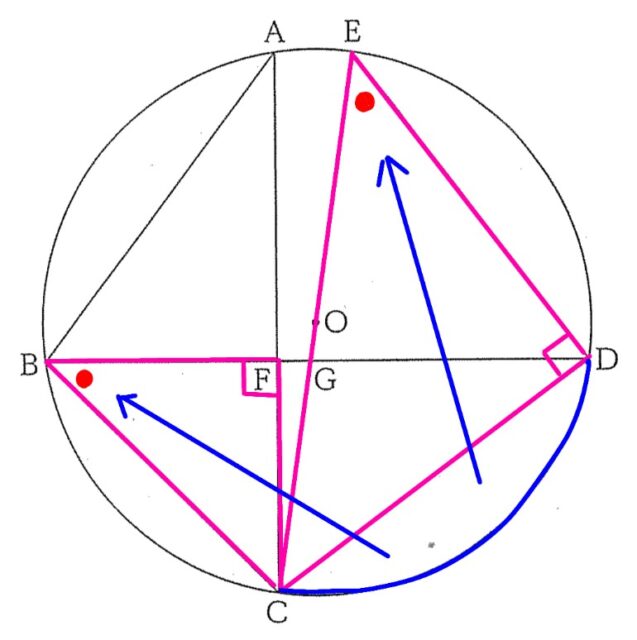
4-2:∠ABD=a°とするとき、∠BECの大きさをaを用いて表せ。
解答 : 90°-a°
解説 : 円周角の定理より、∠ABDと∠ACDは、どちらも弧ADに対する円周角なので、∠ACD=∠ABD=a°
点Fは線分ACとBDの交点であり、仮定よりAc⊥BDです。したがって、△FCDは∠CFD=90°の直角三角形です。
直角三角形の内角の和は180°ですから、
∠FDC+∠FCD=90°
ここで、∠FDCは∠BDCのことであり、∠FCDは∠ACDのことです。∠BDC+∠ACD=90°
∠ACD=a°を代入すると、
∠BDC+a°=90°
∠BDC=(90-a)°となります。
∠BECと∠BDCは、どちらも弧BCに対する円周角です。
∠BEC=∠BDC
∠BDC=(90-a)°を代入すると、
∠BEC=(90-a)°

∠DCE=45°, BC=6cm, CE=10cmのとき、①、②の問いに答えよ。
4-3①:線分AFの長さを求めよ。
解答 : 4√2cm
解説 : △ECDは、直角二等辺三角形なのでCD:ED:EC=1:1:√2より、CD=5√2cmです。
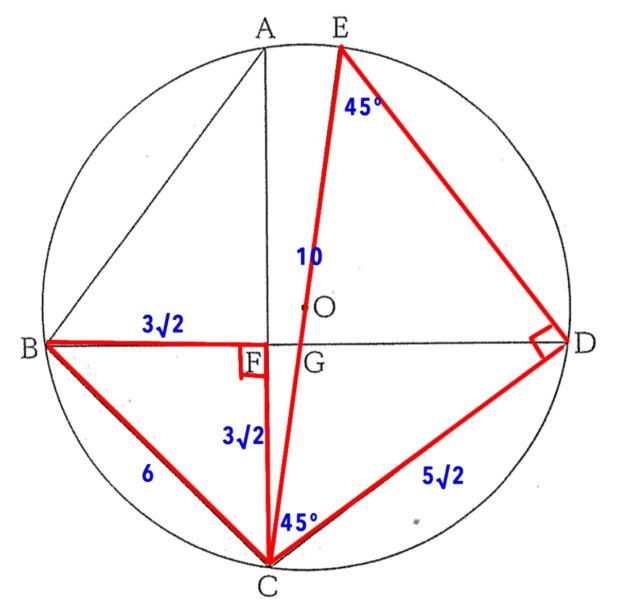
△BCFも直角二等辺三角形なのでBF=CF=3√2cmとなります。
問題の仮定より、∠AFB=∠DFC=90°
弧ADに対する円周角より、∠ABF=∠DCFであり、
BF=CFより、1辺と両端角が等しく△ABF≡△DCFとなります。
△DCFはFC:CD:DF=3:4:5なので、DF=AF=4√2
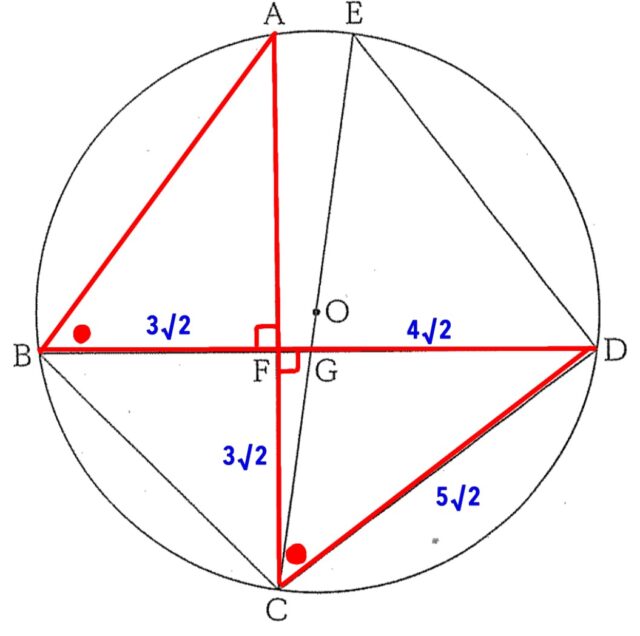
4-3②:点Oと線分BDとの距離を求めよ。
解答 : √2/2cm
解説 : △OBCは、OB=OD=半径=5cmなので、二等辺三角形です。
OからBDに垂線をおろした交点をHとすると、HはBDの中点となります。
HD=1/2BD=1/2(3√2+4√2)=1/2×7√2=7√2 /2cm
OとBDとの距離=OHです。
よって、三平方の定理
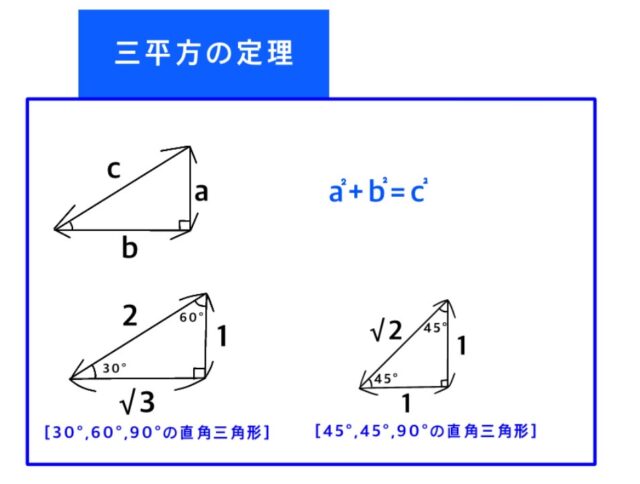
より、
OH=√2/2cm