2025年度大阪学力検査問題過去問【理科】

■問題PDF　

■目次　

■大問１

太陽や月などの天体の動きに興味をもったFさんは、数日後に日本の各地で日食が観測できることを知り、日食の当日に大阪市にある自宅近くで観測を行うことにした。次の問いに答えなさい

1-1:地球よりも太陽に近い軌道を公転している惑星は二つあり、そのうちの一つは金星である。もう一つは何か。惑星の名称を漢字2字で書きなさい。

解答 ： 水星

解説 ： 太陽系の惑星は、太陽に近い順から「水星、金星、地球…」です。地球よりも太陽に近い「内惑星」は水星と金星の二つです。

太陽は、地球から最も近い距離にある恒星である。太陽から放出された光や熱のエネルギーは、地球における大気の運動や生命活動に影響を与えている。

1-2①:黒点の温度は、太陽の表面の温度である約6000℃よりもa[ ア 低い イ 高い ]。黒点を数日間観測すると、黒点の位置が少しずつ一方向へ移動していくように見えるが、これはb[ ウ 地球の公転 エ 太陽の自転 ]が主な原因である。

解答 ： ア、エ

解説 ： 黒点は周囲（光球、約6000℃）よりも温度が低いために（約4000℃）黒く見えます。また、太陽自身が約27日の周期で自転しているため、黒点も一緒に移動して見えます。

1-2②:太陽と地球との距離は約1億5000万kmである。光の速さでは1億5000万kmの距離を進むのに何秒かかるか、求めなさい。ただし、光の速さは30万km/sであるものとする。

解答 ： 500 秒

解説 ： 時間を求めるには、「距離 ÷ 速さ」を計算します。1億5000万km ÷ 30万km/s = 500 秒。

【Fさんが日食について事前に調べたこと】
・日食は、太陽、月、地球の順に三つの天体が並び、地球から見たときに太陽が月で隠されることによって起こる現象である。
・日食が起こるのは、[ ア 新月 イ 満月 ウ 上弦の月 エ 下弦の月 ]のときである。
・今回の日食では、太陽の全部が隠されることはない。
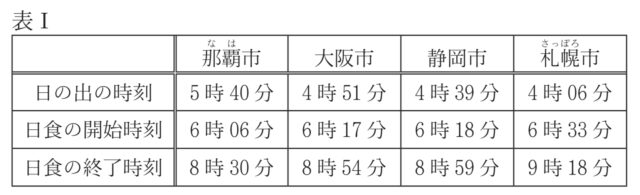
・表1 は、Fさんの自宅がある大阪市を含む4地点での、日の出の時刻、日食の開始時刻、日食の終了時刻をまとめたものである。

1-3:上の文中のc[ ]から適切なものを一つ選び、記号を○で囲みなさい。

解答 ： ア

解説 ： 日食は、太陽、月、地球がこの順に一直線に並び、月が太陽を隠す現象です。地球から見て太陽と同じ方向に月があるとき（見かけ上、月が太陽に重なるとき）を「新月」と呼びます。

1-4:表1から読み取れることについて述べた次の文中のd[ ]、e[ ]から適切なものをそれぞれ一つずつ選び、記号を○で囲みなさい。表1に示した4地点において、日の出の時刻が早いほど、日食の開始時刻や日食の終了時刻は d[ ア 早い イ 遅い ]。また、日食の開始から終了までの時間の長さは、4地点ですべて e[ ウ 同じである エ 異なる ]。

解答 ： イ、エ

解説 ： 表1を見ると、札幌市が最も日の出が早く（4:06）、日食の開始（6:33）・終了（9:18）も他の都市より遅くなっています。また、各都市の日食時間（終了時刻 – 開始時刻）を計算すると、すべて異なります。

1-5:日の出の時刻は日ごとに少しずつ変化する。次のア〜エのうち、大阪市での日の出の時刻の変化を表したグラフとして最も適しているものはどれか。一つ選び、記号を○で囲みなさい。

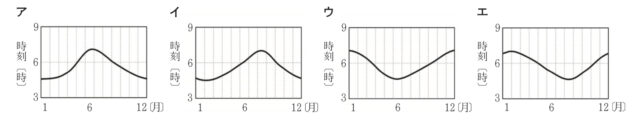
解答 ： ウ

解説 ： 北半球の日本では、夏至（6月下旬）の少し前に日の出が最も早くなり、冬至（12月下旬）の後に最も遅くなります（時刻の値が最大）。グラフ「ウ」がこの変化を示しています。

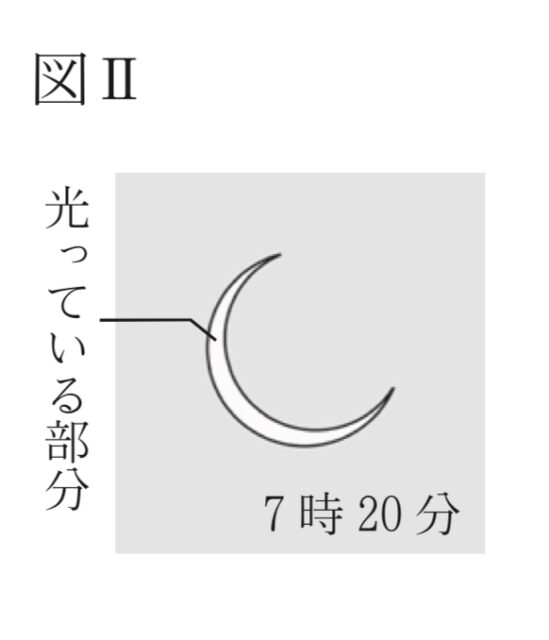
【観測】 Fさんは自宅近くで、図Iのように日食観測用のグラスを用いて、6時20分から日食の観測を行った。図IIは、Fさんが7時20分に観測した日食のようすを模式的に表したものである。(あ)この日、日本列島の近くを低気圧が通過したが、Fさんは雲が広がっていた時間帯でも、薄い雲を通して日食を観測することができた。

1-6:

解答 ： イ

解説 ： 低気圧は、中心の気圧が周囲より低い領域です。地表付近では、周囲から中心に向かって風が吹き込み、中心付近で上昇気流となります。上昇気流は雲を発生させやすいため、くもりや雨になりやすいです。

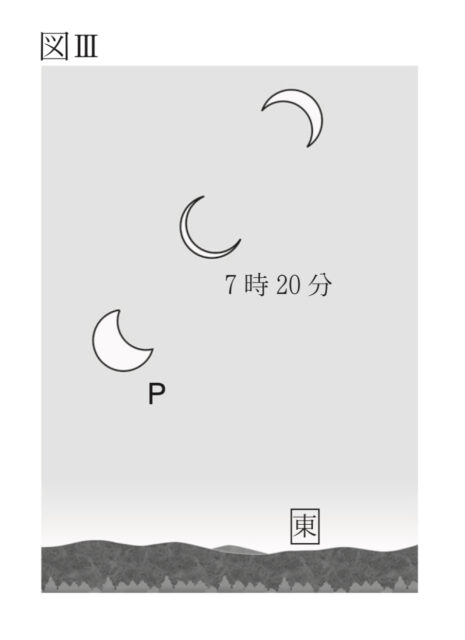
1-7:図Ⅲは、Fさんが6時50分、7時20分、7時50分に観測した日食のようすを模式的に表したものである。図Ⅲについて述べた次の文中のf[ ]、g[ ]から適切なものをそれぞれ一つずつ選び、記号を○で囲みなさい。

図中のPは、f[ ア 6時50分 イ 7時50分 ]の日食のようすを表したものである。図Ⅲから、太陽も月も日周運動によってほぼ同じ経路を移動していたことが分かり、また、太陽は月に比べて日周運動によって移動する速さが g[ ウ 遅かった エ 速かった ]ことが分かる。

解答 ： ア、エ

解説 ： ①図Ⅲでは、太陽が左下から右上へ移動しています。これは朝の時間帯の太陽の動き（東から昇り南へ向かう）を表しています。Pは3つの時刻のうち最も低い位置にあるため、最も早い時刻である「ア 6時50分」となります。 ② 図Ⅲでは、三つの太陽はほぼ同じ線上を動いています。これは「太陽も月も日周運動によってほぼ同じ経路を通っている」ことを表しています。しかし、時間がたつにつれて太陽の欠け方（どの側が欠けているか）が変化しています。これは、太陽と月の位置関係が少しずつずれていることを意味し、月が太陽に対して東向き（左向き）へ相対的に動いていることが分かります。同じ経路を通りながら、太陽の方が月よりも西（右）側へ先に進んでいくので、「日周運動によって移動する速さ」は太陽の方が月より速いと判断できます。よって （速かった） になります。

1-8:Fさんが日食の観測を行った日から2週間後、日本の各地で月食が観測された。次の文は、日食と月食の両方を観測したFさんが、日食や月食についてまとめたものである。文中の[ ]に入れるのに適している内容を、「地球」の語を用いて書きなさい。

日食は、太陽、月、地球の順に三つの天体が並び、地球から見て月が太陽と同じ向きにあるときに、太陽が月で隠されることによって起こる現象である。地球から見て太陽の全部が月で隠されると皆既日食となる。一方、月食は、太陽、地球、月の順に三つの天体が並び、地球から見て月が太陽と反対の向きにあるときに、月がhに入ることによって起こる現象である。地球から見て月の全部がhに入ると皆既月食となる。

解答 ： 地球のかげ

解説 ： 月食は、太陽、地球、月の順に一直線に並び、月が地球の影（本影）に入ることで暗く見える（または欠けて見える）現象です。

■大問２

家庭で複数の電気器具をコンセントにつないで使用するとき、それらの電気器具どうしは直列ではなく並列につながっている。このことに興味をもったSさんは、直列回路と並列回路の特徴を調べる実験をK先生と一緒に行い、考察した。次の問いに答えなさい。ただし、接続したモーターや抵抗器以外の電気抵抗は考えないものとし、モーターや抵抗器の電気抵抗は一定であるものとする。

2-1:右の図のような回路に電流が流れているとき、一の電気をもつ粒子が導線内を一極から+極の向きに移動している。このような一の電気をもつ粒子は何と呼ばれているか。漢字2字で書きなさい。

解答 ： 電子

解説 ： 電流の正体は、導線内を移動する「電子」と呼ばれるマイナス（一）の電気を帯びた粒子です。電子は一極から+極へ移動します（電流の向きとは逆）。

2-2:電源の一極側の導線を電流計の500mAの一端子につないで回路に電流を流したところ、電流計の針は図Iの位置を示した。次のア〜エのうち、図Iから読み取れる電流の大きさとして最も適しているものを一つ選び、記号を○で囲みなさい。

ア 3.40 mA イ 34.0 mA ウ 340 mA エ 3.40 A

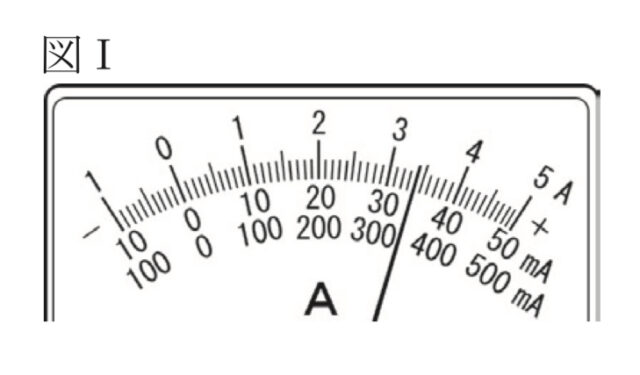
解答 ： ウ

解説 ： 電流計のマイナス端子を「500mA」につないだ場合、目盛りの最大値が500mAになるように読み取ります。図Iの針は「300」と「400」の間の、4つ目の目盛りを指しているので、340mA となります。

【実験1】同じ電気抵抗をもつ抵抗器を五つ用いて、図Ⅱと図Ⅲで表される二つの直列回路をつくった。それぞれの回路における電源の電圧を15Vに設定して30秒間電流を流した。電流計の示す値は、図Ⅱの回路では0.15A、図Ⅲの回路では 0.10Aであった。

【実験2】実験1で使用した抵抗器を五つ用いて、図IVと図Vで表される二つの並列回路をつくった。それぞれの回路における電源の電圧を15Vに設定して30秒間電流を流した。電流計の示す値は、図IVの回路では0.60A、図Vの回路では0.90Aであった。

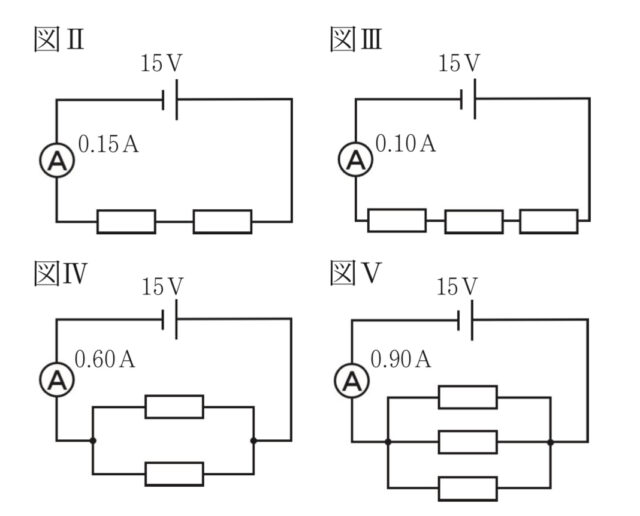
2-3:次のア〜エのうち、回路図にしたときに図IVと同じ回路図になるものはどれか。最も適しているものを一つ選び、記号を○で囲みなさい。

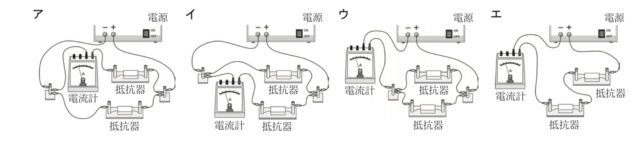
解答 ： ウ

解説 ： 図IVは、電源、電流計（全体を測定）、および2つの抵抗器が並列に接続された回路です。選択肢エも、電源、電流計（全体を測定）、そして2つの並列接続された抵抗器で構成されており、図IVと全く同じ回路図を表しています。

【各抵抗器に加わる電圧と各抵抗器を流れる電流について】 表1は、実験1と実験2において、各抵抗器に加わる電圧と各抵抗器を流れる電流について、Sさんがまとめたものである。

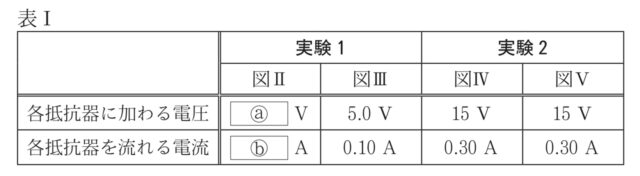
2-4:表1中の [ a ]、[ b ] に入れるのに適している数をそれぞれ書きなさい。

解答 ： a: 7.5 (V), b: 0.15 (A)

解説 ： 図IIは直列回路です。a: 電源の電圧（15V）が2つの同じ抵抗器に均等に分けられるため、15V ÷ 2 = 7.5V。 b: 直列回路では電流はどこでも同じため、電流計が0.15Aなら各抵抗器にも0.15Aが流れます。

【SさんとK先生の会話】
K先生: 実験1と実験2のそれぞれにおいて、抵抗器の数が多くなったときの、各抵抗器によって消費される電力の変化について考えてみましょう。
Sさん: (あ)各抵抗器を直列につないだ実験1とは違って、各抵抗器を並列につないだ実験2においては、各抵抗器によって消費される電力は図IVの回路と図Vの回路で変わりません。
K先生: その通りです。家庭の電気器具が並列につながっているのは、並列回路には電気器具の数が変わっても、電気器具一つ一つで消費される電力は一定で変わらないという利点があるからです。
Sさん: そうか、電球の明るさは、消費される電力によって変わります。電球が明るくなったり暗くなったりして、明るさが安定していないと困りますものね。家庭の電気器具が並列につながっている理由がよく分かりました。
K先生: それは良かったです。しかし、並列回路には回路の一部に大きな電流が流れる危険性もあります。家庭では複数の電気器具を同時に使用することがよくあるため、(い)回路に大きな電流が流れた場合、安全のために電流の流れを止める装置があります。同時に使用する電気器具の数が多くなりすぎて、回路に大きな電流が流れることがないように注意しましょう。

2-5:下線部あについて、次の文中の [c] に入れるのに適している数を求めなさい。答えは整数で書くこと。

実験1の図Ⅲの回路と実験2の図Vの回路では抵抗器の数はどちらも三つで同じであるが、図Ⅲの回路で各抵抗器によって消費される電力は、図Vの回路で各抵抗器によって消費される電力の [c] 分の1である。

解答 ： 9 (分の1)

解説 ： 電力(W) = 電圧(V) × 電流(A)。 [図Ⅲ]各抵抗器の電力 = (15V ÷ 3) × 0.10A = 5.0V × 0.10A = 0.5W。 [図V]各抵抗器の電力 = 15V × (0.90A ÷ 3) = 15V × 0.30A = 4.5W。 [比較] 0.5W ÷ 4.5W = 1/9。

2-6:電気器具によって消費される電気エネルギーの量を電力量という。次の文は、実験1と実験2において各抵抗器によって消費される電力量について述べたものである。文中の [d] に入れるのに適している内容を、「電流」の語を用いて書きなさい。

電力量は、消費される電力と [d] によって決まる。実験1と実験2においては [d] 同じであったので、図Ⅲの回路で各抵抗器によって消費される電力量と、図Vの回路で各抵抗器によって消費される電力量の大小を比較するためには、各抵抗器によって消費される電力の大小のみを比較すればよい。

解答 ： 電流を流す時間

解説 ： 電力量（J）は、消費された電気エネルギーの総量を示し、「電力（W）× 時間（秒）」で計算されます。問題文の指示（「電流」の語を用いる）に基づき、「電流を流す時間」と解答します。

2-7:下線部いについて、25Ωの電気抵抗をもつ抵抗器が五つ、図VIのように並列につながっている。仮に図VI中のP点を流れる電流が15Aを超えた場合、P点で回路が途切れるようになっている。図VIの回路について述べた次の文中の [e]、[f]に入れるのに適している数をそれぞれ書きなさい。ただし、電源の電圧は100Vであるものとする。

図VIの回路において、P点を流れる電流を15A以下にするためには、5箇所のスイッチのうち、スイッチを同時に入れている箇所を最大で [ e ] 箇所までにしなければならない。スイッチを同時に入れている箇所が [ e ] 箇所あるとき、P点を流れる電流は [ f ] Aとなる。

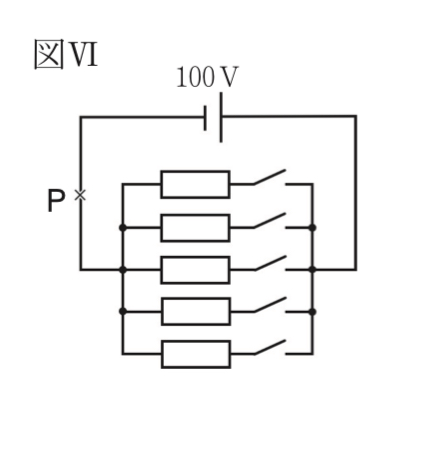
解答 ： e 3 (箇所), f 12 (A)

解説 ： 抵抗器1つ（スイッチ1箇所）あたりの電流は、オームの法則より 100V ÷ 25Ω = 4A です。P点を流れる電流を15A以下にするには、4A × N 箇所 ≦ 15A を満たす必要があります。N ≦ 3.75 なので、最大の整数Nは「3」です（e）。その時の電流は 4A × 3箇所 = 12A です（f）。

■大問３

生物の種類の多様性は、進化によって生物が長い年月をかけて変化してきたことで生じたものである。このことに興味をもったTさんは、進化による生物のからだの変化について調べ、R先生と一緒に考察した。次の問いに答えなさい。

3-1①:次のア〜ウのうち、一般に、核のほかに動物の細胞と植物の細胞に共通してみられるつくりはどれか。最も適しているものを一つ選び、記号を○で囲みなさい。
ア 葉緑体 イ 細胞膜 ウ 細胞壁

解答 ： イ

解説 ： ア(葉緑体)とウ(細胞壁)は植物の細胞に特有です。イ(細胞膜)は細胞の内外を仕切る膜で、動物・植物ともに共通して存在します。

3-1②:

解答 ： カ (① DNA, ② 染色体)

解説 ： 遺伝子の本体は DNA（デオキシリボ核酸）です。DNAは通常、核の中でタンパク質と結合し、「染色体」という構造をとっています。

地球の長い歴史を、生物の移り変わりなどをもとに区分したものを地質年代という。

3-2①:

解答 ： エ (① 中生代, ② 約2億5000万年前~約6600万年前)

解説 ： 恐竜やアンモナイトは「中生代」です。中生代は約2億5000万年前から約6600万年前までの期間を指します。

3-2②:進化によってさまざまな種類の生物が出現してきた一方で、絶滅した生物もいる。アンモナイトは、すでに絶滅し現在は存在していないが、イカやタコなどと同じ軟体動物であることが分かっている。軟体動物に共通してみられる、内臓を包む膜は何と呼ばれる膜か、書きなさい。

解答 ： 外とう膜

解説 ： アンモナイトやイカ、タコ、貝類などが含まれる軟体動物は、内臓が「外套膜（がいとうまく）」と呼ばれる膜で覆われているのが特徴です。

【Tさんが進化による生物のからだの変化について調べたこと】 ・現在の見かけの形やはたらきは異なっていても、基本的な内部のつくりが同じで、起源は同じであったと考えられる器官は [ e ] 器官と呼ばれており、生物が進化してきた証拠の一つと考えられている。 ・クジラやイルカのひれとコウモリの翼は、基本的な骨格のつくりから [ e ] 器官であると考えられており、それぞれ進化によって長い年月をかけて生息する環境に都合の良い形に変化してきたと考えられている。

3-3:上の文中の [ e ] に入れるのに適している語を書きなさい。

解答 ： 相同 (器官)

解説 ： 現在の形や働きは異なっていても（例：クジラのひれとコウモリの翼）、元々は同じ器官から進化したと考えられる器官を「相同器官」と呼びます。

3-4:地球の長い歴史の中で、動物だけでなく植物も進化してきた。次の文中の[ f ] に入れるのに適している語を書きなさい。陸上では、コケ植物やシダ植物のように、[ f ] のうと呼ばれる袋をもち、この袋の中にある [ f ] によってふえるなかまが出現した後で、裸子植物や被子植物のように種子によってふえるなかまが出現したと考えられている。

解答 ： 胞子

解説 ： コケ植物やシダ植物は、種子ではなく「胞子」で増えます。胞子が入っている袋を「胞子のう」と呼びます。

【TさんとR先生の会話1】
Tさん: 植物にも、見かけの形が異なっていても内部のつくりが同じ器官はあるのでしょうか。
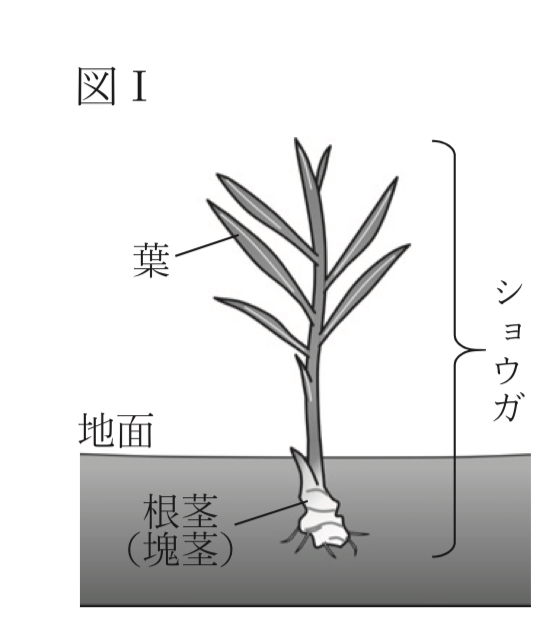
R先生: はい。植物にもそのような器官はあります。ショウガという被子植物には、図Iに示されているように、「根茎(塊茎)」と呼ばれる器官があります。根茎は地下にあり根のように見えますが、根ではなく茎の一種です。ショウガの根茎と一般的な植物の茎は基本的な内部のつくりが同じです。
Tさん: 根茎の見かけの形からはまったく分かりませんでした。実際にショウガの根茎の内部のつくりを観察してみたいと思います。

3-5:ショウガはジャガイモなどと同じように無性生殖でふえることができる植物であり、根茎を切り分けて土に植えると、根茎から芽が出て新しい個体となる。無性生殖について述べた次の文中のg[ ]、h[ ]から適切なものをそれぞれ一つずつ選び、記号を○で囲みなさい。

一般に、無性生殖では、g[ ア 減数分裂 イ 体細胞分裂 ] によって親のからだの一部が新しい個体(子)となり、子の形質は親と h[ ウ 同じ形質 エ 異なる形質 ] になる。

解答 ： イ、ウ

解説 ： 無性生殖（例：ジャガイモの芽）は、親の体の一部が「体細胞分裂」によって増えて新しい個体となります。遺伝情報がそのままコピーされるため、子の形質は親と全く同じになります。

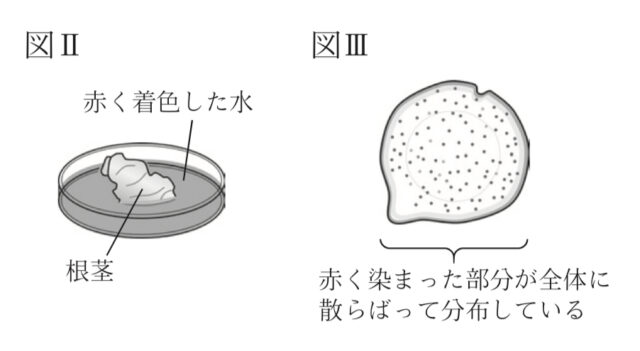
【実験】図Ⅱのように、ショウガの根茎の下部を切り取り、切り口の面を赤く着色した水に約6時間つけた後、切り口の面と平行に複数の部分に切り分けた。その結果、複数の部分に切り分けたときにできた断面にはどれも、赤く染まった部分が全体に散らばって分布しているようすが観察された。図Ⅲは、根茎を複数の部分に切り分けたときにできた断面の一つをスケッチしたものである。

【TさんとR先生の会話2】
Tさん: 図Ⅲ中の赤く染まった部分は、根茎に吸わせた赤く着色した水が通った場所だと考えられるので、[ X ] でしょうか。
R先生: はい。図Ⅲのように、ショウガの根茎には [ X ] が散らばって分布しているというつくりがあることが分かります。このようなつくりをこれまでに見たことはありませんか。
Tさん: 図Ⅲのようなつくりは、[ Y ] と共通しています。このことから、ショウガの根茎は単子葉類の茎の一種であるといえそうです。
R先生: その通りです。生物のある器官について、見かけの形や内部のつくりなどを調べることは、生物の進化を考える上でとても大切なことです。

3-6:

解答 ： X: イ, Y: カ

解説 ： d: 赤く着色した水（根から吸い上げた水）が通る管は「道管」です。 e: 維管束（道管・師管の束）が「全体に散らばって分布」しているのは、「単子葉類」（トウモロコシやツユクサなど）の茎の特徴です。

■大問４

理科の授業で、水溶液の温度を下げたときに結晶が出てくることを観察したYさんは、溶解度や再結晶について調べ、N先生と一緒に硝酸カリウム水溶液を用いた実験を行った。次の問いに答えなさい。

【Yさんが溶解度や再結晶について調べたこと】
・一定量の水に物質をとかして飽和水溶液にしたときに、とけた物質の質量の値を溶解度という。一般に、溶解度は水100gにとける物質の最大の質量 [g] で表す。
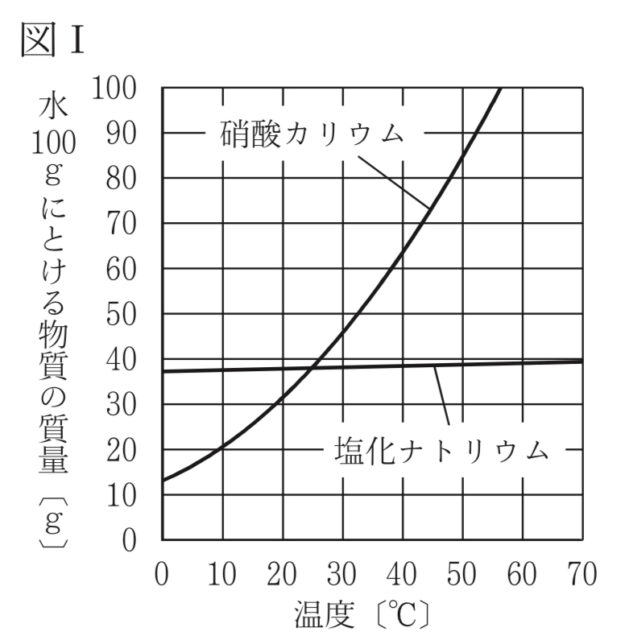
・(あ)硝酸カリウムや塩化ナトリウムの溶解度曲線は、図1のようになる。
・固体の物質をいったん水などの溶媒にとかし、再び結晶として取り出すことを再結晶という。

4-1:硝酸カリウム水溶液のように、いくつかの物質が混ざり合ってできているものを混合物という。ア~エのうち、混合物であるものはどれか。一つ選び、記号を○で囲みなさい。

ア 空気 イ 塩化ナトリウム ウ 水 エ 銅

解答 ： ア

解説 ： 混合物とは、2種類以上の物質が混ざり合ったものです。「空気」は窒素、酸素、二酸化炭素などが混ざった混合物です。イ、ウ、エは純物質です。

4-2①:下線部あについて、硝酸カリウムや塩化ナトリウムは水の中で電離する。次のア~エのうち、塩化ナトリウムの電離のようすを表した式として最も適しているものはどれか。一つ選び、記号を○で囲みなさい。

ア NaCl → Na^2- + Cl^2+
イ NaCl → Na^- + Clz^+
ウ NaCl → Na^2+ + Cl^2-
エ NaCl → Na^+ + Cl^-

解答 ： エ

解説 ： 塩化ナトリウム（NaCl）は水に溶けると、陽イオンである「ナトリウムイオン（Na+）」と、陰イオンである「塩化物イオン（Cl-）」に分かれます（電離）。

4-2②:硝酸カリウムや塩化ナトリウムのように、水にとかしたときに、その水溶液に電流が流れる物質は、一般に何と呼ばれているか。漢字3字で書きなさい。

解答 ： 電解質

解説 ： 硝酸カリウムや塩化ナトリウムのように、水に溶けて電離し、その水溶液が電気を通す物質を「電解質」と呼びます。

4-3:次の文は、図1の溶解度曲線から分かることを述べたものである。文中の a[ ]、b[ ] から適切なものをそれぞれ一つずつ選び、記号を○で囲みなさい。

図から、50℃の水100gにとける硝酸カリウムの最大の質量はa[ ア 約75g イ 約85g ウ 約95g ] であることが分かる。また、図1から、硝酸カリウムと塩化ナトリウムの溶解度が等しいときの温度はb[ エ 約15℃ オ 約25℃ カ 約35℃ ] であることが分かる。

解答 ： イ、オ

解説 ： グラフ（図1）を読み取ります。① 50℃の線と「硝酸カリウム」の曲線が交わる点は、80gと90gの間の85gに近いです。② 2本の曲線が交わっている点の温度は、20℃と30℃の間の25℃に近いです。

4-4:図1における硝酸カリウムと塩化ナトリウムの溶解度について述べた次の文中の [c]、[d] に入れるのに適している語の組み合わせを、あとのア〜エから一つ選び、記号を○で囲みなさい。

水100gが入った容器を二つ用意し、一方には硝酸カリウムを、もう一方には塩化ナトリウムをとかして40℃の飽和水溶液をつくり、それぞれの容器にふたをした。これらの40℃の飽和水溶液をそれぞれ10℃まで冷やした場合、冷やしたことで出てくる結晶の質量は、[ c ] の飽和水溶液の方が小さいと考えられる。これは、硝酸カリウムと塩化ナトリウムを比較した場合、[ c ] の方が温度の変化にともなう溶解度の変化が [ d ] ためである。

ア c:硝酸カリウム, d:小さい
イ c:硝酸カリウム, d:大きい
ウ c:塩化ナトリウム, d:小さい
エ c:塩化ナトリウム, d:大きい

解答 ： ウ

解説 ： グラフ（図1）を見ると、硝酸カリウムの曲線は急な坂（温度による変化が大きい）ですが、塩化ナトリウムの曲線はほぼ水平（温度による変化が小さい）です。そのため、冷やしても溶解度の差が小さい塩化ナトリウムの方が出てくる結晶は少ないです。

【YさんとN先生の会話1】 N先生: 硝酸カリウム水溶液は無色透明なので、濃度が異なっていても見かけだけでは濃度の違いは分かりません。硝酸カリウム水溶液の濃度の違いを確かめるには、どのような方法があると思いますか。 Yさん: 硝酸カリウム水溶液を冷やしていくとよいと思います。水溶液の濃度が異なれば、冷やしていった際に、結晶が出始める温度に差が出るのではないでしょうか。 N先生: では、実際に質量パーセント濃度の異なるいくつかの硝酸カリウム水溶液を用意し、それぞれ冷やして結晶が出始める温度を調べてみましょう。

【実験1】図Ⅱのような四つの容器A、B、C、Dを用意した。容器A〜Dに、質量パーセント濃度の異なる40℃の硝酸カリウム水溶液を100gずつ入れ、それぞれふたをして氷水につけた。容器A〜Dの水溶液の温度を、それぞれ40℃から10℃まで冷やしていく過程で、結晶が出始めた水溶液の温度を記録した。表1は、その結果をまとめたものである。

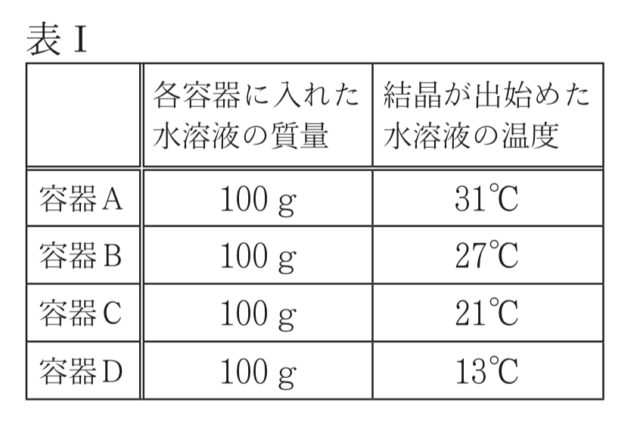
Yさんは、水溶液の質量パーセント濃度や、再結晶で出てくる結晶の質量を、溶解度を用いて求めることにした。次の問いに答えなさい。ただし、水100gにとける硝酸カリウムの最大の質量は、31℃では47g、27℃では41g、21℃では33g、13℃では24gであるものとする。

4-5①:実験1において、容器Aの水溶液の温度が40℃のとき、容器Aの水溶液の質量パーセント濃度は何%であると考えられるか、求めなさい。答えは小数第1位を四捨五入して整数で書くこと。

解答 ： 32 (%)

解説 ： 容器Aは「31℃で結晶が出始めた」とあるので、31℃で飽和水溶液になったことを意味します。31℃での溶解度は47g（水100gに硝酸カリウム47g）です。濃度 = (溶質47g ÷ 溶液(47g+100g)) × 100 = (47 ÷ 147) × 100 ≒ 31.97…%。四捨五入して32%となります。

4-5②: 実験1において、容器Bの水溶液の温度が13℃のとき、容器Bの水溶液の中には何gの硝酸カリウムの結晶が出ていると考えられるか、求めなさい。答えは小数第1位を四捨五入して整数で書くこと。

解答 ： 12 (g)

解説 ： 容器Bは27℃（溶解度41g）の飽和水溶液です。実験に使った溶液100gに含まれる水と溶質を計算します。水: 100g × (100 / (100+41)) ≒ 70.92g。 溶質: 100g × (41 / (100+41)) ≒ 29.08g。 この溶液を13℃（溶解度24g）まで冷やすと、水70.92gに溶けることができる溶質は 24g × (70.92g / 100g) ≒ 17.02g。 したがって、出てくる結晶は 29.08g – 17.02g ≒ 12.06g。四捨五入して12gです。

【YさんとN先生の会話2】
Yさん: 実験1では、水溶液の濃度が異なれば、予想していた通り結晶が出始める水溶液の温度に差が出ました。ところで、表1から考えると、容器Aの水溶液の中に結晶があるなら、そのときの水溶液の温度は、31℃よりも低いといえますよね。
N先生: はい。水溶液の中にとけきれなくなった結晶が十分にあるなら、そのときの水溶液の温度は、表1に示された結晶が出始めた温度よりも低いと考えてよいですよ。
Yさん: 容器A~Dを室内に置いておくと、水溶液の温度は、やがて室温と等しくなるのでしょうか。
N先生: 急な温度変化のない室内にしばらく置いた後であれば、水溶液の温度と室温は等しいと考えてよいですよ。
Yさん: ということは、容器Aだけでなく、同時に容器B~Dについても水溶液の中の結晶の有無を確認することで、そのときのおおよその室温を推定できるのではないでしょうか。
N先生: おもしろい考えですね。では実際に、容器A~Dを実験室に数日間置いた後に、水溶液の中の結晶の有無を確認して、そのときのおおよその実験室の室温を推定してみましょう。

【実験2】容器A~Dを、ふたをしたまま実験室に数日間置いた後に、よく振ってから水溶液のようすを観察した。その結果、容器Aおよび容器Bの水溶液の中にはとけきれなくなった結晶が十分にあり、容器Cおよび容器Dの水溶液の中には結晶がなかった。

実験2について述べた次の文中のe[ ]、f[ ]から最も適切なものをそれぞれ一つずつ選び、記号を○で囲みなさい。ただし、容器A~Dの水溶液の温度と実験室の室温は等しいものとする。

容器Aおよび容器Bの水溶液の中には結晶があったことから、どちらの水溶液も飽和していたことが分かる。したがって、容器Aおよび容器Bの水溶液の質量パーセント濃度は e[ ア 容器Aの水溶液の方が高い イ 容器Bの水溶液の方が高い ウ 等しい ] と考えられる。また、容器A~Dの水溶液のようすを観察したときの実験室の室温は、表1からf[ エ 31℃よりも低く27℃よりも高い オ 27℃よりも低く21℃よりも高い カ 21℃よりも低く13℃よりも高い キ 13℃よりも低い ] と推定できる。

解答 ： ウ、オ

解説 ： e[ ] 容器AもBも「とけきれなくなった結晶が十分にある」状態、つまりどちらもその温度での「飽和水溶液」です。同じ物質（硝酸カリウム）の飽わ水溶液の濃度は、温度が同じ（室温）であれば等しくなります。
f[ ] A(31℃)、B(27℃)には結晶があり、C(21℃)、D(13℃)には結晶がありません。これは、室温が「Cが飽和する21℃」よりは高く（だからCは溶けきった）、「Bが飽和する27℃」よりは低い（だからBは溶けきれず結晶が残った）ことを意味します。