■問題PDF
令和7年度_学力検査問題過去問【愛知】- 数学
■目次
大問１
大問２
大問３
■大問１
問題１-１：6+10÷(-2) を計算した結果として正しいものを、 次のアからエまでの中から一つ選びなさい。
ア -8 イ 1 ウ 8 工 11
解答 ： イ 1
解説 ： 6+10÷(-2)=6+(-5)=6-5=1
・掛け算(10÷(-2)の部分)から先に計算する。
問題１-２ ： 3(2x+3)-2(x-3) を計算した結果として正しいものを、次のアからエまでの中から一つ選びなさい。
ア 4x イ 4x+3 ウ 4x+6 エ 4x+15
解答 ： エ 4x+15
解説 ： 3(2x+3)-2(x-3)=3×2x+3×3 -2×x-2×(-3)
=6x+9-2x+6=(6-2)x+9+6=4x+15
・分配法則を使う。カッコの前の3を2xと3に、-2をxと-3にそれぞれ掛け算する。
問題１-３ ： 69/√3+√2×√6 を計算した結果として正しいものを、 次のアからエまでの中から一つ選びなさい。
ア 3√3 イ 5√3 ウ 5√6 エ 3√30
解答 ： イ 5√3
解説 ： 9/√3+√2×√6=(9×√3)/√3×√3+√2×6=9√3/√3²+√12=9√3/3+2√3=3√3+2√3=5√3
・9/√3は有理化。
・9/√3を足すのは後で、√2×√6の計算(掛け算)を優先して計算する。
問題１-４ ： 方程式x(x+4)=-3(x+1) の解として正しいものを、次のアからエまでの中から一つ選びなさい。
ア -7±√37 / 2 イ -7±√61 / 2 ウ 7±√61 / 2 エ 7±√37 / 2
解答 ：ア -7±√37 / 2
解説 ： x×x+x×4=-3×x-3×1 →x²+4x=-3x-3 →x²+4x+3x+3=0 →x²+7x+3=0
→x=(-7±√7²-4×1×3) / 2×1 →x=(-7±√49-12) / 2 →x=(7±√37) / 2
・分配法則や移行を使って整理する。
・因数分解できないので、解の公式を使う。
問題１-５ ： ある飲食店の来店者数は、11月は10月より30％増加し、12月は11月より20％増加した。また、12月の来店者数は、10月の来店者数より2800人多かった。このとき、10月の来店者数として正しいものを、次のアからエまでの中から一つ選びなさい。
ア 4200人 イ 4368人 ウ 5000人 工 5600人
解答 ：ウ 5000人
解説 ： 式を立てるポイントは3つ。
①11月=10月ひと月分+10月の30%分→11月=10月×(1+0.3)=→11月₌10月×1.3
②12月=11月ひと月分+11月の20%分→12月=11月×(1+0.2)→12月₌11月×1.2
③12月₌10月+2800(人)
②と③を組み合わせて、
10月+2800₌12月₌11月×1.2 よって、10月+2800₌11月×1.2…④
(12月の来場者数は10月、11月それぞれの来場者との関係から表せる)
10月と11月の来店者をそれぞれｘ、yとおく。
①11月₌10月×1.3 → y=x×1.3 → y=1.3x
④10月+2800₌11月×1.2 → x+2800=y×1.2 →x+2800=1.2y
2つの式で連立方程式を解く。
・y=1.3x (上)
・x+2800=1.2y (下)
下の式に、y=1.3xを代入して、x+2800=1.2×1.3x
→x+2800=1.56x →x=5000
10月の来場者をxとおいたので、10月の来場者数は5000人。
問題１-６ 2直線y=x-3、y=-2x-6の交点を通り、直線y=2x+1に平行な直線の切片として正しいものを、次のアからエまでの中から一つ選びなさい。
ア -4 イ -2 ウ 0 エ 4
解答 ：イ -2
解説 ： ・y=x-3、y=-2x-6の交点を通るので、2つの式で連立方程式。
x-3=-2x-6 →x=-1、y=-4 (-1, -4)
・直線が平行なときは、傾きの部分が等しいので、y=2x+1と平行な直線は、傾きが2だとわかる。
→ここで、一次関数の基本の式「y=ax+b」の傾きに2を代入。→ y=2x+b
y=2x+bに(-1, -4)を代入して、
-4=2×(-1)+b →b=-2
問題１-７ ： 関数y=-6/xのグラフについて正しく述べた文を、 次のアからカまでの中から二つ選びなさい。
ア 原点を対称の中心として点対称である。
イ x軸を対称の軸として線対称である。
ウ x軸と交わる。
エ y軸と交わる。
オ 関数y=xのグラフと2点で交わる。
カ 関数y = x 2 のグラフと2点で交わる。
解答 ：ア・オ
解説 y=6/xは、式から反比例だとわかる。
グラフを見ながら考えると、
原点を対象の中心として点対象になっているので、アは正しい。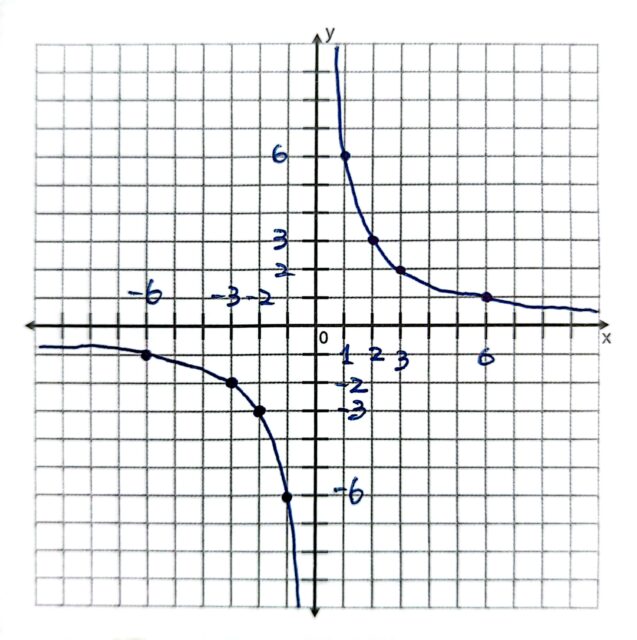
x軸を対象の軸として線対称とは言えないので、イは正しくない。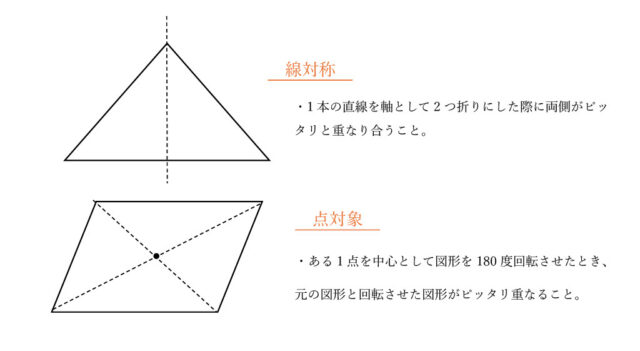
x軸ともy軸とも交わらないので、ウとエは不適当。
y=xのグラフと2点で交わると言えるので、オは正しい。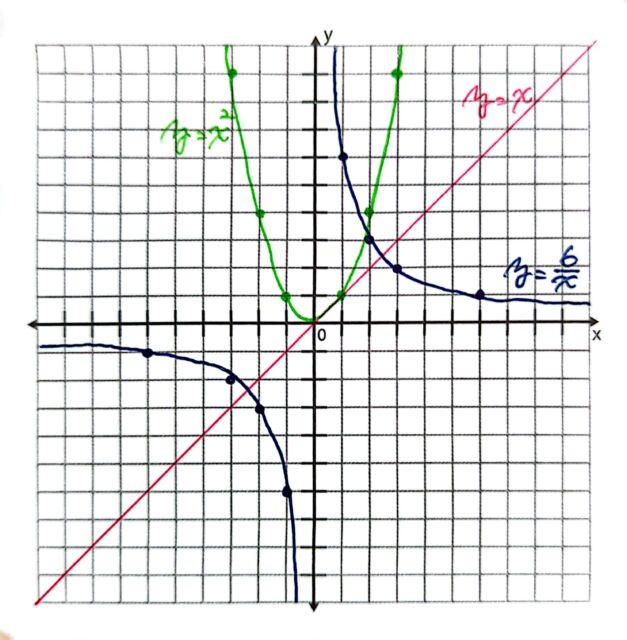
y=x²のグラフとは1点では交わるが、2点ではないので不適当。
以上より、答えは アとオ。
問題１-８：表は、あるキャベツ農園でとれたキャベツ8000個から無作為に抽出した50個のキャベツに対して、1個あたりの重さを調べ、その結果を度数分布表にまとめたものである。この農園でとれたキャベツ8000個のうち、重さが0.7 kg以上1.3 kg未満のキャベツの個数はおよそ何個と推定されるか、正しいものを次のアからエまでの中から一つ選びなさい。
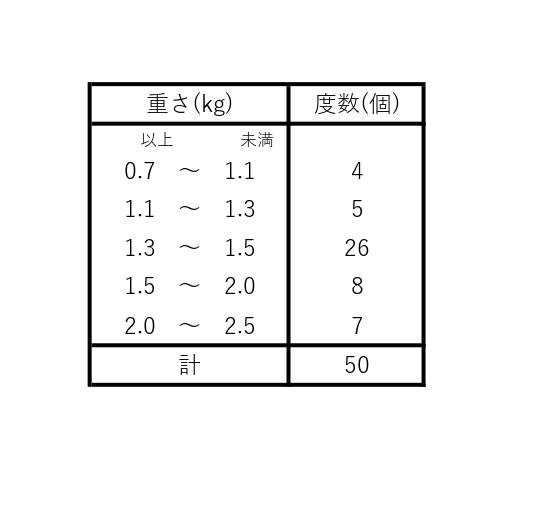
ア およそ640個 イ およそ800個 ウ およそ1440個 エ およそ5600個
解答 ： ウ およそ1440個
解説 ： 表を見ると、重さが0.7㎏以上1.3㎏未満のキャベツは、0.7㎏以上1.1㎏未満の階級の度数と1.1㎏以上1.3㎏未満の階級の度数を足すことで分かる。4+5=9となり、0.7㎏以上1.3㎏未満のキャベツは50個のうち9個あったことがわかる。
よって、9/50の割合で0.7㎏以上1.3㎏未満のキャベツが含まれている。
同様に、8000個の中にも9/50の割合で0.7㎏以上1.3㎏未満のキャベツが含まれていると想定できるので、8000×9/50=1440 となり、およそ1440個含まれているとわかる。
問題１-９ ： 箱の中にAが書かれているカードが3枚、Bが書かれているカードが2枚、Cが書かれているカードが1枚入っている。中を見ないで、この箱からカードを同時に2枚取り出す。取り出した2枚のカードに書かれた文字が異なる確率として正しいものを、次のアからエまでの中から一つ選びなさい。
ア 4/15 イ 7/18 ウ 11/18 エ 11/15
解答 ：エ 11/15
解説 ： 樹形図をかいて考える。
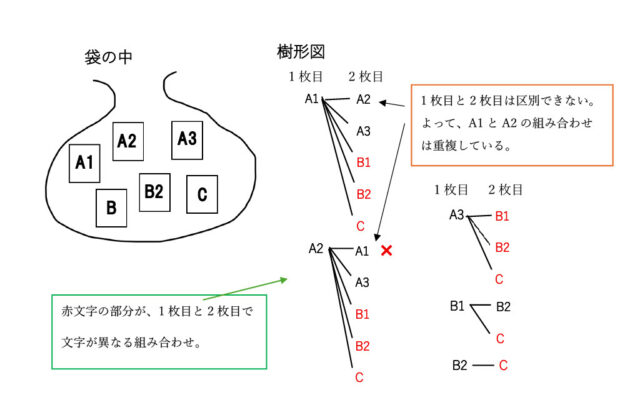
また、Ａの3枚と、B2枚は区別をつけて考える。
樹形図より、2枚の組み合わせは全部で15通り。
そのうち、2枚のカードに書かれた文字が異なるのは11通り。
よって、取り出した2枚のカードに書かれた文字が異なる確率は11/15となる。
問題１-１０ ： 図で、Eは線分ACとDBの交点、∠BAE= 36°、∠AED= 82°、∠EBC=50°、∠ECD=46°である。このとき、∠DAEの大きさとして正しいものを、次のアからエまでの中から一つ選びなさい。
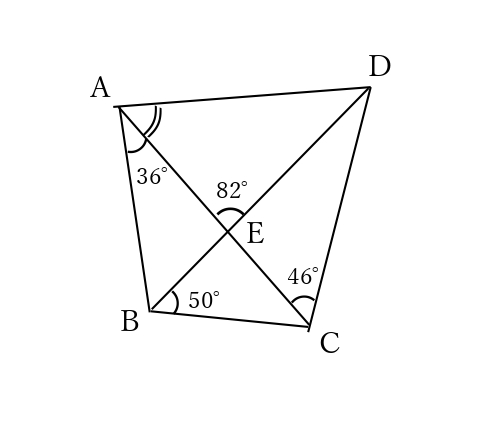
ア 46° イ 48° ウ 49° エ 50°
解答 ：エ 50°
解説 ：
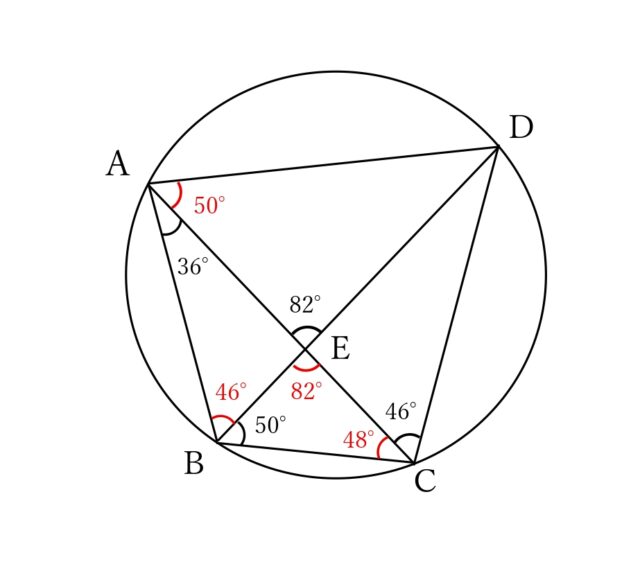
対頂角なので、∠BEC=82°
△BECの内角に着目して、∠ACB=180°-(82°+50°)=180°-132°=48°
△ACBに着目して、∠ABE=180°-(36°+50°+48°)=180°-134°=46°
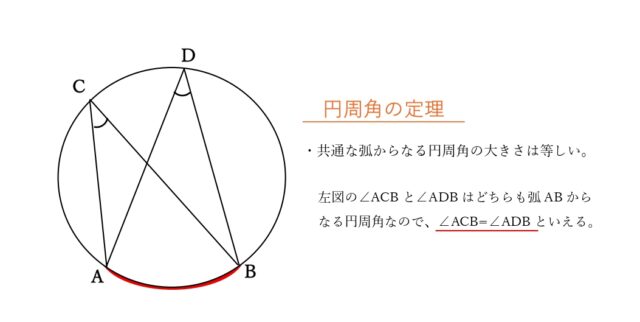
ここで、∠ABD(∠ABE)=∠ACD=46°となるので、∠ABDと∠ACDは共通の弧ADからなる円周角だとわかる。よって、四角形ABCDは円に内接していると言える。
同じく円周角の定理を活用して、求めたい∠DAE(∠DAC)は弧DCからなる円周角であり、同じく弧DCからなる他の円周角(∠DBC=50°)と等しくなるので、∠DAE=50°。
■大問２
問題２-１：
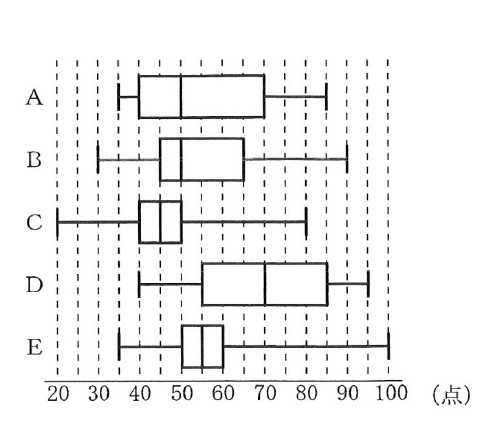
「音楽」「スポーツ」「文化」「歴史」「科学」の各分野100点満点、合計500点満点のクイズ大会に40人が参加した。
図は、このクイズ大会を行ったときの各分野の得点を、箱ひげ図で表したものであり、AからEは、音楽、スポーツ、文化、歴史、科学のいずれかを示している。
各分野の得点が、次の①から④までのとき、B、Dに当てはまる分野の組み合わせとして正しいものを、下のアからクまでの中から一つ選びなさい。
ア B：音楽 D：歴史 イ B：音楽 D：スポーツ
ウ B：スポーツ D：科学 エ B：スポーツ D：文化
オ B：文化 D：科学 カ B：文化 D：歴史
キ B：歴史 D：スポーツ ク B：歴史 D：文化
解答 ：ア B：音楽 D：歴史
解説 ： ①「各分野の得点の最小値のうち、最も小さい分野は「科学」である。」より、Cのグラフが科学だとわかる。 →選択肢ウとオは解答として不適当。
②「「音楽」の中央値は50点である。」より、音楽のグラフはAかBのどちらかだとわかる。
④四分位範囲は第1四分位数から第3四分位数までの範囲(箱の左端から右端まで)である。「「スポーツ」と「歴史」の四分位範囲は等しい。」より、スポーツと歴史の組み合わせは、AとDか、CとEとわかる。ただし、①の文章から、Cは科学とわかっているので、スポーツと歴史はAとDだとわかる。 →エとクの選択肢は不適当。
②と④を組み合わせて考えると、④よりAはスポーツか歴史になるので、音楽はBとわかる。 →キ、クの選択肢は不適当。
ここまでで、A：スポーツ or 歴史、B：音楽、C：科学、D：スポーツ or 歴史、E：文化 と判明する。
③「「文化」の第1四分位数は、「スポーツ」の第1四分位数より大きい。」を検討すると、E：文化より第1四分位数が小さい方がスポーツなので、Aがスポーツだとわかる。よって、Dは歴史だといえる。
したがって、B：音楽 D：歴史の選択肢のアが正解となる。
問題２－２ ：
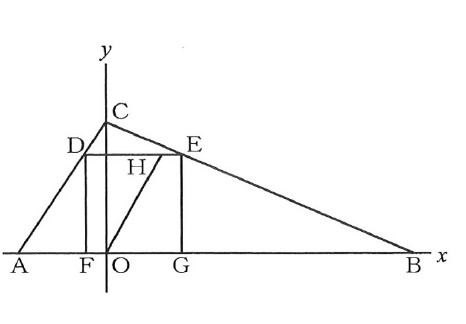
図で、Oは原点、A、B、Cは平面上の点であり、座標はそれぞれ(-2, 0)、(7, 0)、(0, 3)である。また、D、Eはそれぞれ線分CA、線分CB上の点、F、Gはそれぞれx軸上の点で、四角形DFGEは正方形であり、Hは線分DE上の点である。
四角形DFOHと四角形HOGEの面積が等しいとき、点Hのx座標として正しいものを、次のアからオまでの中から一つ選びなさい。
ア x=9/8 イ x=6/5 ウ x=11/9 エ x=5/4 オ x=7/4
解答 ： エ 5/4
解説 ：まず、直線ACと直線BCの式を求める。
直線ACはA(-2, 0)とC(0, 3)より、傾きが3/2とわかり、切片が₊3なので、y=3/2x+3となる。
直線BCはB(7, 0)とC(0, 3)を通るので、傾きが-3/7、切片は₊3となり、y=-3/7x+3
次に、問題文より四角形DFGEは正方形なので、この1辺をtとおく(DF=DE=EG=FG=t)。
よって、点Dのy座標はtとなり、これを直線ACの式に代入して、t=3/2x+3 →3/2x=t-3 →x=(2t-6)/3 したがって、点Dの座標は( (2t-6)/3, t)となる。
同様に点Eのy座標もtであり、直線BCの式に代入すると、t=-3/7x+3 →3/7x=-t+3 →x=(-7t+21)/3 となり、点Eの座標は( (-7t+21)/3, t)とわかる。
ここで、前述のように四角形DFGEは正方形なので、DEの長さは他の辺と同様にtである。
よって、(点Eのx座標)-(点Dのx座標)もtとなる。
(-7t+21)/3 – (2t-6)/3=t →(-7t+21) – (2t-6)=3t (両辺を3倍) →-7t+21-2t+6=3t →12t=27 →t=27/12 →t=9/4
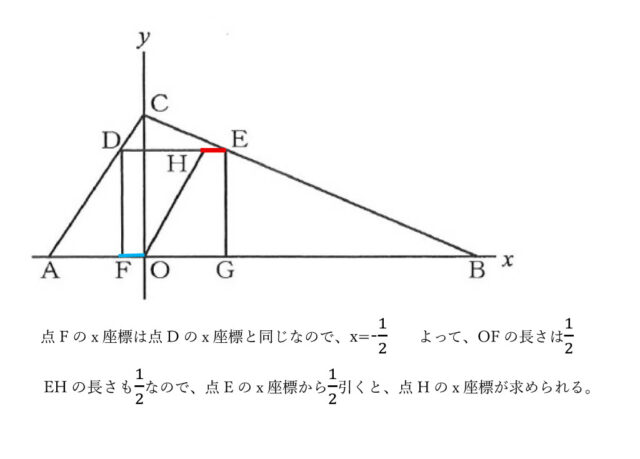
t=9/4を先に出した点Dのx座標に代入すると、x=(2×9/4-6)/3 →x=(18/4-6)/3 →x=-3/2×1/3 →x=-1/2 よって、点Dのx座標は-1/2
同様に点Eのx座標も、x=(-7×9/4+21)/3 →x=(-63/4+21)/3 →x=21/4×1/3 →x=7/4 よって、点Eのx座標は7/4
四角形DFOHと四角形HOGEの面積が等しいとき、それぞれの四角形は合同な台形になり、辺FOと辺EHの長さは等しくなる。先に求めた点Dのx座標より、辺OFの長さは1/2である。辺EHも同じ長さなので、先に求めた点Eのx座標を使って、7/4-1/2=5/4。以上より、点Hのx座標はx=5/4とわかる。
問題２－３ ➀：
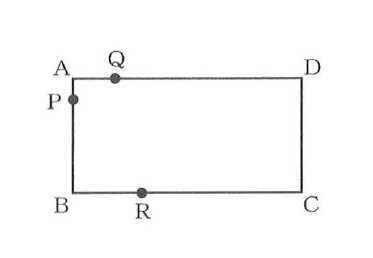
図で、四角形ABCDはAB=8cm、AD= l6cmの長方形である。点P、Qは頂点Aを同時に出発し、点Pは毎秒1cmの速さで辺AB上を頂点Bまで、点Qは毎秒2cmの速さで辺AD上を頂点Dまで移動する。また、点Rは点P、Qが頂点Aを出発したのと同時に頂点Cを出発し、毎秒8cmの速さで四角形ABCDの辺上を頂点B、A、D、Cの順に通って頂点Bまで移動する。点P、Qが頂点Aを出発してからx秒後の△APQの面積をycm²とするとき、次の①、②の問いに答えなさい。
なお、下の図を必要に応じて使ってもよい。
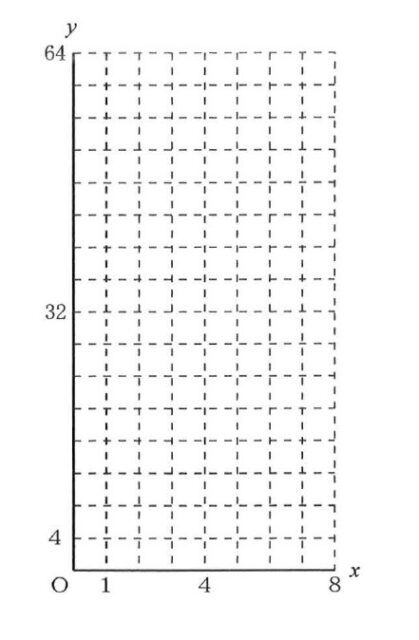
x=3のときのyの値として正しいものを、次のアからオまでの中から一つ選びなさい。
ア y=4 イ y=9 ウ y=12 エ y=18 オ y=25
解答 ： エ 5/4
解説 ： 点Pは、点Aを出発して毎秒1cmずつ点Bに向かって移動するので、APの長さは移動時間と等しくなる。よって、3秒後にはAP=3cmとなっている。同様に点Qは、点Ａを出発して点Ｄまで毎秒2cmで移動するので、3秒後にはAQ=6cmとわかる。
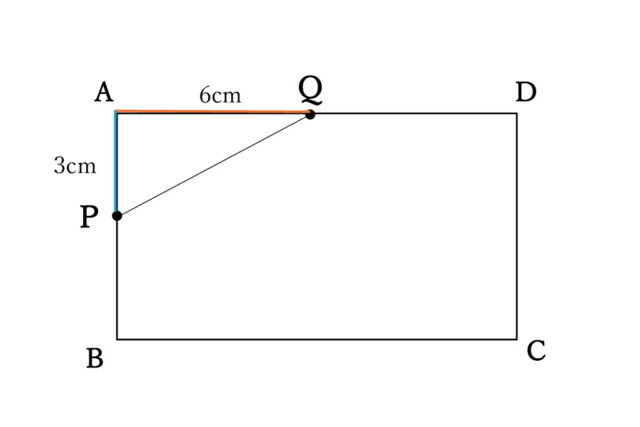
△APQの面積は、AP×AQ÷2で求められるので、先に求めたAP=3cmとAQ=6cmを代入すると、y=3×6÷2 →y=9
以上より、イが正解とわかる。
問題２－３ ➁：
3点P、Q、Rが同時に出発してから8秒後までの間で、△APQの面積と△ABRの面積が等しくなるときが何回かある。3回目に等しくなるときは何秒後から何秒後までの間にあるか、正しいものを次のアから力までの中から一つ選びなさい。
ただし、点Rが辺AB上にあるとき、△ABRの面積は0とする。
ア 2秒後から3秒後までの間 イ 3秒後から4秒後までの間
ウ 4秒後から5秒後までの間 エ 5秒後から6秒後までの間
オ 6秒後から7秒後までの間 カ 7秒後から8秒後までの間
解答 ：オ 6秒後から7秒後までの間
解説 ：まず△APQの面積に着目する。
点Pは毎秒1cmのスピードなので、頂点Aを出発してからx秒後のAPの長さはxcmといえる。同様に、点Qは毎秒2cmなので、頂点Aを出発してからx秒後のAQの長さは2xcmといえる。よって、x秒後の△APQの面積は、x×2x÷2=x² したがって、△APQの面積の式は、y=x²とわかる。
次に△ABRの面積について考える。
0秒のとき、BR=16cm、AB=8cmなので、16×8÷2=64cm²。1秒後は、BR=8cm、AB=8cmより、8×8÷2=32cm²。2秒後、3秒後は点Rが辺AB上にあるので、問題文より△ABRの面積は0。4秒後は、AR=8cm、AB=8cmなので、8×8÷2=32cm²。5秒後、6秒後はいずれも点Rが辺DC上にあるため、AR=16cm、AB=8cmより、16×8÷2=64cm²。7秒後はBR=8cm、AB=8cmより8×8÷2=32cm²。8秒後は点Rが点Bに到着するので辺AB上にあり、面積は0。
以上より、1~8秒までの△APQと△ABRの面積の変化を表にまとめることができる。
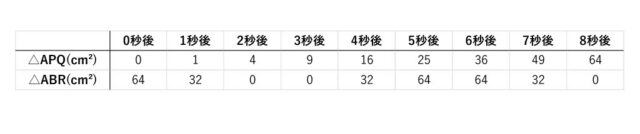
この表の値からグラフを作ると、以下のようになる。
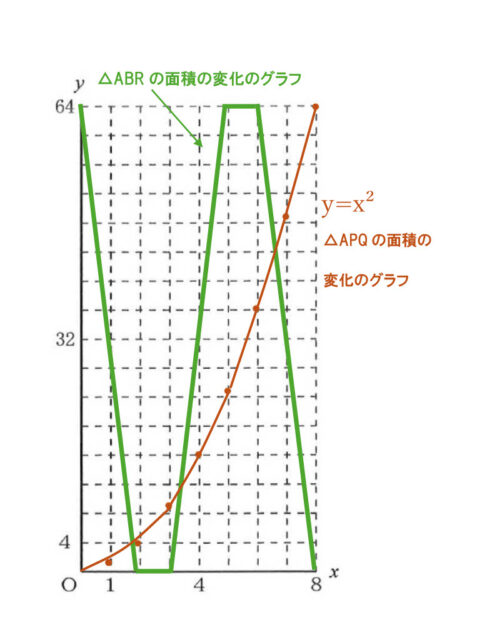
以上より、△APQの面積と△ABRの面積が3回目に等しくなるときは、6秒後から7秒後までの間だとわかる。よって、オが適当。
問題３-１：
図で、C、Dは線分ABを直径とする円0の周上の点で、CB =CDである。∠COA= 48°のとき、∠OBDの大きさは ∠アイ 度である。
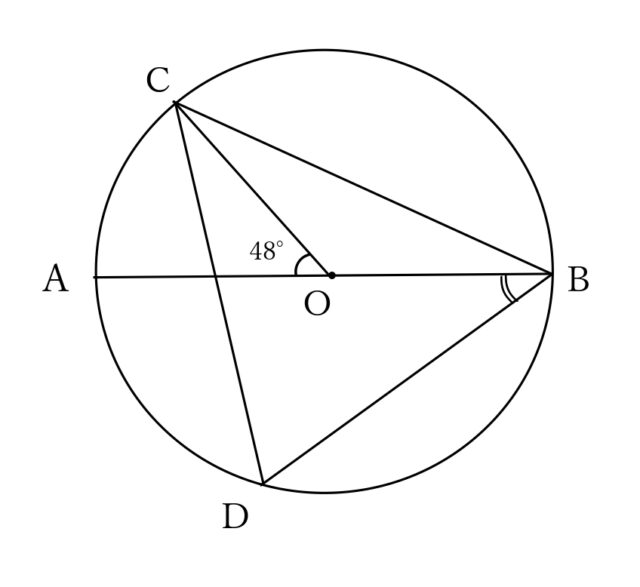
解答 ：42 度
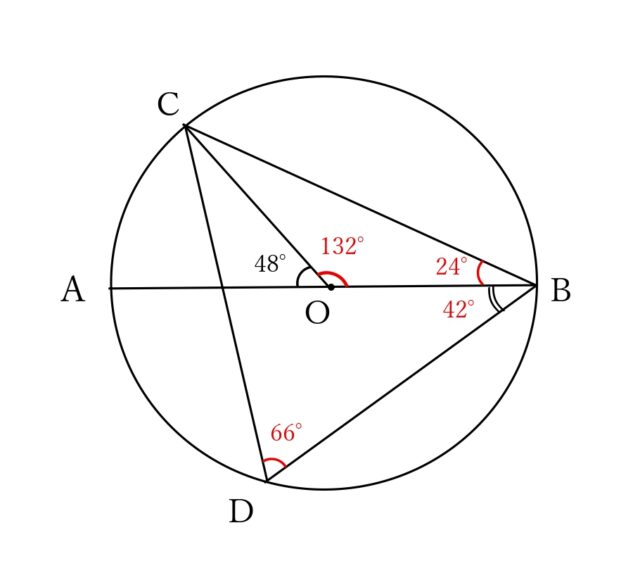
解説 ：直線は180°なので、∠COB=180°-∠COA=180°-48°=132° よって、∠COB=132°。
円周角の定理より、同じ弧からなる円周角は中心角の半分なので、
∠CDB=∠COB÷2=132°÷2=66° したがって、∠CDB=66°。
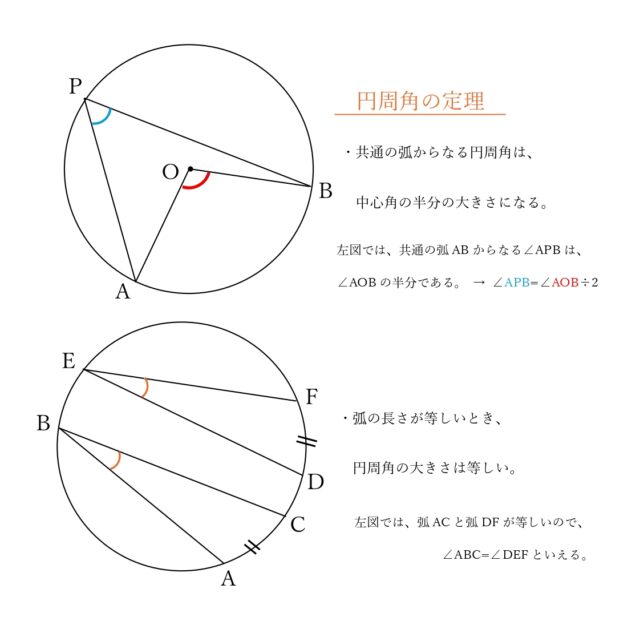
同様に、∠CBA=∠COA÷2=48°÷2=24°
問題文より、CB=CDなので、弧CB=弧CDといえる。
同じ長さの弧からなる円周角の大きさは等しいので、∠CDB=∠CBD=66°。
∠CBA+∠ABD=66°なので、24°+∠ABD=66° ∠ABD=66°-24°=42°。よって、∠OBD=42°
問題３-２ ➀：
図で、四角形ABCDは長方形、Eは辺AD上の点で、AE:ED=2:1 、Fは辺DC上の点で、DB⊥EFである。また、Gは線分DBとEFの交点である。
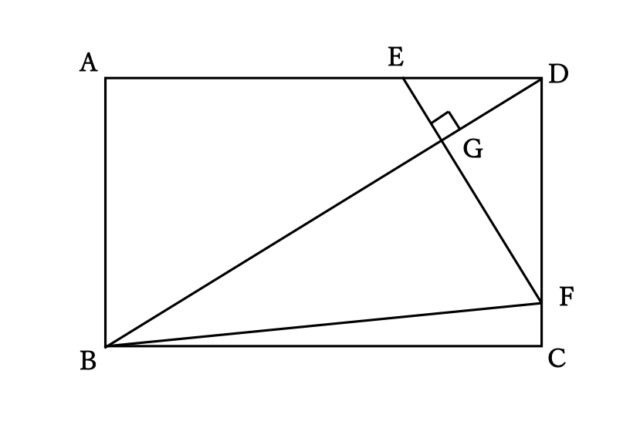
AB=4cm、AD=6cmのとき、
線分DGの長さは線分DBの長さの ア/イウ 倍である。
解答 ：3/13 倍
解説 ：△BADと△EGDについて、共通なので∠BDA=∠EDG…①
∠EGD=90°なので、∠BED=∠EDG=90°…②
∠ABD=180°-∠BAD-∠BDA=180°-90°-∠BDA=90°-∠BDA…③
∠GED=180°-∠EGD-∠EDG=180°-90°-∠EDG=90°-∠EDG…④
①、③、④より、∠ABD=∠GED…⑤
①、⑤より、2組の角がそれぞれ等しいので、△BAD∽△EGD
△BADについて、三平方の定理を使ってBD²=BA²+AD² →BD²=4²+6²=16+36=52° →BD=±2√13 BD＞0なので、BD=2√13
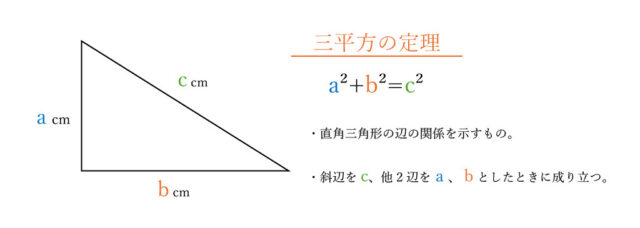
△BAD∽△EGDなので、DA:DG=BD:ED →6:DG=2√13:2 →2√13×DG=6×2 →DG=12/2√13=(12×√13) / 2√13×√13=12√13 / 2×13=6√13/13 よって、DG=6√13/13
したがって、DG/DB=DG÷DB=6√13/13÷2√13=3/13 以上より、3/13倍
問題３-２ ➁：
△GBFの面積は エオ/カキ cm²である。
解答 ：90/13 cm²
解説 ：△DGFと△EGDについて、まずは△DGFに着目する。
∠EDF=90°なので、∠EDF=∠EDG+∠GDF=90°となる。ここから、∠GDF=90°-∠EDGといえる。…①
次に△EGDを見ると、三角形の内角の和は180°なので、∠GED+∠EGD+∠EGD=180°である。よって、∠GED=180°-∠EGD-∠EGD →∠GED=180°-90°-∠EGD →∠GED=90°-∠EGDとなる。…②
①、②より、∠GDF=90°-∠EDG=∠GED…③
また、∠EGD=∠DGF=90°…④
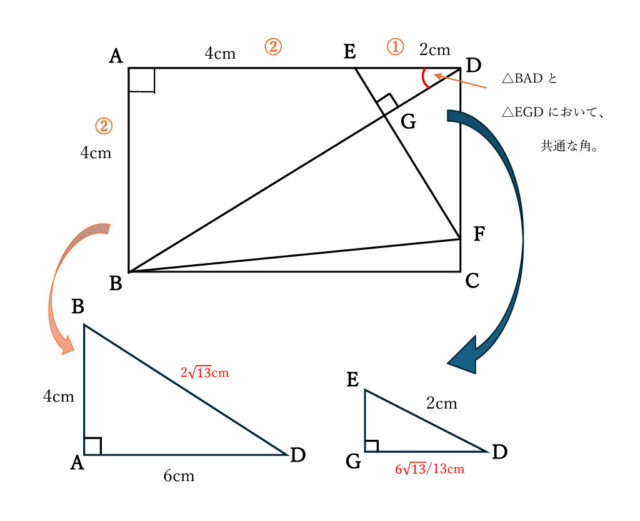
③、④より、2組の角がそれぞれ等しいので、△DGF∽△EGDとなる。
加えて、(1)より△BAD∽△EGDなので、△BAD∽△DGFといえる。
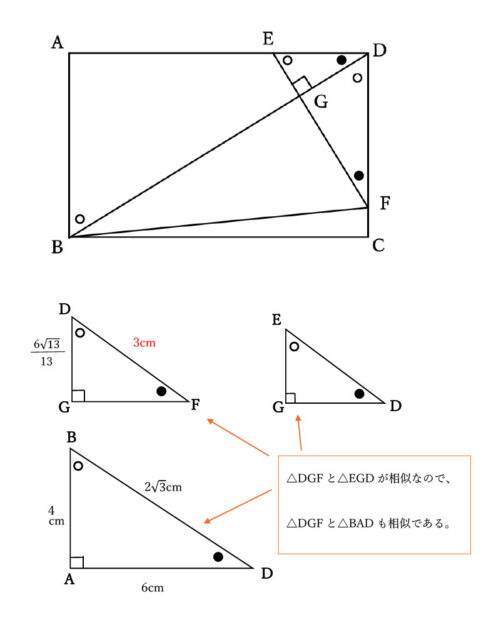
相似な図形において、対応する辺の比は等しいので、BA:BD=DG:DF。
(1)より、BD=2√13なので、4:2√13=6√13/13:DF →4DF=2√13×6√13/13 →4DF=12 →DF=3
また、DC=4cmなので、FC=1cmとわかる。
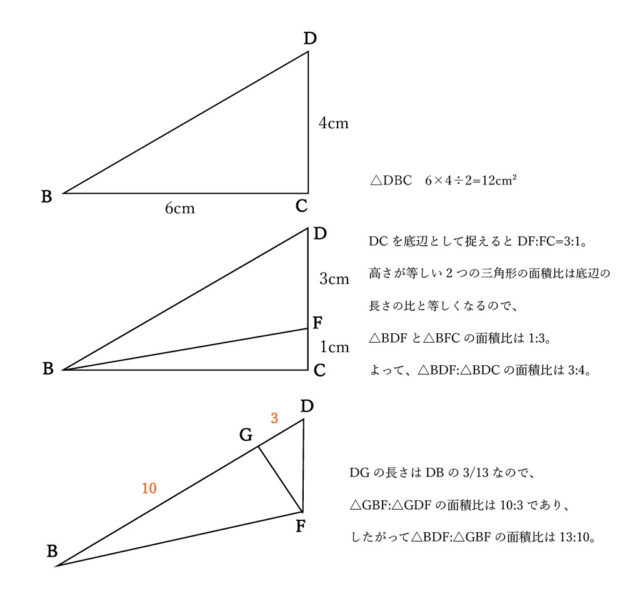
△BDCの面積は6×4÷2=12
△DBCについてDCを底辺として捉えるとDF:FC=3:1である。高さが等しい2つの三角形の面積比は底辺の長さの比と等しくなるので、△BDFと△BFCの面積比は1:3、△BDF:△BDC=3:4とわかる。よって、△BDF=△BDC×3/4 →△BDF=12×3/4 →△BDF=9
同様に、△GBFと△GDFも高さが共通で底辺の長さの比が面積の比になるため、(1)で求めたDGの長さはDBの3/13ということから、△GBF:△GDF=10:3であり、且つ△BDF:△GBF=13:10とわかる。
よって、△GBF=△GDF×10/13 →△GBF=9×10/13 →△GBF=90/13 以上より、答えは90/13とわかる。
問題３-３ ➀：
図で、立体OABCDは、正方形ABCDを底面とする正四角すいである。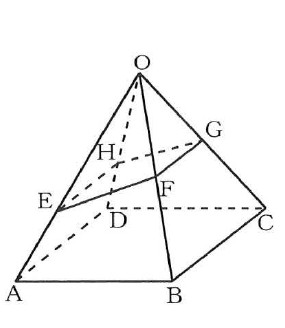
また、E、F、G、Hはそれぞれ辺OA、OB、OC、OD上の点で、OE:EA=2:1、OF:FB=1:1であり、CB//GF、DA//HEである。
OA=12 cm、AB=6cmのとき、
△OBDの面積は アイ√ウ cm²である。
解答 ：18√7 cm²
解説 ：DBの長さは△DABで三平方の定理を使って求めることができる。
立体CABCDは正四角すいなので、DA=AB=6cmであり、DB²=DA²+AB²なので、
DB²=6²+6² →DB²=72 →DB=±6√2 DB＞0より、DB=6√2。
次に△OBDの高さを求めたい。点OからDBに垂直におろした線とDBとの交点をPとおく。すると、DPはDBの半分なので、DP=3√2とわかる。
また、△ODPにおいて、三平方の定理よりOP²+DP²=OD²といえる。よって、OP²+(3√2)²=12² →OP²=144-18 →OP²=126 →OP=±3√14 OP＞0なので、OP=3√14とわかる。
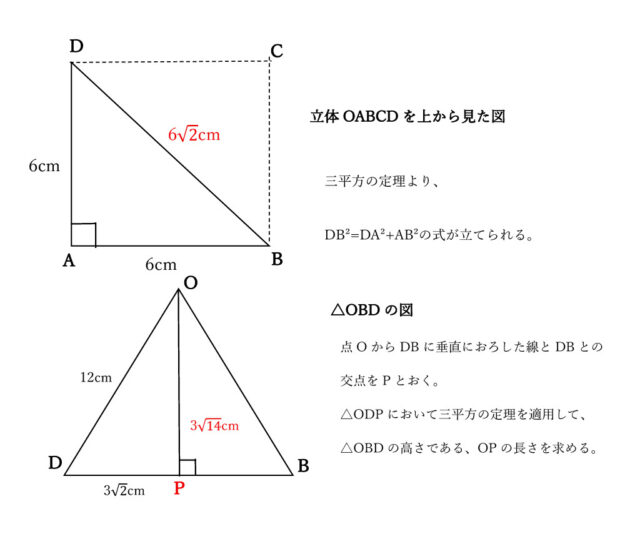
以上より、△OBDの面積はDB×OP÷2で求められるので、6√2×3√14÷2=9√28=18√7
したがって、答えは18√7となる。
問題３-３ ➁：
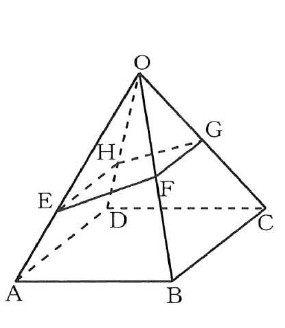立体OEFGHの体積は エ√オカ cm³である。
解答 ：7√14 cm³
解説 ：立体OEFGHを、△OBDで左右に分断して考える。
まず左半分に着目する。
立体OABDは、底面が△DAB、高さは①で求めた3√14である。よって体積は、6×6÷2×3√14÷3=18√14とわかる。
ちじみ率を使って、左半分の立体OHEFは、18√14×2/3×2/3×1/3=4√14と計算できる。
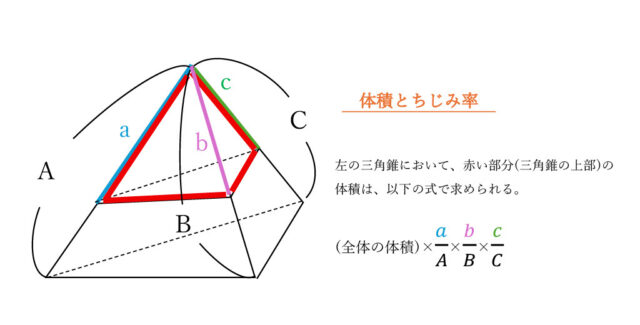
同様に右半分の立体OBCDは、18√14×1/2×1/2×2/3=3√14となる。
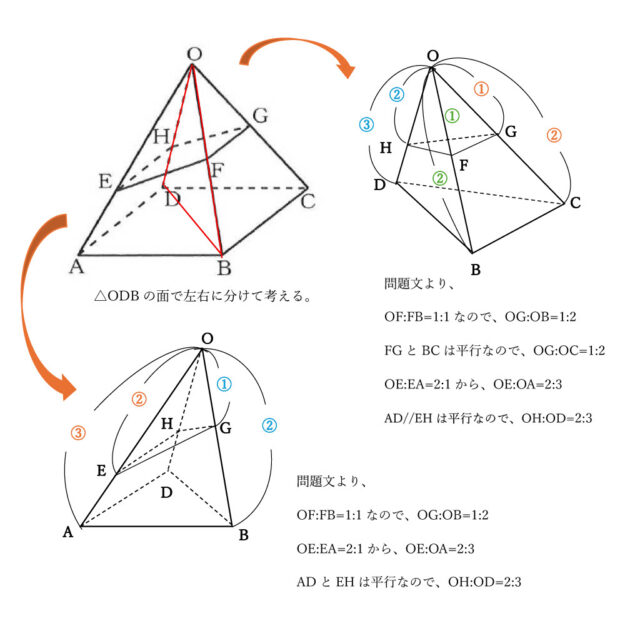
立体OEFGHの体積は、先に求めた2つの立体を足した体積なので、4√14+3√14=7√14。
以上より、立体OEFGHの体積は7√14cm³とわかる。
