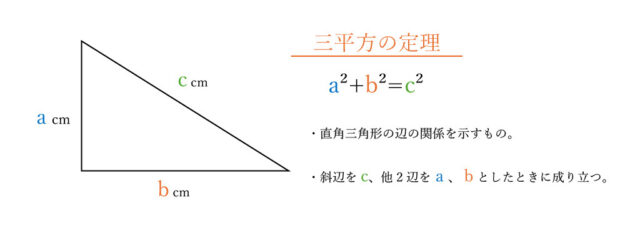
■問題PDF
令和7年度_学力検査問題過去問【東京】- 数学
■目次
大問1
大問2
大問3
大問4
大問5
■大問1
次の各問に答えよ。
(問1)3-6²÷4 を計算せよ。
解答 : -6
解説 : ・足し算や引き算より、掛け算割り算を優先的に計算する。
3-6²÷4=3-36÷4=3-9=-6 よって、答えは -6。
(問2)(9a-b)/5-a+2b を計算せよ。
解答 : (4a+9b)/5 (4a/5+9b/5)
解説 :(9a-b)/5-a+2b=9a/5-b/5-a+2b=9a/5-a-b/5+2b=9a/5-5a/5-b/5+10b/5=(9a-5a)/5-(b-10b)/5=4a/5-(-9b)/5=4a/5+9b/5 よって、答えは 4a/5+9b/5。
(問3)(3√7+8)(3√7-8) を計算せよ。
解答 :-1
解説 :・乗法公式「x²-a²=(x-a)(x+a)」を使う。
(3√7+8)(3√7-8)=(3√7)²-8²=63-64=-1 よって、答えは-1。
(問4)一次方程式 (9x-6)/2=4x+1 を解け。
解答 : 8
解説 : ・まずは、左辺の分数をなくす(分母をなくす)ために、両辺に2をかける。その後、移行して左辺にx、右辺に整数をまとめて方程式を解く。
(9x-6)/2=4x+1 →9x-6=(4x+1)×2 →9x-6=8x+2 →9x-8x=2+6 →x=8 よって、x=8
(問5)連立方程式 8x-5y=-3, y=2x-1 を解け。
解答 : x=4, y=7
解説 : ・1つの式が「y=~」のかたちになっているので、代入法で解く。
y=2x-1を8x-5y=-3に代入する。
8x-5(2x-1)=-3 →8x-10x+5=-3 →-2x=-3-5 →-2x=-8 →2x=8 →x=4
x=4をy=2x-1に代入して、y=2×4-1=8-1=7 よって、x=4, y=7
※式を変形すれば、加減法でも解くことができる。
(問6)二次方程式 x²-9x+7=0 を解け。
解答 : (9±√53)/2
解説 : 因数分解できないので、解の公式を使って解く。

x=(9±√9²-4×1×7)/2×1 →x=(9±√81-28)/2 →x=(9±√53)/2 よって、答えはx=(9±√53)/2
(問7)次の[ ① ]と[ ② ]に当てはまる数を,下のア~クのうちからそれぞれ選び,記号で答えよ。
関数y=-x²について,x の変域が-2≦x≦3のときのyの変域は,[ ① ]≦y≦[ ② ]である。
ア -9 イ -6 ウ -4 エ -2 オ 0 カ 4 キ 6 ク 9
解答 :① ア ② オ
解説 :y=-x²のグラフは次のようになる。
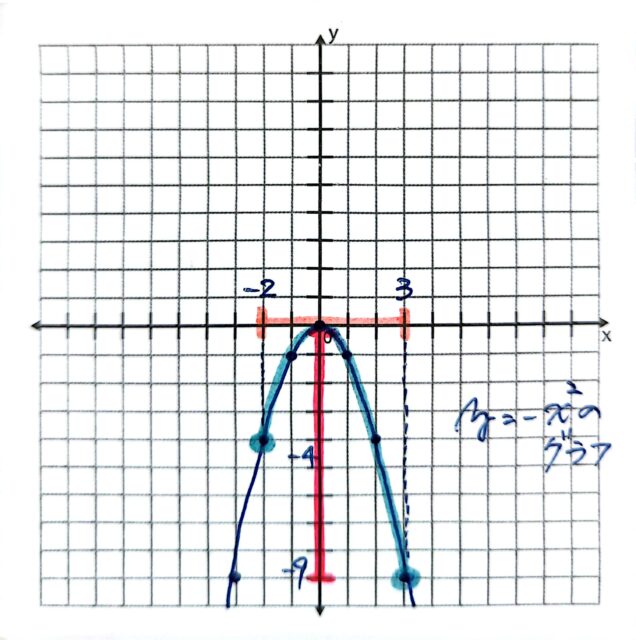
xの変域は、x軸(横軸)のピンクの範囲、y=-x²のグラフにおける-2≦x≦3の範囲は水色の部分、y=-x²のグラフの-2≦x≦3の範囲におけるyの変域が、y軸(縦軸)の赤の部分である。
-2≦x≦3の範囲のうち、最小値が①、最大値が②に入る。
yの値は縦軸で、上に行くほど値が大きく、下に行くほど値が小さくなる。よって、yの最大値は0、最小値は-9であるとわかる。よって、①はアの-9、②はオの0となる。
(問8)次の中の「あ」「い」に当てはまる数字をそれぞれ答えよ。
右の図1のように,1,2,3,4,5 の数字を1つずつ書いた5枚のカードがある。この5枚のカードから同時に3枚のカードをこの5枚のカードから同時に3枚のカードを取り出すとき,取り出した3枚のカードに書いてある数の和が10以上になる確率は,[ あ ]/[ い ]である。
ただし,どのカードが取り出されることも同様に確からしいものとする。
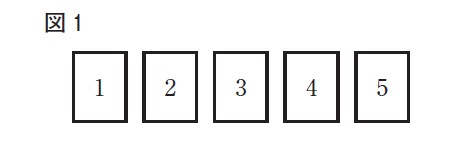
解答 : あ 2 い 5
解説 :樹形図を描いて考える。
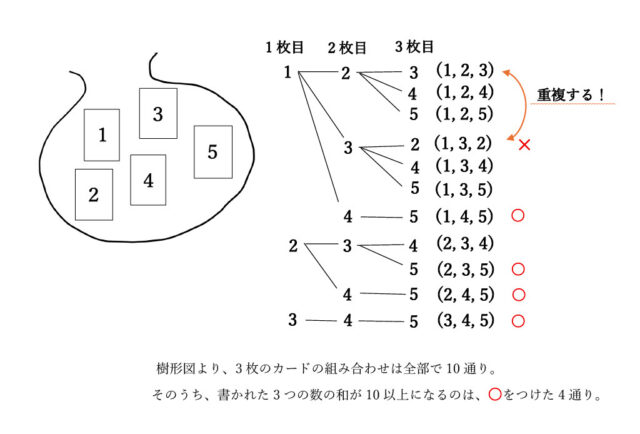
樹形図をみると、5枚から3枚取り出す組み合わせは、全部で10通りとわかる。また、取り出した3枚のカードに書かれた数の和が10以上になる組み合わせは、(1, 4, 5)、(2, 3, 5)、(2, 4, 5)、(3, 4, 5)の4通りである。よって、取り出した3枚のカードに書いてある数の和が10以上になる確率は4/10となり、2/5である。
以上より、[ あ ]に2、[ い ]には5が入る。
(問9)右の図2で,四角形ABCDは平行四辺形である。解答欄に示した図をもとにして,辺AD上にあり,頂点B,頂点Cまでの距離が等しい点Pを,定規とコンパスを用いて作図によって求め,点Pの位置を示す文字Pも書け。ただし,作図に用いた線は消さないでおくこと。
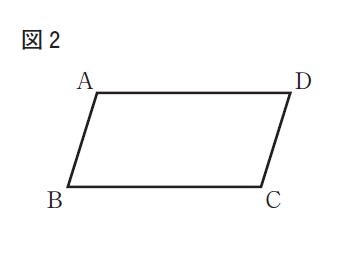
解答 :
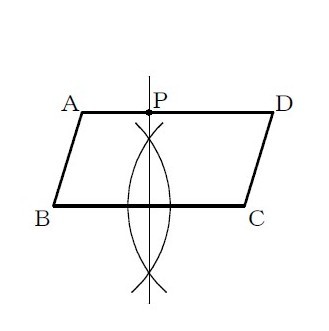
解説 :点Pについて、頂点B,頂点Cまでの距離が等しいということから、点Pは辺BCの垂直二等分線上にある点だとわかる。
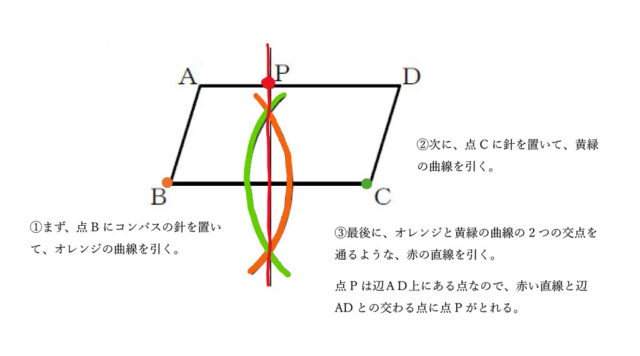 よって、垂直二等分線と辺ADとの交点をとって、点Pと記す。
よって、垂直二等分線と辺ADとの交点をとって、点Pと記す。
■大問2
(問1)Sさんのクラスでは,先生が示した問題をみんなで考えた。
次の各問に答えよ。
[先生が示した問題]
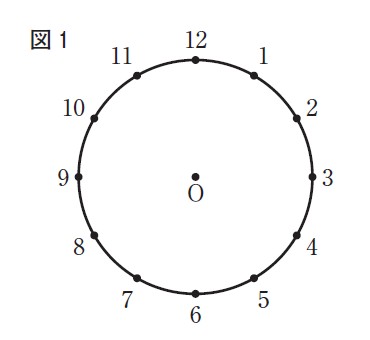
右の図1のように,円Oの円周を12等分する点に,1から12までの自然数の番号を,小さい順で時計回りに付ける。
1から12までの番号を付けた点のうち,2点を結んでできる線分が円Oの直径となるとき,その2点を向かい合う点とする。
例えば,1の点と7の点は,向かい合う点である。
図1において,1組の向かい合う点を選び,それぞれの点の番号のうち,小さい方の数をa,大きい方の数をbとする。
a,bの平均値をA,b²- a²の値をBとするとき,BはAの何倍か求めなさい。
[先生が示した問題]で,BはAの[ ]倍と表すとき, [ ]に当てはまる数を,次のア〜エのうちから選び,記号で答えよ。
ア 3 イ 4 ウ 6 エ 12
解答 : エ
解説 : [先生が示した問題]の中で例として書かれている、1の点と7の点を使って考える。
そのうち、小さい方の数をa、大きい方の数をbとするので、この場合、a=1、b=7である。
Aはa、bの平均値なので、(1+7)÷2=8÷2=4 よって、A=4。次にBはb²- a²の値なので、7²-1²=49-1=48 したがって、B=48。BがAの何倍かを求めるので、48÷4=12。よって、12倍とわかる。
(2, 8)について。A=(2+8)÷2=5 B=8²-2²=64-4=60 B÷A=60÷5=12
(3, 9)について。A=(3+9)÷2=6 B=9²-3²=81-9=72 B÷A=72÷6=12
(6, 12)について。A=(6+12)÷2=9 B=12²-6²=144-36=108 B÷A=108÷9=12
以上のように、向かい合う他の点の組み合わせでもBはAの12倍になる。
よって、選択肢エの12が適当である。
(問2)Sさんのグループは,[先生が示した問題]をもとにして,次の問題を作った。
[Sさんのグループが作った問題]
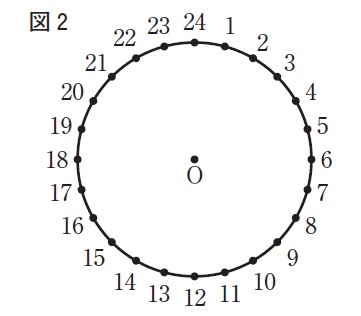
右の図2のように,円Oの円周を24等分する点に,1から24までの自然数の番号を,小さい順で時計回りに付ける。1から24までの番号を付けた点のうち, 2点を結んでできる線分が円Oの直径となるとき,その2点を向かい合う点とする。図2において,異なる2組の向かい合う点を選び,1組目のそれぞれの点の番号のうち,小さい方の数をa,大きい方の数をbとし,2組目のそれぞれの点の番号のうち,小さい方の数をc,大きい方の数をdとする。a,b,c,d の平均値をP,bd – ac の値をQとするとき,Q=24Pとなることを確かめてみよう。
[Sさんのグループが作った問題]で,Q=24Pとなることを証明せよ。
解答 : [証明]
bをaを用いて表すと、bはaより12大きい数なので、b=a+12。同様に、dもcより12大きいので、d=c+12と表せる。
まず、Pはa、b、c、d の平均値なので、{a+(a+12)+c+(c+12)}÷4=(2a+12+2c+12)÷4=(2a+2c+24)/4=(a+c+12)/2 となる。よって、P=(2a+2c+24)/4。
次に24Pは、(2a+2c+24)/4×24なので、(2a+2c+24)×6=12a+12c+144 となり、24P=12a+12c+144。…①
また、Qはbd-acなので、(a+12)×(c+12)-ac=ac+12a+12c+144-ac=12a+12c+144 となり、Q=12a+12c+144 である。…②
①、②より、Q=12a+12c+144=24P となる。よって、Q=24Pである。[証明終]
解説 :
・数字がa、b、c、dと多いので、cをaを使って、dをcを使って表し、aとcの2種類の文字で表すところがポイントになっている。 例えば2の点に向かい合う点は14、10の点に向かい合う点は22なので、どちらも小さい数字に12を足すと、向き合う大きい点の数になることがわかる。
[証明]
bをaを用いて表すと、bはaより12大きい数なので、b=a+12。同様に、dもcより12大きいので、d=c+12と表せる。
まず、Pはa、b、c、d の平均値なので、{a+(a+12)+c+(c+12)}÷4=(2a+12+2c+12)÷4=(2a+2c+24)/4=(a+c+12)/2 となる。
よって、P=(2a+2c+24)/4。
次に24Pは、(2a+2c+24)/4×24なので、(2a+2c+24)×6=12a+12c+144 となり、24P=12a+12c+144。…①
また、Qはbd-acなので、(a+12)×(c+12)-ac=ac+12a+12c+144-ac=12a+12c+144 となり、Q=12a+12c+144 である。…②
①、②より、Q=12a+12c+144=24P となる。よって、Q=24Pである。[証明終]
■大問3
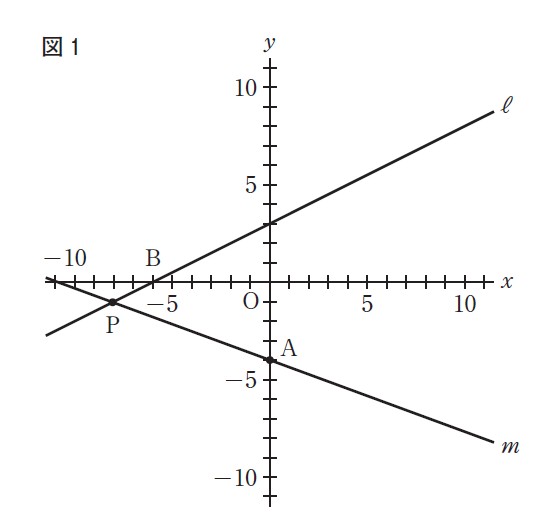
(問1)右の図1で,点Oは原点,点Aの座標は(0, -4)であり、直線ℓは一次関数y=1/2x+3のグラフを表している。
直線ℓとx軸との交点をBとする。直線ℓ上にある点をPとし,2点A,Pを通る直線をmとする。
次の各問に答えよ。
点Pのy座標が-1のとき,点Pのx座標を,次のア〜エのうちから選び,記号で答えよ。
ア -8 イ -9/2 ウ -2 エ 5/2
解答 :ウ
解説 : 点Bの座標は、グラフより(-6, 0)と読み取れる。
この点が点Pと一致するということは、点Pは直線ℓ上にあって、且つ直線mも通る点なので、直線mは(-6, 0)を通ることがわかる。
直線mは、グラフより切片が-4と読み取れるので、ここから y=ax-4 とおくことができる。またこの直線は、(-6, 0)を通るので代入して、0=a×(-6)-4 →0=-6a-4 →6a=-4 →6a×1/6=-4×1/6 →a=-4/6 →a=-2/3 よって、直線mの傾きは-2/3となる。
以上より、直線mの式は、y=-2/3x-4 となる。よって、選択肢ウが正しい。
(問2)点Pが点Bに一致するとき,直線mの式を,次のア〜エのうちから選び,記号で答えよ。
ア y=-3/2x-4 イ y=-3/2-6 ウ y=-2/3x-4 エ y=-2/3x-6
解答 : ウ
解説 : 点Bの座標は、グラフより(-6, 0)と読み取れる。
この点が点Pと一致するということは、点Pは直線ℓ上にあって、且つ直線mも通る点なので、直線mは(-6, 0)を通ることがわかる。
直線mは、グラフより切片が-4と読み取れるので、ここから y=ax-4 とおくことができる。またこの直線は、(-6, 0)を通るので代入して、0=a×(-6)-4 →0=-6a-4 →6a=-4 →6a×1/6=-4×1/6 →a=-4/6 →a=-2/3 よって、直線mの傾きは-2/3となる。
以上より、直線mの式は、y=-2/3x-4 となる。よって、選択肢ウが正しい。
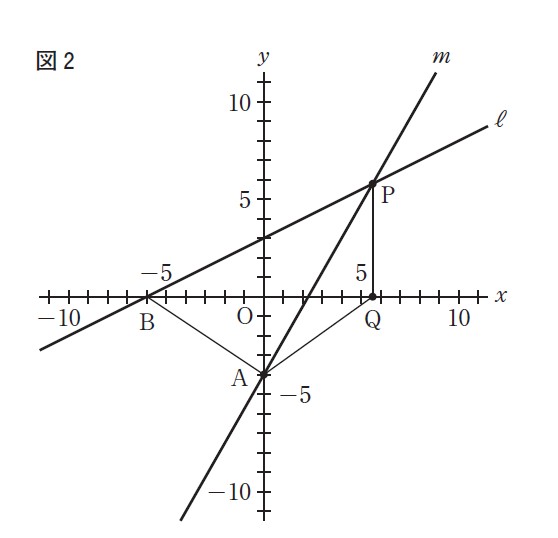
(問3)右の図2は,図1において,点Pのx座標が正の数のとき,x軸上にありx座標が点Pのx座標と等しい点をQとし,点Aと点B,点Aと点Q,点Pと点Qをそれぞれ結んだ場合を表している。
△APBの面積が△AQPの面積の2倍になるとき,点Pのx座標を求めよ。
解答 : 7
解説 : まず、点Pのx座標をtとおく。
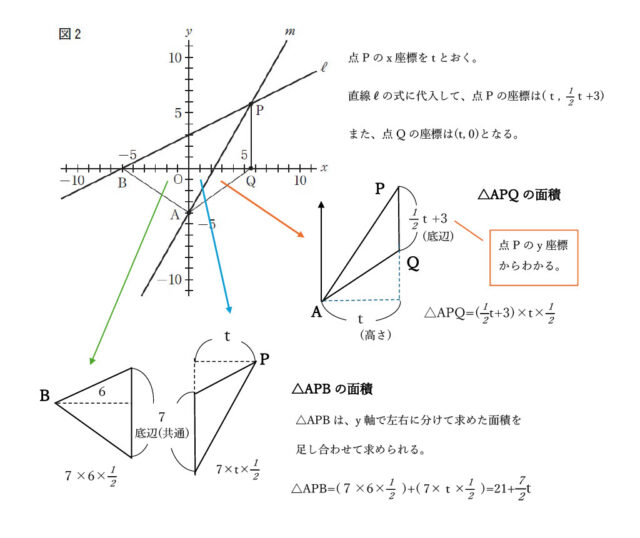
点Pは直線ℓ上の点なので、点Pのy座標は直線ℓに代入することで求められる。直線ℓの式であるy=1/2x+3にx=tを代入して、y=1/2t+3 となり、点Pの座標は(t, 1/2t+3)とわかる。
次に△APBの面積は、y軸の部分で左右に分けた面積を足し合わせることで求められる。
△APB=(7×6×1/2)+(7×t×1/2)=21+7/2t
△AQPの面積は、PQを底辺として、PQからy軸までの長さを高さとして求められる。
△AQP=(1/2t+3)×t×1/2=1/4t²+3/2t
問題文より、△APBの面積は△AQPの面積の2倍になるので、△APB=△AQP×2 という関係の式を作ることができる。
よって、△APB=△AQP×2 →21+7/2t=(1/4t²+3/2t)×2 →21+7/2t=1/2t²+3t →(21+7/2t)×2=(1/2t²+3t)×2 →42+7t=t²+6t →t²-t-42=0 →(t-7)(t+6)=0 →t=-6, 7 したがって、t=-6, 7
問題文より、点Pのx座標は正の数とあるので、t>0より、t=-6は不適。よって、t=7。
以上より、点Pのx座標は7とわかる。
■大問4
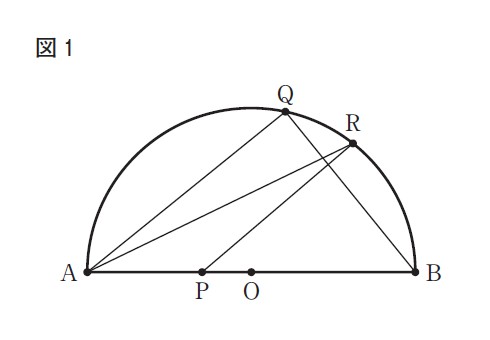
(問1)右の図1で,点Oは線分ABを直径とする半円の中心である。点Pは,線分OA上にある点で,点O,点Aのいずれにも一致しない。点Qは,弧AB上にある点で,点A,点Bのいずれにも一致しない。点Rは,弧BQ上にある点で,点B,点Qのいずれにも一致しない。点Aと点Q,点Aと点R,点Bと点Q,点Pと点Rをそれぞれ結ぶ。
次の各問に答えよ。
図1において,AQ=BQ,∠QAR=20°,∠ARP=a°とするとき,∠BPRの大きさを表す式を,次のア〜エのうちから選び,記号で答えよ。
ア (a+20)度 イ (a+25)度 ウ (155-a)度 エ (160-a)度
解答 : イ
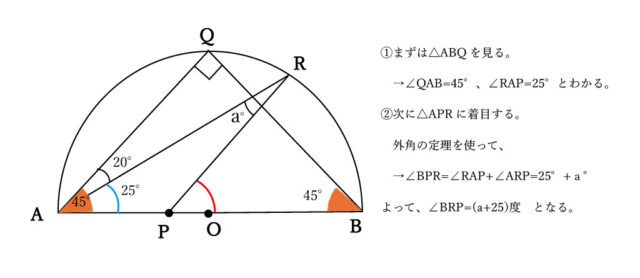
解説 : 問題文より、AQ=BQなので、△ABQは二等辺三角形であることがわかる。
円の定理より、半円を弧とする円周角は90°なので、∠AQB=90°とわかる。よって、∠AQB+∠QAB+∠QBA=180° →90°+∠QAB+∠QBA=180° →∠QAB+∠QBA=180°-90° →∠QAB+∠QBA=90° となる。また、△ABQは二等辺三角形なので、∠QAB=45°と求められる。また問題文より、∠QAR=20°なので、∠RAP=∠QAB-∠QAR=45°-20°=25° したがって、∠RAP=25°とわかる。
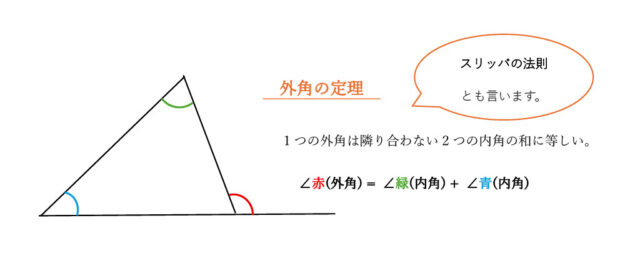
求めたい∠BPRは△APRの外角であり、「外角の定理」より三角形の1つの外角は隣り合わない2つの内角の和に等しいので、
∠BPR=∠RAP+∠ARP と表せる。問題文より∠ARP=a°であり、先に求めた∠RAP=25°とを使って、∠BPR=∠RAP+∠ARP=25°+a° よって、∠BPR=(a+25)度とわかる。したがって、選択肢イが正答。
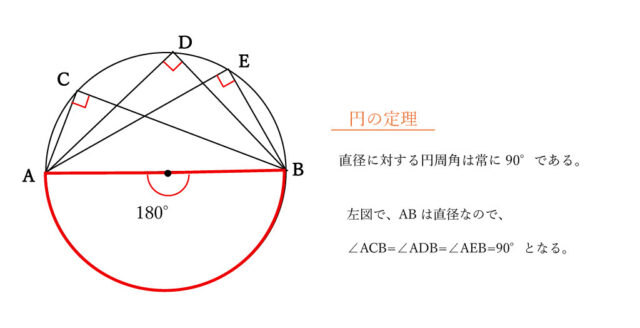
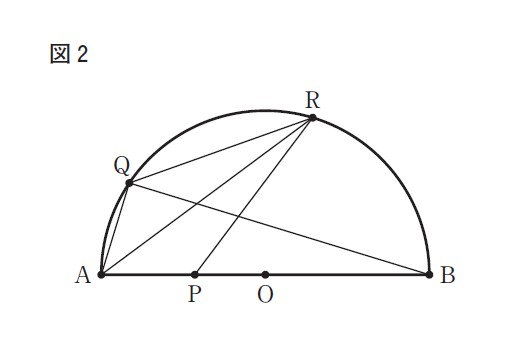
(問2)① 右の図2は,図1において,AP=AQ,弧BR=弧QRのとき,点Qと点Rを結んだ場合を表している。次の①,②に答えよ。
△APR≡△AQRであることを証明せよ。
解答 :
[証明]
△APRと△AQRについて、
共通な辺なので、 AR=AR …(a)
仮定より、 AP=AQ …(b)
同じく仮定から弧BR=弧QRであり、
等しい弧に対する円周角は等しいので、
∠PAR=∠QAR …(c)
(a)~(c)より、
2組の辺とその間の角がそれぞれ等しいので、
△APR ≡ △AQR である。 [証明終]
解説 :
[証明]
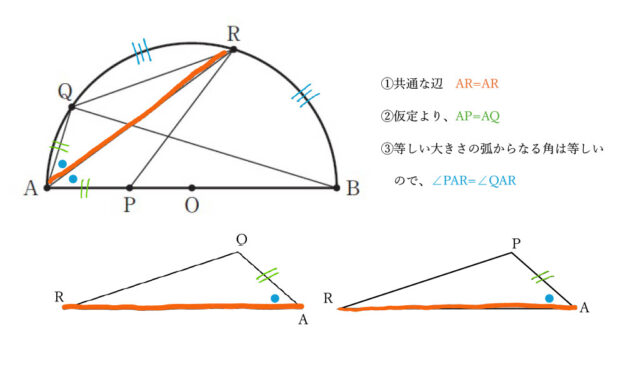
△APRと△AQRについて、
共通な辺なので、 AR=AR …(a)
仮定より、 AP=AQ …(b)
同じく仮定から弧BR=弧QRであり、
等しい弧に対する円周角は等しいので、
∠PAR=∠QAR …(c)
(a)~(c)より、
2組の辺とその間の角がそれぞれ等しいので、
△APR ≡ △AQR である。 [証明終]
(問2)② 次の[ ]の中の「う」「え」に当てはまる数字をそれぞれ答えよ。

図2において,線分ARと線分BQとの交点をS,点Oと点Rを結び,線分BQと線分ORとの交点をTとした場合を考える。
AP=2OPのとき,△RSTの面積は,四角形AORQの面積の[ う ] / [ え ]倍である。
解答 : う:1 え:5
解説 : まずは、問題文と図から分かることを整理する。
AP=2POなので、AP:PO=2:1 …(ⅰ)
△OARについて、辺OAと辺ORはどちらも円Oの半径なので、OA=ORとわかる。…(ⅱ)
(ⅱ)より、△OARは二等辺三角形であり、2つの底角は等しくなるので、∠OAR=∠ORA。…(ⅲ)
円周角の定理より、半径からなる円周角は90°なので、∠BQA=90°。…(ⅳ)
①で証明した△APR ≡ △AQRより、合同な三角形の対応する角は等しいので∠QAR=∠OARとわかる。(ⅲ)より∠OAR=∠ORAであることも踏まえると、∠QAR=∠OAR=∠ORAであり、∠QAR=∠ORAといえる。この2つの角は錯角であり、AQ//ROとわかる。
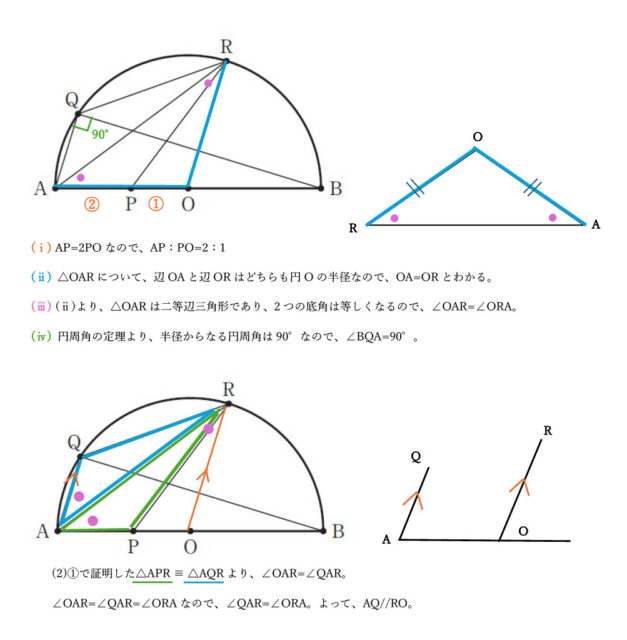
次に△BAQと△BOTについて、∠QBA=∠TBO…(a)
AQ//ROより同位角は等しいので、(d)も踏まえて、∠BQA=∠BTO…(b)
(a)(b)より、2組の角がそれぞれ等しいので、△BAQ∽△BOT
BOは円Oの半径、BAは直径なので、BO:BA=1:2
相似な三角形の対応する辺の比は等しいので、TO:QA=1:2
(ⅰ)(ⅱ)より、AP:PO=2:1で、且つOA=ORなので、RT:TO=2:1。
また、QA:RT=2:2=1:1とわかる。よって、QA=RTである。…(ⅴ)
△BAQ∽△BOTより、∠BQT=∠BTOである。また、対頂角は等しいので、∠BTO=∠STR。したがって、∠BQT=∠BTO=∠STRであり、∠SQA=∠STR。…(ⅵ)
△ASQと△RSTにおいて、(ⅴ)、(ⅵ)と∠QAS=∠TRSより、1組の辺とその両端の角が等しいので、△ASQ≡△RSTといえる。合同な三角形の対応する辺は等しいので、QS:ST=1:1、RS:SA=1:1とわかる。
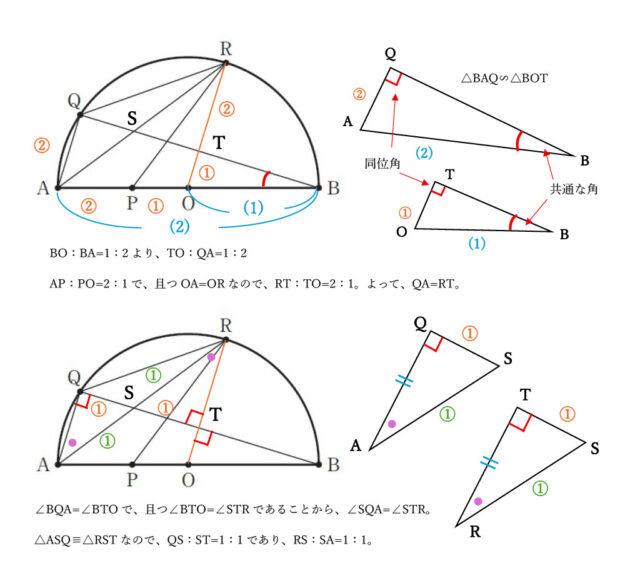
△RSTの面積をxとおく。
すると、△RQSは△RSTと底辺の比が等しく、高さも等しいので、△RQSの面積も同様にxである。また、△ASQ≡△RSTなので、△ASQの面積も同様にxと考えられる。加えて、△ATSと△RSQにおいて、SQ=ST、SR=SA、対頂角より∠QSR=∠TSAより、2組の辺とその間の角が等しいので、△ATS≡△RSQである。よって、△ATSの面積もxとわかる。
次に、△TAOと△RATに着目する。
この2つの三角形は高さは等しく、底辺のOTとTRの比はOT:TR=1:2なので、面積の比も1:2である。△RATは△RSTと△ATSの和なので、面積は2xであり、よって、△TAOの面積はxだと考えられる。
したがって、四角形AORQの中には面積がxの三角形の5つ分であり、これは四角形AORQの面積は△RSTの面積の5倍ということである。以上より、△RSTの面積は,四角形AORQの面積の1/5とわかる。よって、[ う ]は1、[ え ]は5が適当である。
■大問5
(1)右の図1に示した立体ABCD-EFGHは,AB=AD=6cm,AE=4cmの直方体である。頂点Aと頂点Cを結び,線分AC上にある点をPとする。頂点Hと点Pを結ぶ。
次の各問に答えよ。
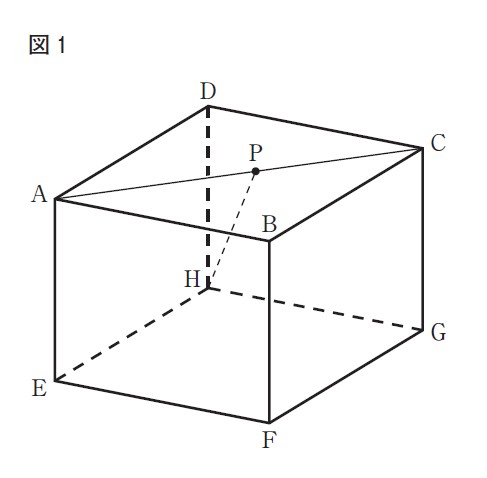
次の[ ]の中の「お」「か」に当てはまる数字をそれぞれ答えよ。
図1において,頂点Dと点P,頂点Eと点Pをそれぞれ結んだ場合を考える。
点Pが線分ACの中点のとき,立体P-AEHDの体積は,[ おか ]cm³である。
解答 : お:2 か:4
解説 :立体P-AEHDの底面を、面AEHDとして考える。
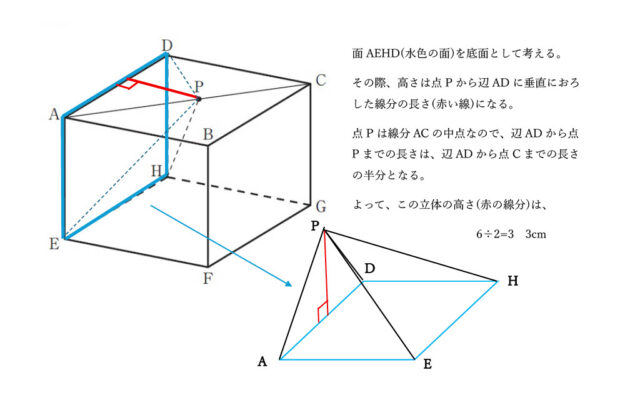
点Pは辺ACの中点なので、辺ADから点Pまでの高さは辺BAの長さの半分と等しくなる。よって、面AEHDを立体P-AEHDの底面として考えたとき、この立体の高さは6÷2=3 となり、3cmとわかる。
よって、立体P-AEHDの体積は、6×4×3×1/3=24
したがって、24cm³とわかり、[ お ]は2、[ か ]は4が正答である。
(2)次の[ ]の中の「き」「く」「け」に当てはまる数字をそれぞれ答えよ。
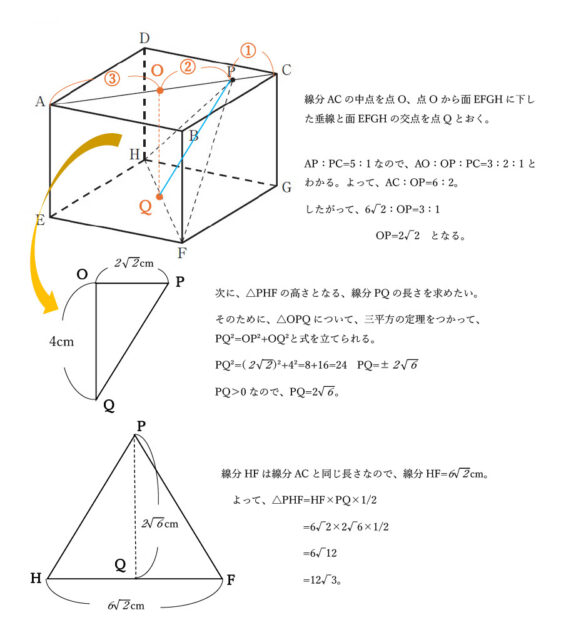
右の図2は,図1において,頂点Fと頂点H,頂点Fと点Pをそれぞれ結んだ場合を表している。
AP : PC=5:1のとき,△FPHの面積は,[ きく ]√[ け ]cm²である。
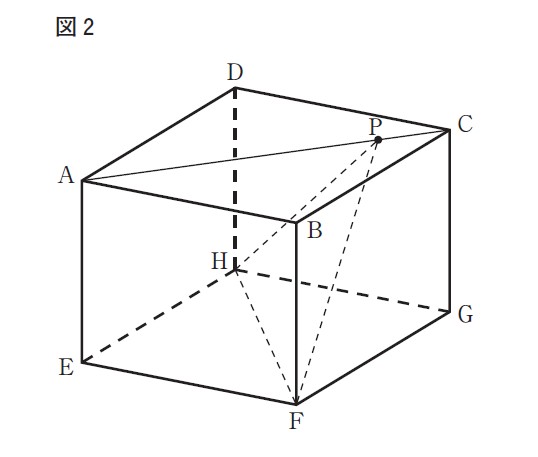
解答 : き:1 く:2 け:3
解説 : 問題文よりAP:PC=5:1なので、線分ACの中点をOとおくと、AO:OP:PC=3:2:1となる。
線分ACと線分OPの長さの比はAC:OP=6:2=3:1である。
線分ACは三平方の定理を使って、AC²=AD²+DC²と表せる。よって、AC²=6²+6²=36+36=72 AC=±√72=±6√2 AC>0より、AC=6√2cmとわかる。AC:OP=3:1なので、6√2:OP=3:1 →3OP=6√2 →3OP×1/3=6√2×1/3 →OP=2√2cm となる。
次に、点Oから面EFGHに下した垂線と面EFGHとの交点を点Qとおく。
△OQPに着目して、三平方の定理を使って、PQ²=OP²+OQ²と式を立てられる。PQ²=(2√2)²+4²=8+16=24 PQ=±2√6 PQ>0なので、PQ=2√6cm。
△PHFの底辺はHFであり、これはACと等しいので、HF=6√2cm。
よって、△PHF=HF×PQ×1/2=6√2×2√6×1/2=6√12=12√3cm³。
したがって、[ き ]は1、[ く ]は2、[ け ]は3が正答となる。