2025年度沖縄学力検査問題過去問【数学】

■問題PDF　

■目次　

■大問１

次の計算をしなさい。

１-１：4 – 11

解答 ：-7

解説 ：4 – 11 = -(11 – 4) = -7

１-２：(- 10) ÷ 2/5

解答 ：-25

解説 ：(- 10) ÷ 2/5 = (- 10) × 5/2 = -50/2 = -25

１-３：(- 2.3) + 4.1　(小数で答えなさい。)

解答 ：1.8

解説 ：(- 2.3) + 4.1 = – 2.3 + 4.1 = 4.1 – 2.3 = 1.8

１-４：3√6 ÷ √2

解答 ：3√3

解説 ：3√6 ÷ √2 = 3√6/2 = 3√3

１-５：3a × (- 2b)²

解答 ：12ab²

解説 ：3a × (- 2b)² = 3a × (- 2b) × (- 2b) = 12ab²

１-６：-(5x – y) + 2(x + 2y)

解答 ：-3x + 5y

解説 ：-(5x – y) + 2(x + 2y) = -5x + y + 2x + 4y = 2x – 5x + y + 4y = -(5 – 2)x + (1 + 4)y = -3x + 5y

■大問２

次の[　　]に最も適する数や式、または記号を入れなさい。

２-１：1次方程式 5x – 2 = 3x + 4 の解は、x = [　　]である。

解答 ：x = 3

解説 ：5x – 2 = 3x + 4　→　5x – 3x = 4 + 2　→　2x = 6　→　x = 3

２-２：連立方程式{ 3x + 2y = -2，　x – y = 6 } の解は、x = [　　]、y = [　　]である。

解答 ：x = 2，y = -4

解説 ：{ 3x + 2y = -2 …①，　x – y = 6 …② }とおく。

[代入法]
②より、x – y = 6　→　x = y + 6 …②’
②’を①に代入して、3(y + 6) + 2y = -2　→　3y + 18 + 2y = -2　→　5y = -2 – 18　→　5y = -20　→　y = -4
y = -4 を②’に代入して、x = (-4) + 6　→　x = 6 – 4　→　x = 2
したがって、x = 2，y = -4

※加減法でも解くことができます。

２-３：(x – 2y)(x + 2y) を展開して整理すると、[　　]である。

解答 ：x² – 4y²

解説 ：乗法公式を使って解く。


(x – 2y)(x + 2y) = x² – 4y²

２-４：3ax² – 2ax を因数分解すると、[　　]である。

解答 ：ax(3x – 2)

解説 ：乗法公式は使わず、共通因数を括りだす。
3ax² – 2ax = ax(3x – 2)　よって、答えは ax(3x – 2)となる。

２-５：2次方程式 3x² – 5x + 1 = 0 の解は、x = [　　]である。

解答 ：x = (5 ±√13)/6

解説 ：この方程式は因数分解ではなく、解の公式で解く。

x = -(-5) ± √(-5)² – 4 × 3 × 1 / 2 × 3　→　x = (5 ± √25 – 12) / 6　→　x = (5 ± √13) / 6　

２-６：√2と3/2の大小関係を式で表すと、[　　]である。次のア～ウから1つ選び、記号で答えなさい。

ア √2 = 3/2　　イ √2 ＜ 3/2　　ウ √2 ＞ 3/2

解答 ：イ

解説 ：3/2について、小数に変形すると 3/2 = 1.5　である。
1.5を根号に入れると、√(1.5)² = √2.25　とわかる。
よって、√2 ＜ √2.25 = 3/2　なので、選択肢イが適当である。

２-７：右の図において ℓ // m のとき、∠x = [　　]°である。

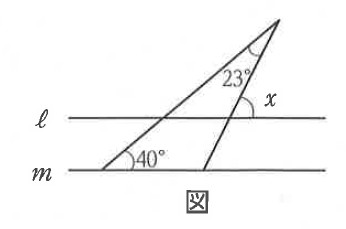
解答 ：∠x = 63°

解説 ：図に、角度などわかる部分を書き込みながら考える。
まず、 ℓ // m より同位角は等しくなる。

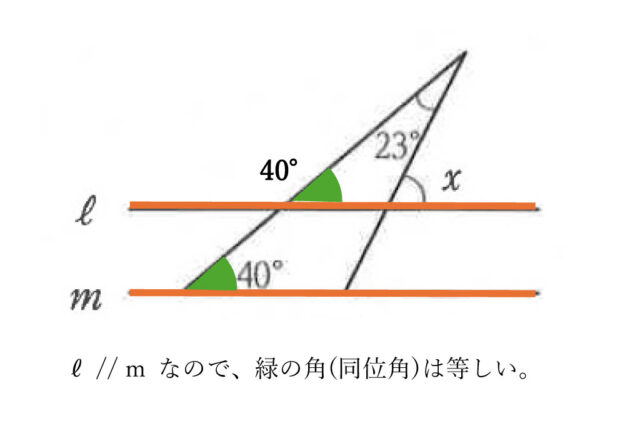
また、外角の定理より、1つの外角は隣り合わない2つの内角の和となる。

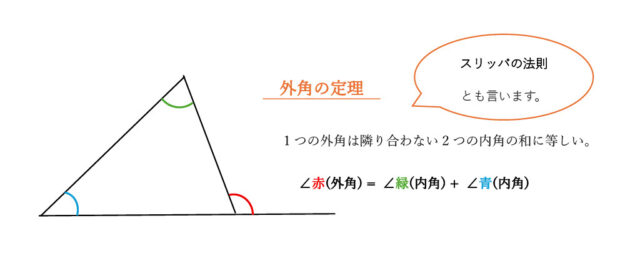
したがって、∠x = 40° + 23°　よって、∠x = 63°　と求められる。

２-８：ある中学校の生徒6人が砲丸投げを行ったところ、下のような結果になった。この6人の砲丸投げの記録の中央値は、[　　]mである。

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
[記録]　　8，7，4，5，4，9　(m)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・

解答 ：6

解説 ：中央値は、データを小さい順に並べたとき、ちょうど真ん中に位置する値のことである。
問題の6人のデータを小さい順に並べると、以下のようになる。

[記録(小さい順)]　　4，4，5，7，8，9　(m)　

よって、中央値は5と7の間にあることになる。
よって、5と7の平均を求めたらよいので、(5 + 7) ÷ 2 = 12 ÷ 2 = 6　したがって、6mとわかる。

２-９：あるアルミ工場で製造した製品から200個を無造作に抽出して検査をすると、不良品の割合が0.03と推定された。この工場で製造された製品8000個に含まれる不良品は、およそ[　　]個であると推定される。次のア～エのうち1つ選び、記号で答えなさい。

ア 240　　イ 600　　ウ 1200　　エ 2400

解答 ：ア

解説 ：問題文より、製品から200個を無作為に抽出して検査したとき、不良品の割合は0.03だったことが読み取れる。この不良品の割合は、検査する製品の個数が増えても変化しないと考えられるので、8000個の製品に含まれる不良品の割合も0.03だと考えられる。

8000 × 0.03 = 80 × 3 = 240　したがって、240個だと求められる。
よって、選択肢アが適当である。

■大問３

下の図は、2017年度、2018年度、2022年度、2023年度について、沖縄県入域観光客数(国内)の月ごとの人数をそれぞれ12か月分調べ、箱ひげ図にまとめたものである。
ただし、沖縄県入域観光客数(国内)とは、沖縄県在住者を除く、沖縄県を訪れた国内客の人数のことである。また、月ごとの人数は千の位を四捨五入しており、単位は万人である。
このとき、次の各問いに答えなさい。

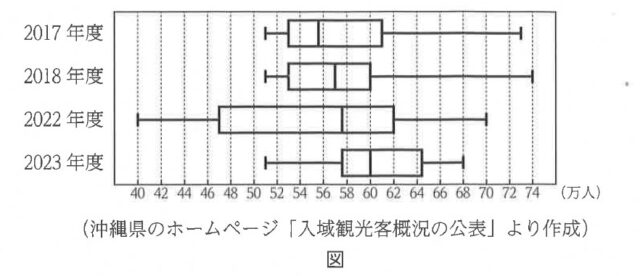
３-１：2018年度のデータについて、第3四分位数を答えなさい。

解答 ：60

解説 ：箱ひげ図より、2018年度のグラフの第3四分位数は60と読み取れる。

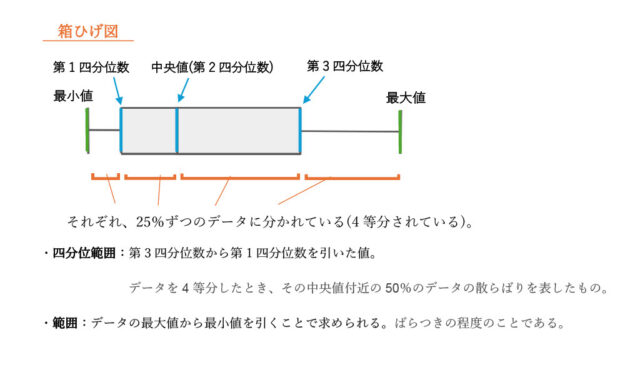
３-２：図から読み取れることとして、必ず正しいといえるものを、次のア～エのうちから1つ選び、記号で答えなさい。

ア 2017年度よりも2018年度の方が、データの四分位範囲が大きい。
イ 4つの年度のうち、データの平均値が最も大きいのは、2018年度である。
ウ 沖縄県入域観光客数(国内)が52万人以下の月は、2022年度よりも2018年度の方が多い。
エ 2023年度において、沖縄県入域観光客数(国内)が60万人以上の月は、6か月以上ある。

解答 ：エ

解説 ：選択肢アについて、2017年度の四分位範囲と2018年度のそれを比較すればよい。2017年度の四分位範囲は61 – 53 = 8。2018年のデータの四分位範囲は、60 – 53 = 7。よって、2017年度の四分位範囲の方が大きいので、選択肢アは不適当。
選択肢イは、この図の箱ひげ図からは平均値は明確にはわからない。よって、選択肢イは不適当である。
選択肢ウに関しても、この図からは読み取れない内容なので不適当。
選択肢エは、2023年度の沖縄県入域観光客数(国内)の中央値は60万人である。中央値(第2四分位数)から最大値までの間にはデータの50％が含まれるので、2023年度の沖縄県入域観光客数(国内)が60万人以上の月は6か月以上あることがわかる。よって、選択肢エは適当である。
したがって、選択肢エが適当である。

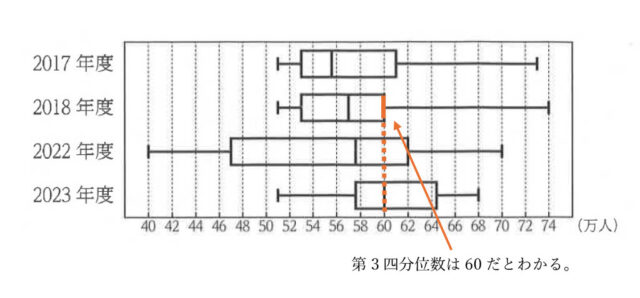
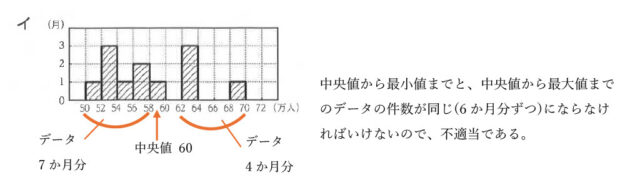
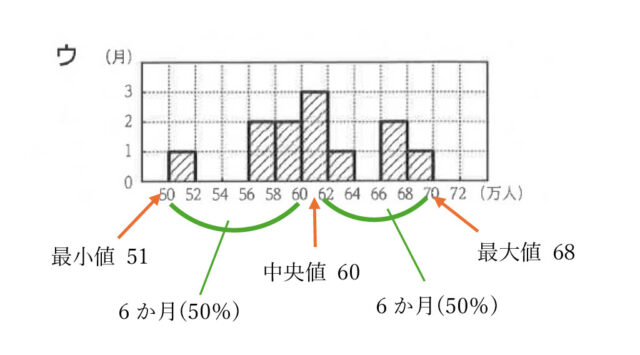
３-３：2023年度の箱ひげ図と同じデータを使ってまとめたヒストグラムとして最も適するものを、次のア～エのうちから1つ選び、記号で答えなさい。なお、50万人以上52万人未満、52万人以上54万人未満のように、階級の幅はいずれも2万人である。

解答 ：ウ

解説 ：2023年度の箱ひげ図より最大値は68万人、最小値は51万人なので、選択肢アとエは不適当である。


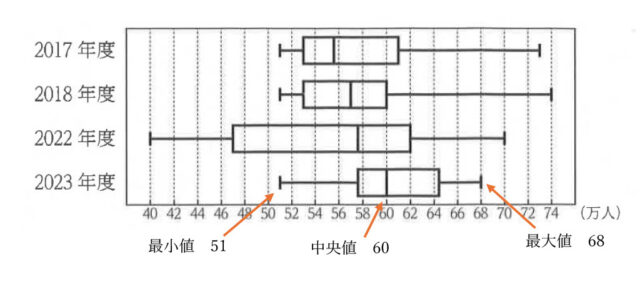
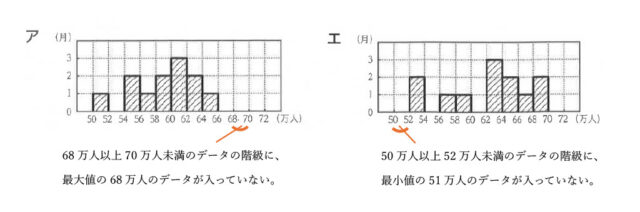
次に2023年度のデータの中央値は、箱ひげ図より60万人と読み取れる。よって、選択肢イは不適当とわかり、選択肢ウが適当だと求められる。

■大問４

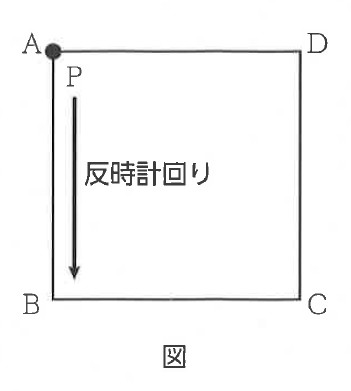
右の図のような正方形ABCDがある。点Pは最初、頂点Aの位置にあり、1つのさいころを投げて、次の規則にしたがって移動する。


・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
規則1　出た目の数だけ正方形の辺に沿って、反時計回りに頂点を1つずつ移動する。
規則2　さいころを2回投げるときは、1回目に移動した場所から、続けて反時計回りに移動する。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・

例えば、さいころを2回投げるとき、1回目に1の目が出たら、点Pは頂点Aから頂点Bに移動し、さらに2回目に2の目が出たら、点Pは頂点Bから頂点Cを通って頂点Dに移動する。
このとき、次の各問いに答えなさい。
ただし、さいころはどの目が出ることも同様に確からしいとする。

４-１：さいころを1回投げて、点Pが頂点Dの位置にある確率を求めなさい。

解答 ：1/6

解説 ：さいころを1回投げて点Pが頂点Dの位置にあるのは、点Pが3回動いたときである。よって、さいころの3の目が出たときの、1通りである。また、さいころの目は、全部で6通りである。

したがって、さいころを1回投げて、点Pが頂点Dの位置にある確率は1/6とわかる。

４-２：さいころを1回投げて、点Pが頂点Bの位置にある確率を求めなさい。

解答 ：1/3

解説 ：さいころを1回投げて、点Pが頂点Bの位置にあるのは、さいころの1の目、または5の目が出たときである。よって、2通りとわかる。また、さいころの目は、全部で6通りである。

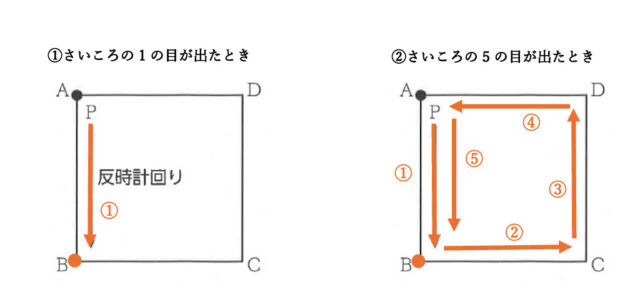
したがって、さいころを1回投げて、点Pが頂点Bの位置にある確率は2/6 = 1/3 と求められる。

４-３：さいころを2回投げて、点Pが頂点Bの位置にある確率を求めなさい。

解答 ：2/9

解説 ：規則2より、「さいころを2回投げるときは、1回目に移動した場所から、続けて反時計回りに移動する。」とのことである。よって、点Pは最小で2回、最大で12回動くことがわかる。

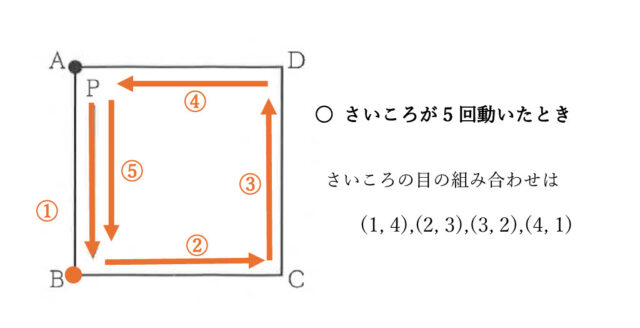
次に、さいころを投げて点Pが頂点Bの位置にあるときは、5回または9回動いたときである。
・さいころが5回動いたとき
　2回のさいころの目の組み合わせは、(1, 4)、(2, 3)、(3, 2)、(4, 1)　

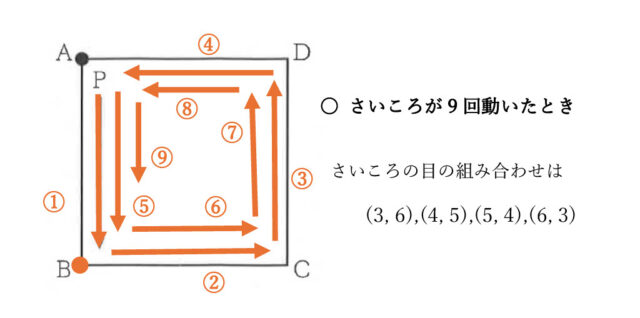
・さいころが9回動いたとき
　2回のさいころの目の組み合わせは、(3, 6)、(4, 5)、(5, 4)、(6, 3)　

したがって、さいころを2回投げて点Pが頂点Bの位置にあるのは、全部で8通りである。
2つのさいころの目の出方は全部で36通りである。

以上より、さいころを2回投げて、点Pが頂点Bの位置にある確率は、8/36 = 2/9である。

■大問５

下の図は、学校の体育館でシートの上に椅子を並べている様子である。椅子の前脚から後脚までの幅は50cmであり、椅子と椅子の間隔をa cm空けて規則的に椅子を並べていく。はじめにシートの先端から10cm空けて最初の椅子を置き、最後の椅子を置いたときに、椅子の後脚がちょうどシートの端にくるように、椅子を並べるものとする。
このとき、次の各問いに答えなさい。

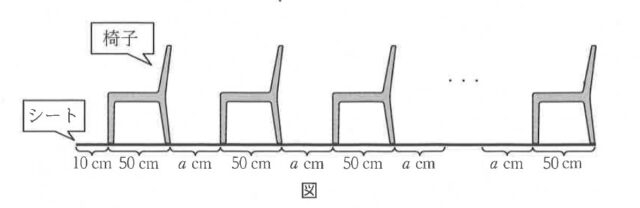
５-１：下の表は、a = 40 のときの椅子の数と椅子を並べるのに必要なシートの長さの関係を示した表の一部である。
このとき、下の表の[　　]にあてはまる最も適する数を答えなさい。

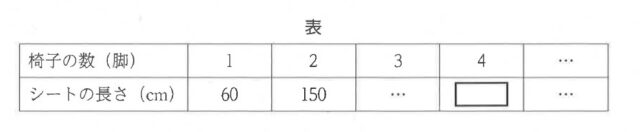
解答 ：330

解説 ：表の[　　]は、椅子を4脚並べるときに必要なシートの長さである。 まず、図で椅子を4脚並べたときを考える。

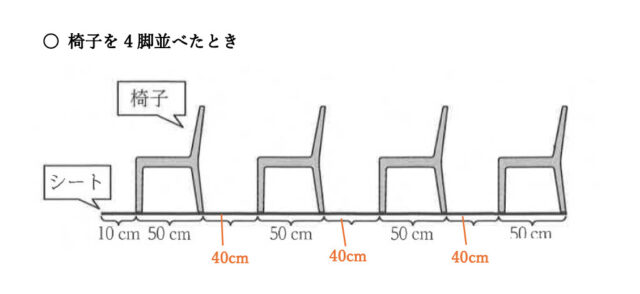
よって、10cm + 50cm × 4脚 + 40cm × 3 = 10 + 200 + 120 = 330　したがって、330cmと求められる。

５-２：a = 40 とする。椅子の数をx脚、椅子を並べるのに必要なシートの長さをy cmとしたとき、yをxの式で表しなさい。

解答 ：y = 90x – 30

解説 ：a = 40 なので、椅子と椅子との間隔が40cmだとわかる。

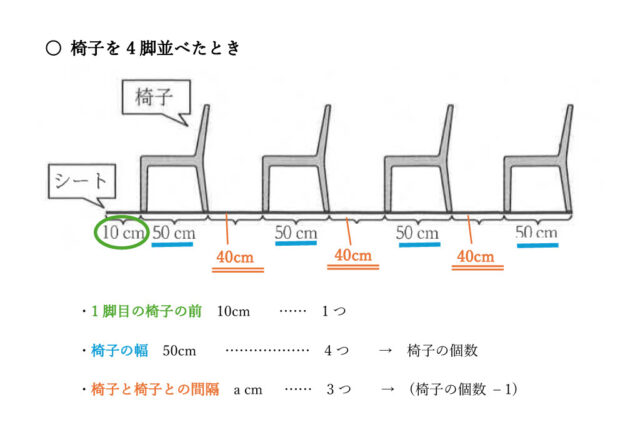
椅子を並べるのに必要なシートの長さに関係しているのは、1脚目の椅子の前の10cmと、椅子の幅50cm、椅子と椅子との間隔の40cmである。

問1も参考にすると、1脚目の椅子の前の10cmは1つ、椅子の幅は椅子の個数、椅子と椅子との間隔は椅子の個数から1少ない数である。加えて、椅子の個数はx脚、椅子と椅子の間隔は、(x – 1)つある。
よって、y = 10 + (50 × x) + {40 × (x – 1)}　→　y = 10 + 50x + 40x – 40　→　y = 90x – 30
したがって、椅子の数をx脚、椅子を並べるのに必要なシートの長さをy cmとしたとき、y = 90x – 30 と表せる。

５-３：長さ3180cmのシートに40脚の椅子を並べるとき、aの値を求めなさい。

解答 ：a = 30

解説 ：長さ3180cmのシートに40脚の椅子を並べるので、問2の式を応用して計算できる。
3180cm = 10cm + (50cm × 40脚) + {a cm × (40 – 1)}　→　3180 = 10 + 2000 + a × 39　→　3180 = 2010 + 39a　→　39a = 3180 – 2010　→　39a = 1170　→　39a × 1/39 = 1170 × 1/39　→　a = 30　したがって、a = 30　と求められる。

■大問６

右の図のように、円周上に4点A、B、C、Dがある。弦AB、弦CDを利用して、円の中心Pを定規とコンパスを使って作図しなさい。

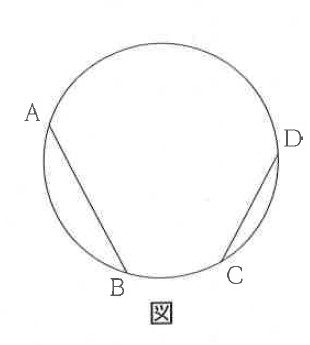
ただし、円の中心を示す記号をかき入れ、作図に用いた線は消さずに残しておくこと。

解答 ：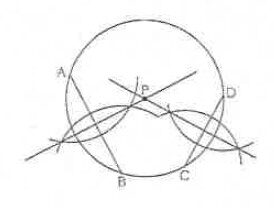

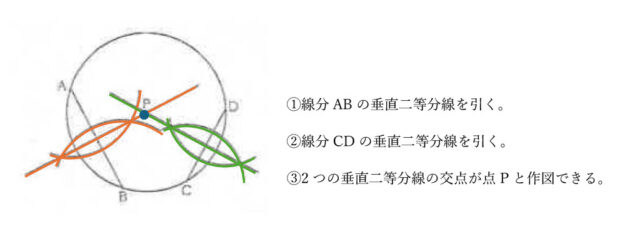
解説 ：まず、コンパスで弦ABの垂直二等分線をかく。点Aにコンパスの針を置いてかいた曲線と、点Bにコンパスの針を置いた曲線の2つの交点を通る直線を引くことで作図できる。
同様に、弦CDの垂直二等分線もかく。この2つの垂直二等分線の交点が、この円の中心Pである。

■大問７

雄太さんと桃子さんは、次の【宿題】について考えた。下の【会話】は、2人が話し合っている場面である。

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
【宿題】
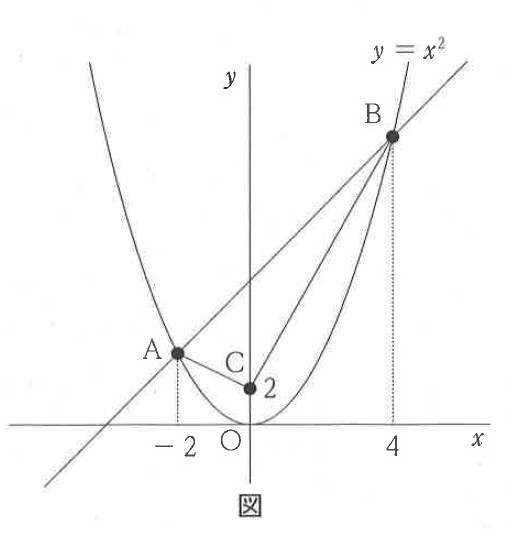
　右の図のように、関数 y = x² のグラフ上にx座標が-2である点Aと、x座標が4である点Bがある。y軸上にy座標が2である点Cをとったときの、△ABCの面積を求めなさい。
　また、△ABCと△ABPの面積が等しくなるような点Pをx軸上にとるとき、点Pの座標を求めなさい。
　ただし、原点Oから点(0, 1)、点(1, 0)までの長さをそれぞれ1cmとする。

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
【会話】
雄太：点Aの座標はA(-2, [ ア ])になるね。同じように点Bの座標もわかるね。
桃子：2点の座標がわかったから、2点A、Bを通る直線の式が、y = [ イ ]であることが求められたよ。
雄太：直線の式がわかったから、△ABCの面積が[ ウ ]cm²になることがわかるね。
桃子：点Pの座標を求めるためには△ABCの底辺をABとしたときに、△ABCの高さと△ABPの高さが同じになるような点Pをx軸上にとればよさそうだね。
雄太：点Cを通り直線ABと平行な直線を使えば、点Pの座標が求められるね。
桃子：そうだね。点Cのほかにもy軸上に点Dをとって、△ABCの面積と△ABDの面積が等しくなるようにできるね。点Dを通り直線ABと平行な直線を使用することでも問題の条件を満たす点Pがx軸上にとれるから、宿題の答えとなる点Pは2点あるということだね。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
このとき、次の各問いに答えなさい。

７-１：[ ア ]にあてはまる最も適する数を答えなさい。

解答 ：(2, [ 4 ])

解説 ：[ ア ]は、点Aのy座標である。
点Aは、y = x² のグラフ上の点で、且つ x = -2 の点である。よって、x = -2 を代入して、y = (-2)²　→　y = 4　よって、[ ア ]には4が当てはまる。

７-２：[ イ ]にあてはまる最も適する式を答えなさい。

解答 ：y = 2x + 8

解説 ：[ イ ]については、2点ABを通る直線の式である。
問1より、点Aの座標は(-2, 4)である。点Bは【宿題】より、x座標が4である点なので、問1で点Aの座標を求めたときと同様に計算する。x = 4 を代入して、y = 4²　→　y = 16　よって、点Bの座標は(4, 16)と計算できる。

次に、点A(-2, 4)と点B(4, 16)の2つの点を通る直線の式を考える。
まず、一次関数の基本の式は、y = ax + b にそれぞれの点を代入する。
4 = -2a + b …①
16 = 4a + b …②
①より、b = 2a + 4 これを②に代入して、16 = 4a + (2a + 4)　→　16 = 4a + 2a + 4　→　6a = 16 – 4　→　6a = 12　→　a = 2。これをb = 2a + 4 に代入して、b = 2 × 2 + 4　→　b = 4 + 4　→　b = 8　よって、点A、Bを通る式は、 y = 2x + 8　と求められる。

したがって、[ イ ]には 2x + 8 が当てはまる。

７-３：[ ウ ]にあてはまる最も適する数を答えなさい。

解答 ：18

解説 ：[ ウ ]には、△ABCの面積が当てはまる。

まず、直線ABとy軸との交点をTとおく。点Tのy座標は直線ABの切片なので、直線ABの式 y = 2x + 8 より、点Tの座標は(0, 8)である。

次に、△ABCの面積を、y軸で左右2つの三角形に分けて面積を求める。

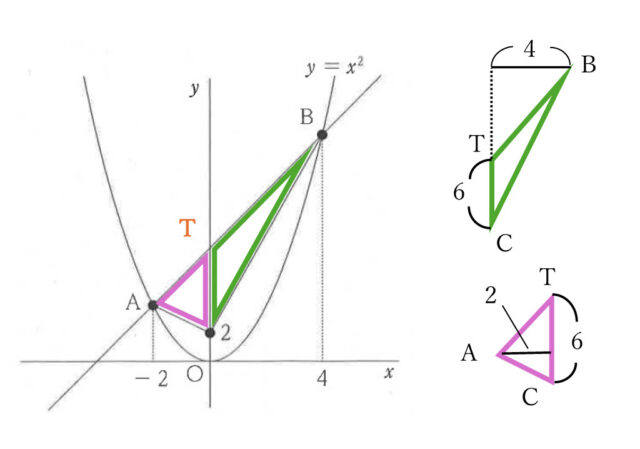
・△TACの面積について
　辺TCを底辺と考えると、8 – 2 = 6 より、底辺は6cm。高さは点Aからy軸までの距離なので、点Aのx座標より、2cmとわかる。よって、△TAC = 6 × 2 ÷ 2 = 6　したがって、6cm²である。
・△BTCの面積について
　△TACと同様に辺TCを底辺とすると、6cm。高さは点Bからy軸までの長さなので、4cmである。△BTC = 6 × 4 ÷ 2 = 12　よって、12cm² とわかる。

△ABC = △TAC + △BTC なので、△ABC = 6 + 12 = 18　以上より、△ABCの面積は、18cm² と求められる。

７-４：△ABCと△ABPの面積が等しくなるようなx軸上の点Pの座標を2つ求めなさい。

解答 ：P(-1, 0)，(-7, 0)

解説 ：桃子さんの言葉から、△ABCと△ABPの面積が等しくなるようなx軸上の点Pは2点あることがわかる。

①太郎さんの考えをもとに。
「点Cを通り直線ABと平行な直線を使えば、点Pの座標が求められる」と言っているので、ここでは等積変形の考え方を使うことがわかる。

まず、直線ABの式は y = 2x + 8 なので、点Cを通り直線ABに平行な直線の傾きは 2 とわかる。よって、y = 2x + b に点C(0, 2)を代入すると、2 = 2 × 0 + b　→　b = 2　よって、点Cを通り直線ABに平行な直線の式は y = 2x + 2 と求められる。
【宿題】より、点Pはx軸上の点なので、 y = 2x + 2 とx軸との交点を求めればよい。x軸は、y = 0 なので、 0 = 2x + 2　→　 2x = -2　→　 x = -1　したがって、点Pの座標の1つは(-1, 0)　と計算できる。


②花子さんの言葉をもとに。
花子さんは「y軸上に点Dをとって、△ABCの面積と△ABDの面積が等しくなるようにできる」と言っている。この部分を踏まえて、問3で△ABCの面積を求めた際と同じように考えて、△ABCの面積と等しくなるような△ABDの点Dを考える。TCとDCの長さは6cmなので、点Dの座標は(0, 14)とわかる。

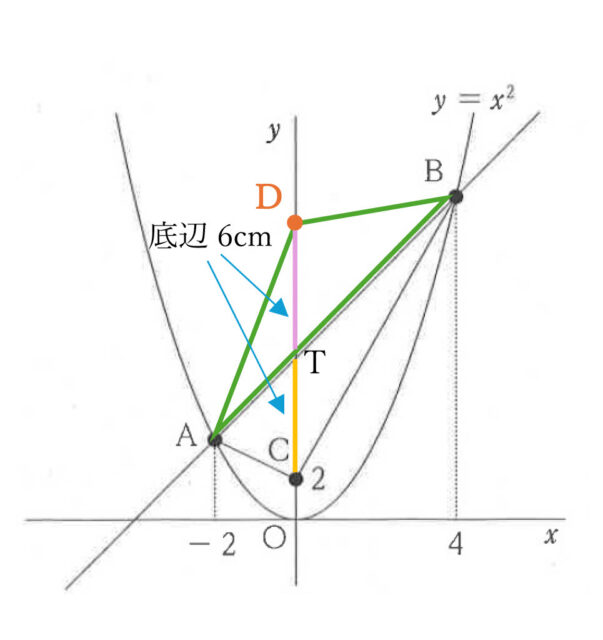
その後、花子さんは「点Dを通り直線ABと平行な直線を使用することでも問題の条件を満たす点Pがx軸上にとれる」と言っているので、点Dを通る直線を求める。直線ABの傾きは 2 で、点D(0, 14)を通るので、点Dを通り直線ABに平行な直線の式は y = 2x + 14 と求められる。
点Pはx軸上の点なので、y = 2x + 14 とy = 0との交点は、0 = 2x + 14　→　2x = -14　→　x = -7　よって、点Pの座標のもう1つは(-7, 0)と求められる。


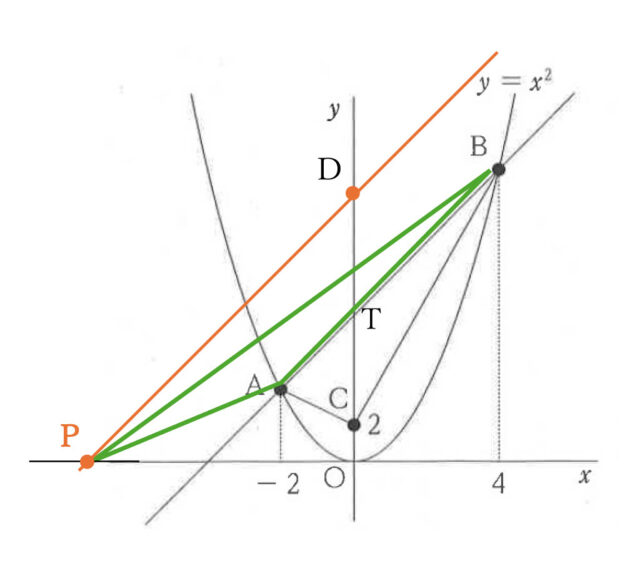
以上より、点Pの2つの座標は(-1, 0)と(-7, 0)である。

■大問８

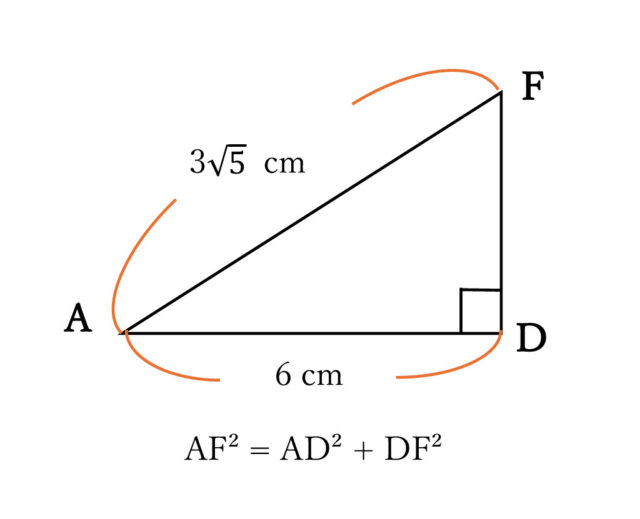
８-１：線分DFの長さを求めなさい。

解答 ：3 cm

解説 ：辺DFは△ADFの1辺である。また、△ADFは直角三角形なので、三平方の定理を使えば、辺DFの長さを求めることができる。

AF² = AD² + DF²　→　(3√5)² = 6² + DF²　→　45 = 36 + DF²　→　DF² = 45 – 36　→　DF² = 9　→　DF = ±3　DF＞0なので、DF = 3　よって、線分DFの長さは3cmと求められる。

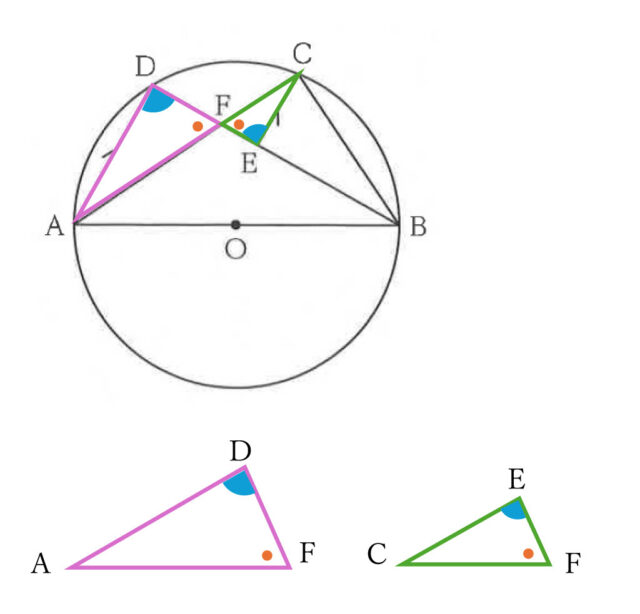
８-２：△ADF∽△CEFとなることを証明しなさい。

解答 ：[証明]
△ADFと△CEFにおいて、
平行線の錯角は等しいので、∠DAF = ∠ECF・・・①
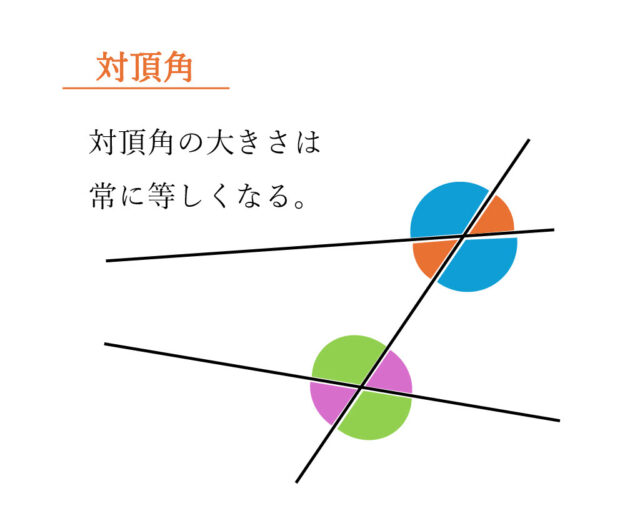
対頂角は等しいので、∠AFD = ∠CFE・・・②
①、②より、2組の角がそれぞれ等しいので、
　△ADF ∽ △CEF　　　　　　　　　　[証明終]

解説 ：※解答とほぼ重複しています。

[証明]
△ADFと△CEFにおいて、
　平行線の錯角は等しいので、∠DAF = ∠ECF・・・①　

　対頂角は等しいので、∠AFD = ∠CFE・・・②　

①、②より、2組の角がそれぞれ等しいので、
　　　△ADF ∽ △CEF　　　　　　　　[証明終]

８-３：△ABDの面積を求めなさい。

解答 ：63/2 cm²

解説 ：△ABDの面積を求めるうえで、まずは∠ADBに着目する。
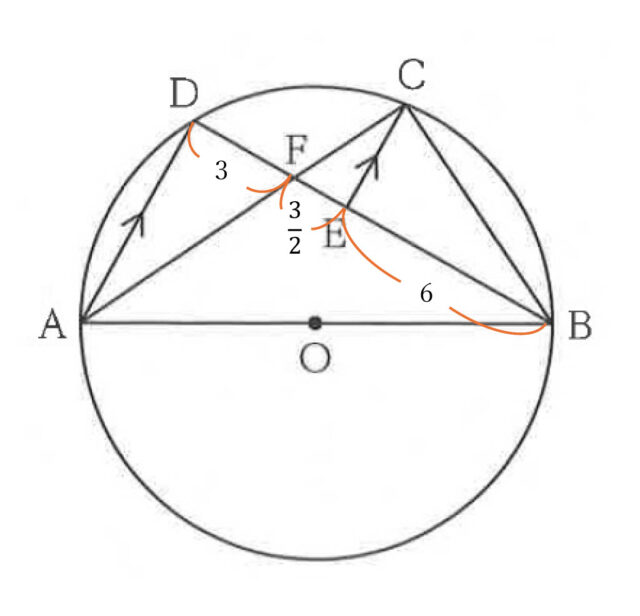
線分ABは円Oの直径なので、円周角の定理より、∠ADB = 90°とわかる。よって、△ABDは直角三角形であり、問題文より辺DAは6cmとわかっている。 よって、辺DBの長さが分かれば、△ABDの面積を求めることができる。


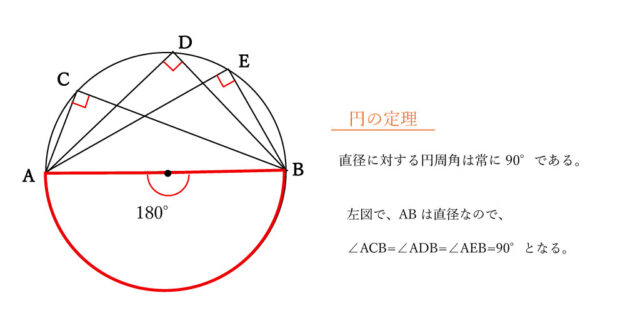
△ADFと△BECにおいて
　仮定より　DA = EB　・・・①
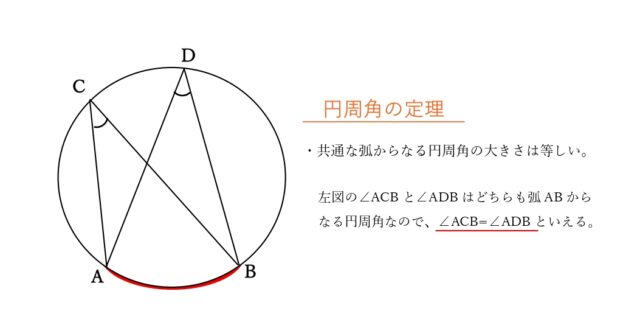
　円周角の定理より、同じ弧からなる円周角は等しいので、
　　　　　　∠DAF = ∠EBC　・・・②
　平行線の錯角は等しいので、
　　　　　　∠FDA = ∠CEF・・・③
　③より、∠CEB = 180° – ∠CEF = 180° – 90° = 90°　・・・④
　③、④より、∠FDA = ∠CEB　・・・⑤
　①、②、⑤より、
　2組の辺とその間の角は等しいので、△ADF ≡ △BEC　



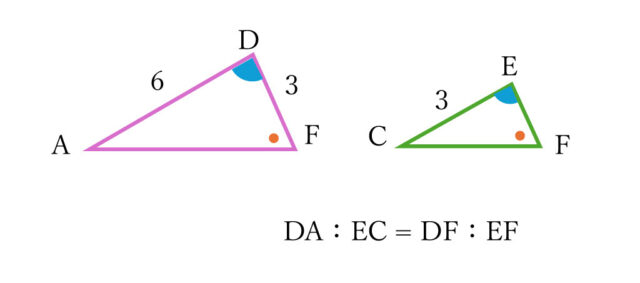
△ADF ≡ △BECよりCE = 3 で、且つ△ADF ∽ △CEFなので、
　DA：EC = DF：EF　→　6：3 = 3：EF　→　6EF = 9　→　EF = 9/6 = 3/2

DB = DF + EF + EB なので、DB = 3 + 3/2 + 6 = 9 + 3/2 = 21/2　と求められる。


最後に、△ABDの面積は、△ABD = 21/2 × 6 ÷ 2 = 63/2

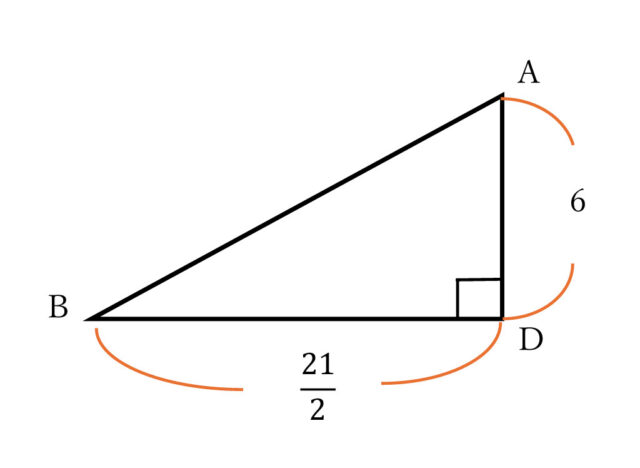
以上より、△ABDは 63/2 cm²　とわかる。

■大問９

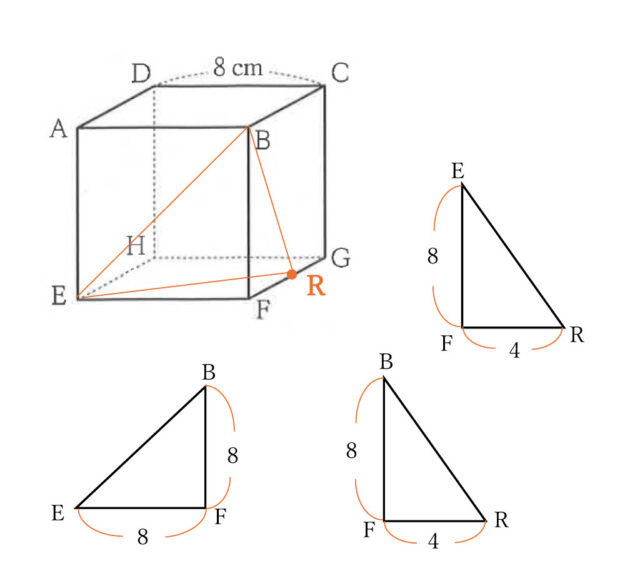
右の図1のように、1辺が8cmの立方体ABCD-EFGHがある。
このとき、次の各問いに答えなさい。

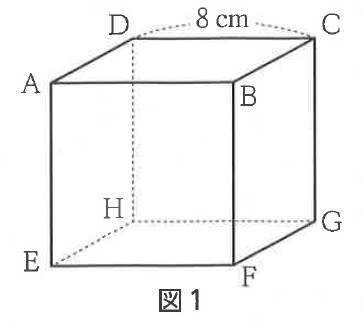
９-１：図1の立方体の体積を求めなさい。

解答 ：512 cm³

解説 ：立方体の体積は、1辺 × 1辺 × 1辺 で求められる。
図1の立方体の1辺は8cmなので、8 × 8 × 8 = 512　よって、512cm³ とわかる。

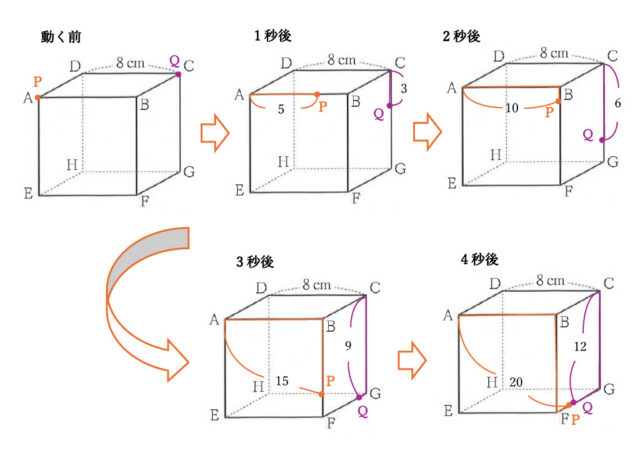
９-２：右の図2は、図1の立方体において、2点P、Qがそれぞれ頂点A、Cを同時に出発し、立方体の辺上を動きながら、頂点を移動する様子を示した図である。
点Pは毎秒5cmの速さで立方体の頂点を、　頂点A→頂点B→頂点F→頂点G→頂点C　と移動し、点Qは毎秒3cmの速さで立方体の頂点を、　頂点C→頂点G→頂点F→頂点B→頂点A　と移動する。
2点P、Qが重なる点をRとし、この立方体を3点B、E、Rを通る平面で切り、頂点Fを含む立体をSとする。
このとき、次の各問いに答えなさい。

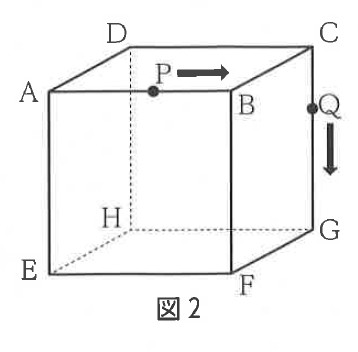
９-２(１)：2点P、Qが重なるのは出発して何秒後か求めなさい。

解答 ：4 秒後

解説 ：問題文より、点Pの速さは毎秒5cm、点Qは毎秒3cmである。
よって、図を描いて考えると、2点P、Qが重なるのは出発してから4秒後である。

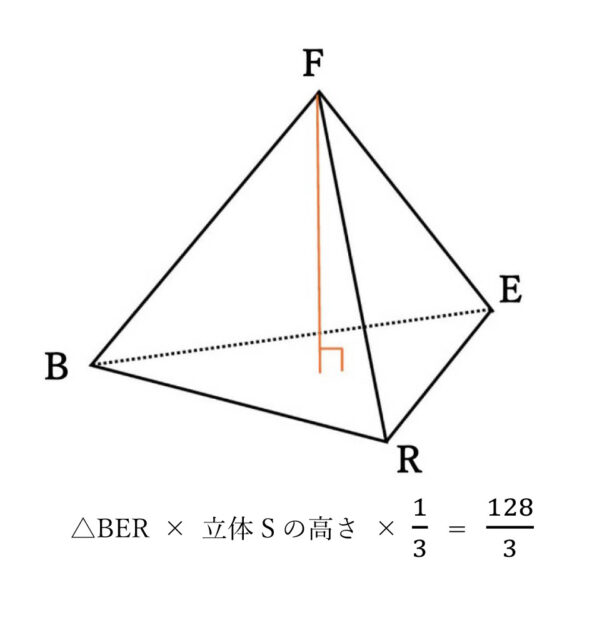
９-２(２)：立体Sの体積を求めなさい。

解答 ：128/3 cm³

解説 ：問題文より、立体Sは2点P、Qが重なる点をRとし、この立方体を3点B、E、Rを通る平面で切り、頂点Fを含む立体のことである。以下の図より、立体Sは三角錐だとわかる。


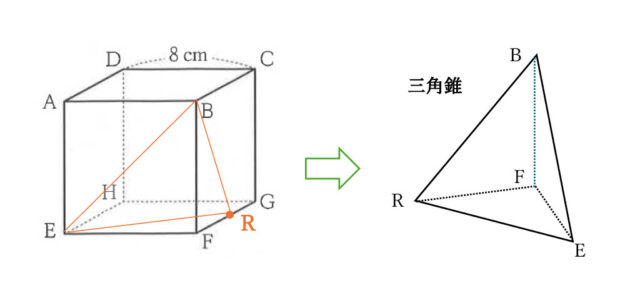
△REFの面を底面とすると、辺BFが高さと捉えられる。

よって、8 × 4 × 1/2 × 8 × 1/3 = 16 × 8 × 1/3 = 128/3　したがって、128/3 cm³ と求められる。

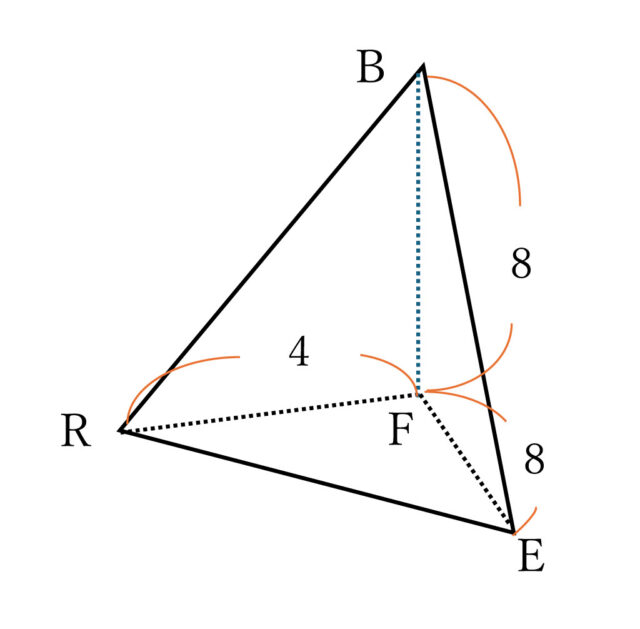
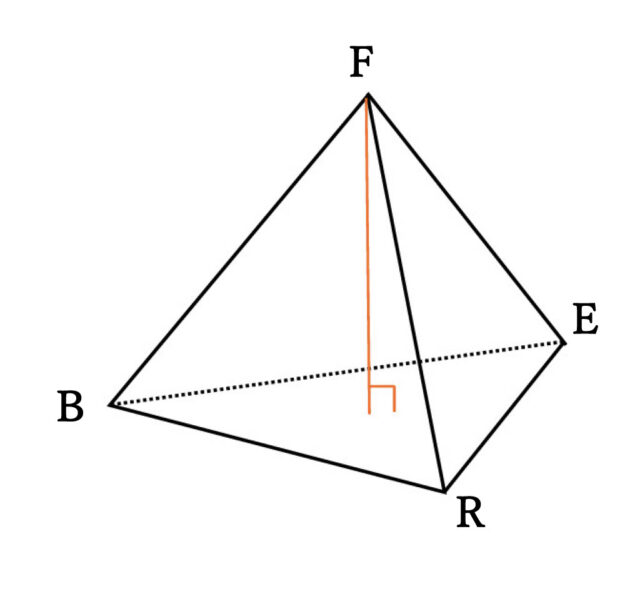
９-２(３)：立体Sにおいて、△BERを底面としたときの高さを求めなさい。

解答 ：4√6/3 cm

解説 ：△BERを底面としたとき、点Fから△BERに垂直におろした線が高さとなる。


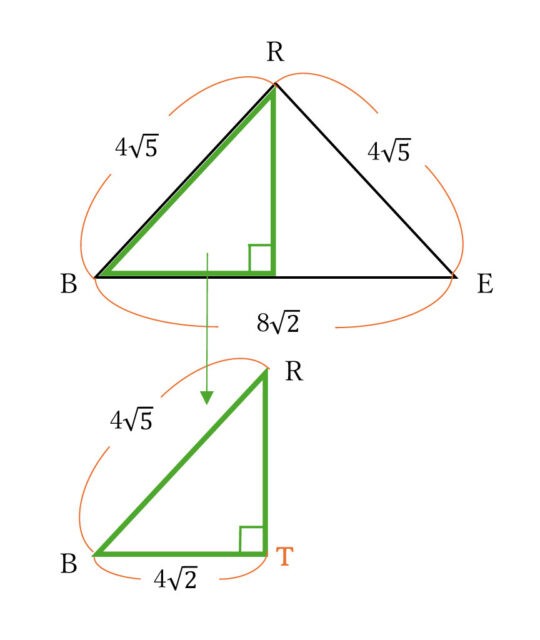
まずは、△BERに着目し、三平方の定理を活用して△BERの3つの辺の長さを計算する。


・辺BEについて
　BE² = BF² + EF²　→　BE² = 8² + 8²　→　BE² = 64 + 64　→　BE² = 128　→　BE = ±√128　→　BE = ±8√2　BE＞0より、BE = 8√2　とわかる。
・辺BRについて
　BR² = BF² + FR²　→　BR² = 8² + 4²　→　BR² = 64 + 16　→　BR² = 80　→　BR = ±√80　→　BR = ±4√5　BR＞0より、BR = 4√5
・辺ERについて
　ER² = EF² + FR²　→　ER² = 8² + 4²　→　ER² = 64 + 16　→　ER² = 80　→　ER = ±√80　→　ER = ±4√5　ER＞0より、ER = 4√5

点Rから辺BEに垂直に引いた線と、辺BEとの交点をTとおくと、△BERは二等辺三角形なので、BT = 4√2 である。よって、△RBTにおいて三平方の定理を用いて、RTの長さを求める。RB² = RT² + BT²　→　(4√5)² = RT² + (4√2)²　→　80 = RT² + 32　→　RT² = 80 – 32　→　RT² = 48　RT = ±4√3　RT＞0より、RT = 4√3　とわかる。したがって、△BERの面積は、8√2 × 4√3 × 1/2 = 16√6　よって、16√6 cm² と求められる。


立体Sの高さをx とおくと、(2)より立体Sの体積は128/3 cm³ なので、△BER × 立体Sの高さ × 1/3 = 128/3 と式が作れる。よって、16√6 × x × 1/3 = 128/3　→　16√6/3x = 128/3　→　16√6/3x × 3 = 128/3 × 3　→　16√6x = 128　→　x = 128 × 1/16√6　→　x = 8/√6　→　x = 8√6/6　→　x = 4√6/3　したがって、立体Sの高さは、4√6/3 cm　とわかる。

---

■大問１０

---

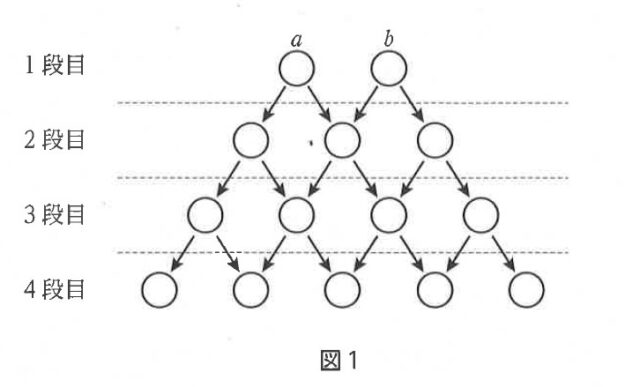
下の図1のように並べられた〇の中に、次の規則にしたがって数を記入する。


・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
規則1　1段目には2つの自然数 a、b を記入する。
規則2　2段目以降は、左端に a、右端に b を記入し、それ以外は左上の数と右上の数の和を記入する。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・

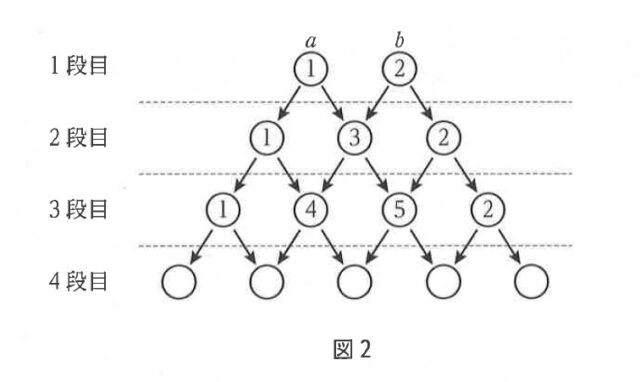
下の図2は、a = 1、b = 2 として、規則にしたがって数を3段目まで記入したときの様子である。

このとき、次の各問いに答えなさい。

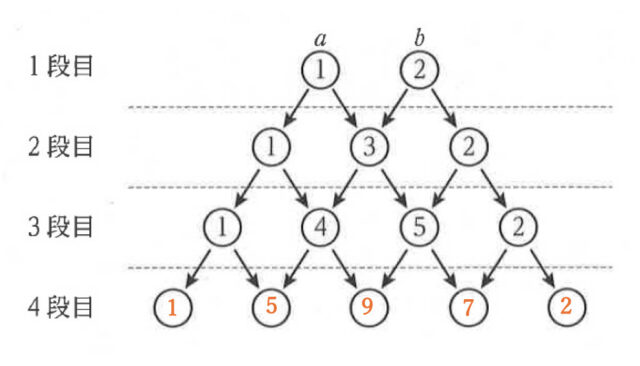
１０-１：a = 1、b = 2 のとき、4段目に記入される5個の数を左から順に答えなさい。

解答 ：1、5、9、7、2

解説 ：図2を使って、a = 1、b = 2 のとき、4段目に記入される5個の数を書き込むと、図のようになる。よって、4段目に記入される5つの数は、左から順に1、5、9、7、2 とわかる。

１０：夏美さんは a、bを様々な値に変えて1段目から4段目まで数を記入し、その結果を考察し、次の予想した。

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
1段目の数 a、bをどのように変えても、次のことが成り立つ。
　予想1　2段目の3個の数の和は、1段目の2個の数の和の2倍となる。
　予想2　3段目の4個の数の和は、1段目の2個の数の和の4倍となる。
　予想3　4段目の5個の数の和は、1段目の2個の数の和の8倍となる。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・

真美さんは、まず予想1が成り立つことを次のように説明した。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
予想2の説明
　1段目の2個の数を a、bとすると、その和は a、b
　2段目の3個の数を a、b を用いて左から順に表すと、a、a + b、b
　その和は a + (a + b) + b = 2a + 2b = 2(a + b)
　よって、2段目の3個の数の和は、1段目の2個の数の和の2倍となる。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・

次に、予想2が成り立つことを次のように説明した。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
予想2の説明
　1段目の2個の数を a、bとすると、その和は a、b
　3段目の4個の数を a、b を用いて左から順に表すと、a、[ ア ]、[ イ ]、b
　その和は a + ([ ア ]) + ([ イ ]) + b = 4a + 4b = 4(a + b)
　よって、3段目の4個の数の和は、1段目の2個の数の和の4倍となる。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・

１０-２：上の[ ア ]、[ イ ]にそれぞれあてはまる最も適する式を答え、真美さんの予想2の説明を完成させなさい。ただし、式は同じ文字の項をまとめ、最も簡単な形で表すこと。

解答 ：[ ア ]　2a + b [ イ ]　a + 2b

解説 ：予想1より、1段目の2個の数を a、bとすると、2段目の3個の数は左から順に a、a + b、b と表せる。このことを踏まえて、3段目の4個の数は以下の図のように表せる。よって、左から順に a、2a + b、a + 2b、b である。


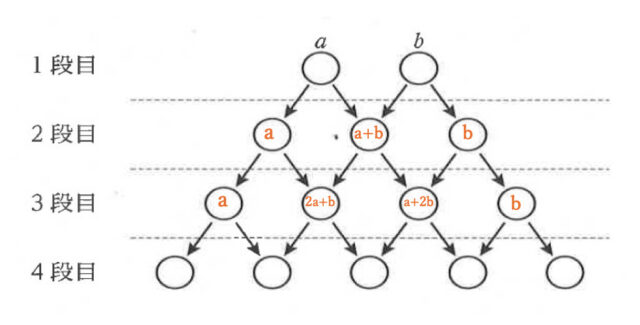
・[ ア ]について
[ ア ]は3段目の、左から2番目の数なので、2a + b とわかる。
・[ イ ]について
[ イ ]は3段目の左から3番目の数で、a +2b である。

１０-３：予想3が成り立つことを、1段目の2個の数を a、b とし、4段目の5個の数を aとb を用いて表すことによって説明しなさい。

解答 ：(説明)
1段目の2個の数を a、b とすると、その和は a + b
4段目の5個の数を aとb を用いて左から順に表すと、
　　　a、3a + b、3a + 3b、a + 3b、b
その和は、a + (3a + b) + (3a + 3b) + (a + 3b) + b
= 8a + 8b
= 8(a + b)
よって、4段目の5個の数の和は、1段目の2個の数の和の8倍となる。
　　　　　　　　　　　　　　　　(説明終)

解説 ：※答えと重複する部分も多いです。

予想3は、「4段目の5個の数の和は、1段目の2個の数の和の8倍となる。」という部分である。
1段目の2個の数を a、b とすると、4段目までの数は aとb を用いて図のように表せる。


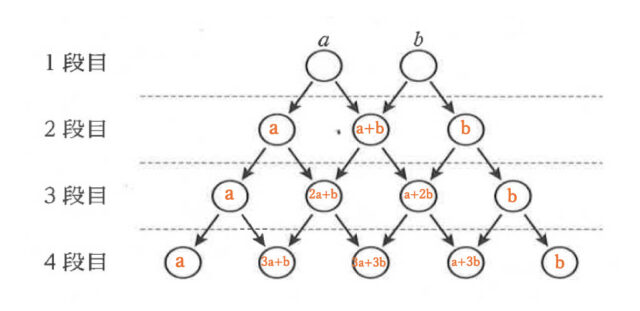
(説明)
1段目の2個の数を a、b とすると、その和は a + b
4段目の5個の数を aとb を用いて左から順に表すと、
　　　a、3a + b、3a + 3b、a + 3b、b
これらの数の和は、a + (3a + b) + (3a + 3b) + (a + 3b) + b
　　　　　　　　= a + 3a + b + 3a + 3b + a + 3b +b
　　　　= 8a + 8b
　　　　= 8(a + b)
1段目の数の和は a + b なので、4段目の数の和の 8(a + b) は、 (a + b)の4倍だとわかる。
したがって、4段目の5個の数の和は、1段目の2個の数の和の8倍といえる。
　　　　　　　　　　　　　　　　　　　　　　(説明終)

１０-４：a = 18、b = 32 のとき、 1段目から4段目までの〇の中に記入された14個の数の和を求めなさい。

解答 ：750

解説 ：まずは、1～4段目の、それぞれの和を求める。


・1段目の2個の数の和
　1段目の2つの数は aとbなので、a + b = 18 + 32 = 50
・2段目の3個の数の和
　2段目の3個の数は、a と a+b と b なので、これらの和は a + (a + b) + b = 2a + 2b = 2(a + b) = 2 × 50 = 100
・3段目の4個の数の和
　3段目の4個の数は、左から順に a、2a + b、a + 2b、b である。これらの数の和は、 a + (2a + b) + (a + 2b) + b = a + 2a + b + a + 2b + b = 4a + 4b = 4(a + b) = 4 × 50 = 200
・4段目の5個の数の和
　4段目の5個の数の和は、問3より、8(a + b) である。よって、a = 18、b = 32を 8(a + b) に代入して、8(18 + 32) = 8 × 50 = 400

以上より、1～4段目までの14個の数の和は、50 + 100 + 200 + 400 = 750　したがって、750とわかる。