■問題PDF
令和7年度_学力検査問題過去問【大阪】- 数学A
令和7年度_学力検査問題過去問【大阪】- 数学A 解答
■目次
大問1
大問2
大問3
大問4
■大問1
次の計算をしなさい
1-1:6−(−7)
解答 : 13
解説 : 6−(−7)=6+7=13
1-2:9/2÷(−9/4)
解答 : -2
解説 : 9/2÷(−9/4)=9/2×(−4/9)=−2
1-3:5×3^2
解答 : 45
解説 : 5×(3×3)=5×9=45
1-4:2(x+y)+x−13y
解答 : 3x-11y
解説 : 分配法則で展開すると 2x+2y+x−13y = 3x−11y
1-5:7x^2×4x
解答 : 28x^2
解説 : 7x^2×4x=(7×4)×(x^2×x)=28x^3
1-6:5√(5)−√(20)
解答 : 3√5
解説 : √(20) = 2√5 より, 5√5 − √20 = 5√5 − 2√5 = 3√5
■大問2
次の問いに答えなさい
2-1:a=4 のとき, 6a+5 の値を求めなさい
解答 : 29
解説 : a=4 を 6a+5 に代入すると, 6×4+5=24+5=29
2-2:次のア〜エのうち, 無理数であるものはどれですか. 一つ選び, 記号を○で囲みなさい
ア 1/3 イ √3 ウ 0.3 エ √9

解答 : イ
解説 : √3 は無理数. 他は有理数(1/3, 0.3, √9=3)
2-3:比例式 x:8=5:4 を満たす の値を求めなさい.
解答 : 10
解説 : x:8=5:4 より, 4x=8×5, 4x=40, x=10
2-4:次のア〜エのうち, yがxに反比例するものはどれですか. 一つ選び, 記号を○で囲みなさい.
ア 1本の値段が100円のペンをx本買ったときの代金y円
イ 30枚の色紙からx枚を使ったときの残りの色紙の枚数y枚
ウ 1500mの道のりを分速xmで歩いたときにかかる時間y分
エ xmLのお茶を5人で同じ量に分けたときの一人当たりのお茶の量ymL
解答 : ウ
解説 : ア:y=100x (比例)
イ: y=30−x (1次関数)
ウ: y= 1500/x (反比例)
エ:y= 5x (比例)
2-5:右のデータは, 6人の生徒それぞれが1学期に読んだ本の冊数を値の小さい順に並べたものである. 6人の生徒それぞれが読んだ本の冊数の範囲を求めなさい.
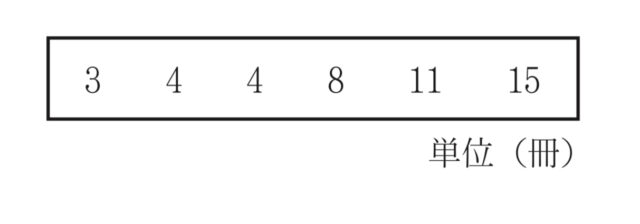
解答 : 12冊
解説 : 範囲は最大値から最小値を引いたものより, 15−3=12 (冊)
2-6:連立方程式
2x+3y=11
x-3y=10
を解きなさい.
解答 : x=7, y=-1
解説 : ①:2x+3y=11
②:x−3y=10
①+②より, 3x=21, x=7
x=7 を②に代入すると, 7−3y=10, −3y=3, y=−1
したがって, x=7, y=−1
2-7:二つの箱A, Bがある. 箱Aには奇数の書いてある3枚のカード 1, 3, 5が入っており, 箱Bには偶数の書いてある3枚のカード 4, 6, 8 が入っている. A, Bそれぞれの箱から同時にカードを1枚ずつ取り出すとき, 取り出した2枚のカードに書いてある数の和が7である確率はいくらですか. A, Bそれぞれの箱において, どのカードが取り出されることも同様に確からしいものとして答えなさい.
解答 : 2/9
解説 : Aから1枚, Bから1枚取り出すときの組み合わせは, 3×3=9通り. 和が7になる組み合わせは, (1,6)と(3,4)の2通り. したがって, 確率は2/9となる.
2-8:二次方程式 x^2−8x+12=0 を解きなさい.
解答 : x=2, x=6
解説 : 因数分解すると, (x−2)(x−6)=0 したがって, x=2, x=6
2-9:右の図において, mは関数 y=ax^2 (aは定数)のグラフを表す. Aはm上の点であり, その座標は (5,7) である. aの値を求めなさい.
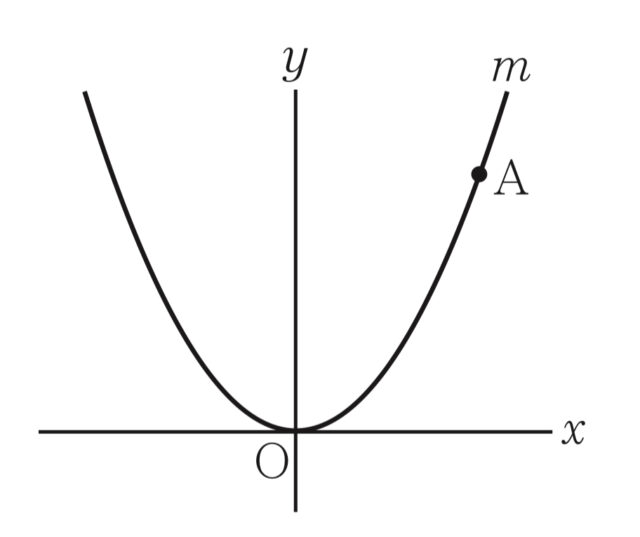
解答 : 7/25
解説 : 点A (5,7) が関数 y=ax^2のグラフ上にあるので, x=5, y=7 を代入し, 7=a×5^2, 7=25a, a=7/25
右の図において, 立体ABCD-EFGHは直方体であり, AB=AD=4 cm, AE=5 cm である.
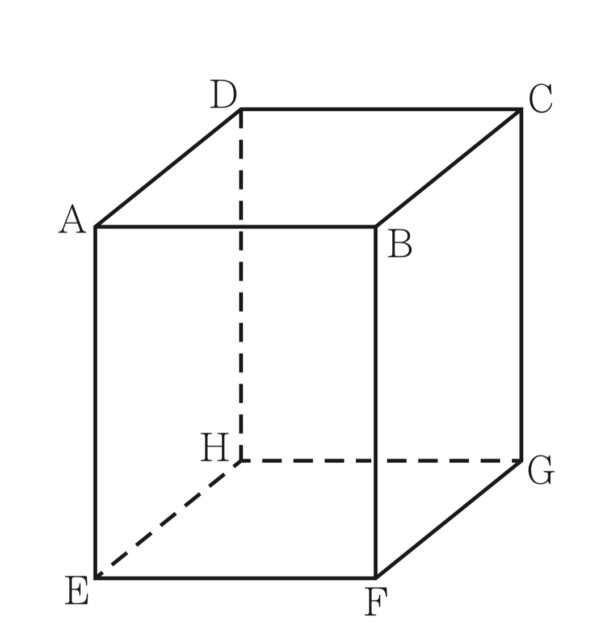
2-10①: 次のア〜エのうち, 辺AEとねじれの位置にある辺はどれですか. 一つ選び, 記号を○で囲みなさい.
ア 辺AB
イ 辺BF
ウ 辺EH
エ 辺FG
解答 : エ
解説 : 辺AEとねじれの位置にあるのは, 辺に平行でも交わってもいない辺. 辺AEとねじれの位置にあるのは, 辺FG, 辺DC, 辺HG, 辺BC
2-10②:立体 ABCDEFGHの表面積を求めなさい.
解答 : 112
解説 : (底面と上面)×(側面4つ)={(4×4)×2}+{(4×5)×4}=16×2+20×4=32+80=112 cm^2
■大問3
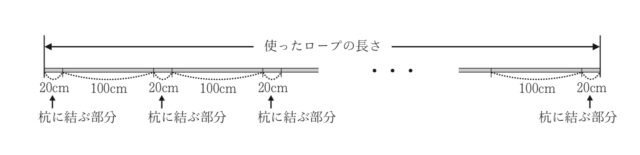
体育祭の準備のため, Fさんはグラウンドで先生と一緒に, 杭を打ってロープを張ることになった. ロープは, それぞれの杭の上部にある輪に結びながら張っていく. 杭に結ぶ部分のロープの長さはすべて20cmであり, ロープはたるみなく張るものとする.
Fさんは, 杭を100cm間隔で打ってロープを張ることにした. 下の図は, Fさんが使ったロープを表す模式図である. 「杭の本数」がェ本のときの「使ったロープの長さ」を ycmとする. x=2のときy=140であるとし, xの値が1増えるごとにりの値は120ずつ増えるものとする.
次の問いに答えなさい.
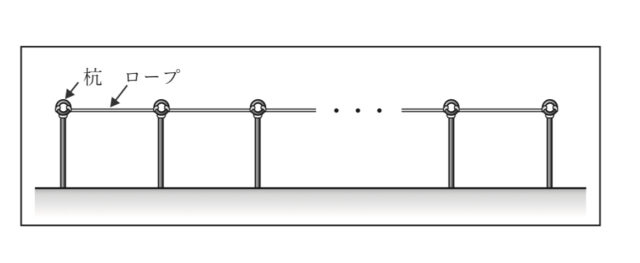
3-1:次の表は, xとyとの関係を示した表の一部である. 表中の (ア), (イ)に当てはまる数をそれぞれ書きなさい.
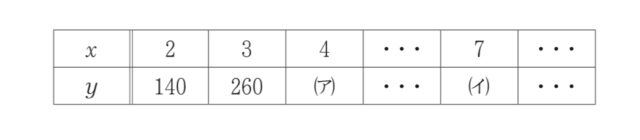
解答 : ア=380, イ=740
解説 : 先に式を求める. xとyの関係が1次関数 y=ax+b で表されると仮定し, xが1増えるごとにyが120ずつ増える. よってa=120, y=120x+b となる. x=2 のとき y=140 より, 140=120×2+b, 140=240+b, b=−100 となる. したがって, y=120x−100
(ア) x=4 のときのyの値:y=120×4−100=480−100=380
(イ) x=7 のときのyの値:y=120×7−100=840−100=740
3-2:xを2以上の自然数として, yをxの式で表しなさい.
解答 : y=120x-100
3-3:y=1580となるときのxの値を求めなさい.
解答 : 14
解説 : (2)の式に y=1580 を代入. 1580=120x−100, 20x=1580+100, 120x=1680, x=14
■大問4
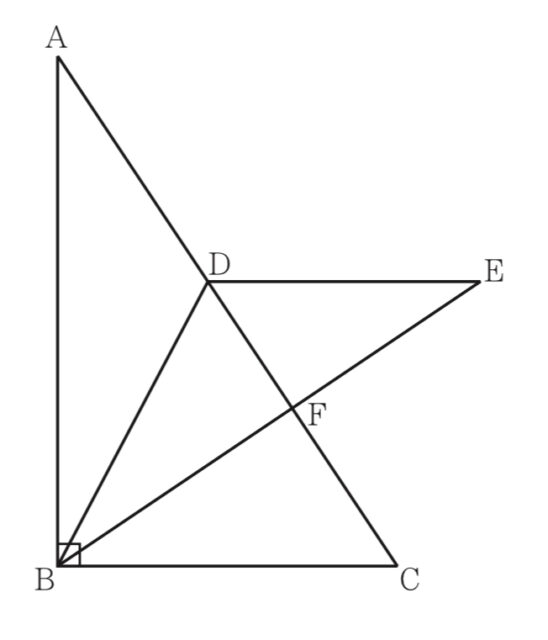
右の図において, △ABCは∠ABC=90 の直角三角形であり, AB=3cmである. Dは, 辺AC上にあってA, Cと異なる点である. EDB=△ADBであり, DE // BCである. Fは, 辺EBと辺ACとの交点である. BC = x cmとし, x>0とする.
次の問いに答えなさい.
4-1:△ADBを, ある直線を対称の軸として対称移動すると, △EDBにぴったり重ねることができる. 次のア〜エの直線のうち, このときの対称の軸はどれですか. 一つ選び, 記号を○で囲みなさい.
ア 直線 DB
イ 直線 AB
ウ 直線 AC
エ 直線DE
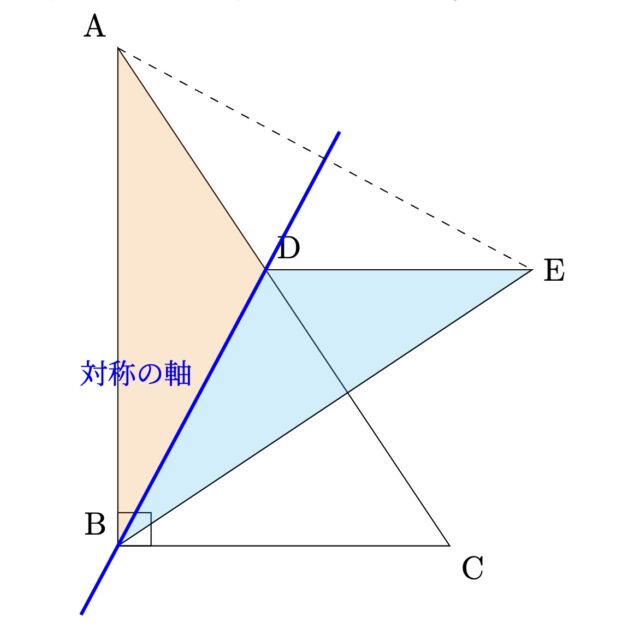
解答 : ア
解説 : △ADBを対称移動すると△EDBに重なることから, 対称の軸はDB
4-2:△ABCの面積を を用いて表しなさい.
解答 : 3x/2
解説 : △ABCは直角三角形より, 面積は1/2×AB×BC で求められる. AB=3cm, BC=xcmより, 面積は 1/2×3×x=3x/2
4-3:次は, △ABC∽ABFCであることの証明である. a, b に入れるのに適している「角を表す文字」をそれぞれ書きなさい. また, c【 】から適しているものを一つ選び, 記号を○で囲みなさい. △ABCと BFCにおいて ∠ACB= a (共通) △ADB≡△EDB だから ∠CAB=∠DEB DE // BCであり, 平行線の錯角は等しいから ∠b = ∠DEB い, う より∠CAB=∠b あ, え より, c【ア 1組の辺とその両端の角 イ 2組の辺の比とその間の角 ウ 2組の角】がそれぞれ等しいから △АВС ≡△BFC
解答 : a=BCF, b=CBF, ウ
解説 : aには共通の角である∠BCFが入る. DE // BCより, 錯角は等しいことからbは ∠CBF = ∠DEB となる. 「い, う より∠CAB=b∠CBF」とあることから, ∠CABと∠CBFが等しく, 「あ, え より」とあるのでcには「ウ 2組の角」が入る.
4-4:x=2であるときの線分BFの長さを求めなさい. 答えを求める過程がわかるように, 途中の式を含めた求め方も説明すること.
解答 : (6√13)/13
解説 : x=2のとき, BC=2cmとなる. △ABCは直角三角形であるため, 三平方の定理より AC = √(AB² + BC²) = √(3² + 2²) = √(9+4) = √13(AC>0)である. △ABC ∽ △BFC であるため, 対応する辺の比は等しい. AB:BF = BC:FC = AC:BC の関係から, 3:BF = √13:2 を用いる. √13 × BF = 3 × 2, √13 × BF = 6, BF = 6/√13となる. 分母を有理化し, BF = (6√13)/13







