2025年度大阪学力検査問題過去問【数学B】

■問題PDF　

■目次　

■大問１

次の計算をしなさい

1-1:6×(−1)−3 ^2

解答 ： -15

解説 ： 6×(-1)-3^2 = -6 – 9 = -15

1-2:4(5a+2b)−7(2a+b)

解答 ： 6a+b

解説 ： 4(5a+2b)-7(2a+b) = 20a + 8b – 14a – 7b = 6a + b

1-3:24x^2÷3xy×(-1y^2/2)

解答 ： -4xy

解説 ： 24x^2÷3xy×(-1/2 y^2) = (24/3)x^(2-1)y^(1-1) × (-1/2 y^2) = -4xy^2

1-4:x(x+10)−(x+3)(x−1)

解答 ： 8x+3

解説 ： x(x+10)-(x+3)(x-1) = x^2 + 10x – (x^2 + 2x – 3) = x^2 + 10x – x^2 – 2x + 3 = 8x + 3

1-5:(2√7+√2)(2√7-√2)

解答 ： 26

解説 ： (2√7+√2)(2√7-√2) = (2√7)^2 – (√2)^2 = 4×7 – 2 = 28 – 2 = 26

■大問２

次の問いに答えなさい

2-1:a=4, b=-5 のとき、a^2-3b の値を求めなさい

解答 ： 31

解説 ： a^2-3b = 4^2 – 3×(-5) = 16 + 15 = 31

2-2:二次方程式 x^2+x-42=0 を解きなさい

解答 ： x=-7, x=6

解説 ： x^2+x-42=0 を因数分解すると、(x+7)(x-6)=0 となる。よって x = -7, 6

2-3:3<√n<3√2 を満たす自然数nの個数を求めなさい

解答 ： 8

解説 ： 各辺を2乗すると、3^2 < (√n)^2 < (3√2)^2 となる。9 < n < 9×2 なので 9 < n < 18。これを満たす自然数nは 10, 11, 12, 13, 14, 15, 16, 17 の8個である。

2-4:関数 y=ax^2(a は定数)について、xの値が-1から5まで増加するときの変化の割合が16であるとき、aの値を求めなさい

解答 ： 4

解説 ： 変化の割合 = (yの変化量)/(xの変化量) = (a×5^2 – a×(-1)^2)/(5 – (-1)) = (25a – a)/6 = 24a/6 = 4a。これが16より、4a = 16, a = 4

2-5:右の図は、正四面体の展開図である。右の展開図を組み立てて 正四面体をつくったとき、次のア~オのうち、辺ABとねじれの位置にある辺はどれですか。一つ選び、記号を○で囲みなさい。
ア 辺CD
イ 辺CE
ウ 辺DE
エ 辺DF
オ 辺EF

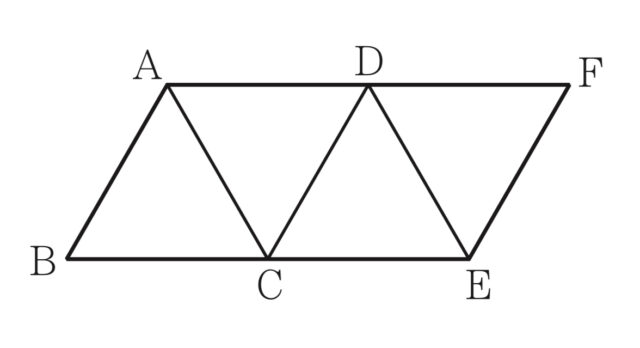
解答 ： ア

解説 ： 展開図を組み立てると、辺ABとねじれの位置にあるのは辺CE

2-6:A、B二つのさいころを同時に投げ、Aのさいころの出る目の数をa、Bのさいころの出る目の数をbとするとき、2a+bの値が5の倍数である確率はいくらですか。1から6までのどの目が出ることも同様に確からしいものとして答えなさい

解答 ： 7/36

解説 ： 全ての目の出方は 6×6=36通り。2a+bが5の倍数になる組み合わせを考える。2a+bが5, 10, 15となる場合。 (a,b)=(1,3), (2,1), (3,4), (4,2), (5,5), (6,3) の6通り。したがって確率は 6/36 = 1/6である。

2-7:右のデータは、9人の生徒それぞれが1学期に読んだ本の冊数を示したものである。9人の生徒それぞれが読んだ本の冊数の中央値が8冊であり、四分位範囲が6冊であるとき、データ中のxの値を求めなさい

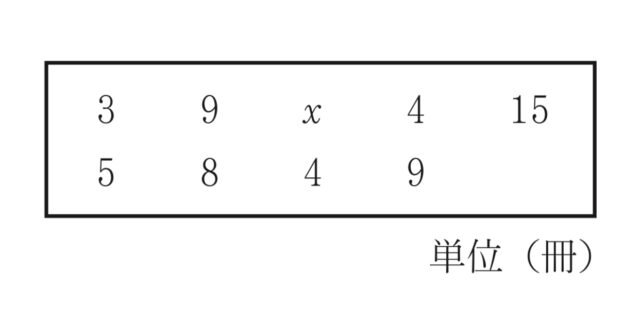
解答 ： 11

解説 ： 小さい順に並べると、x以外の既知のデータは 3, 4, 4, 5, 8, 9, 9, 15 となる。9人の中央値は、小さい方から5番目の値。問題文より中央値が8冊なので、5番目の値は8 。四分位範囲は第3四分位数(Q3)から第1四分位数(Q1)を引いた値であり、問題文より6冊 。データが9個の場合、Q1は2番目と3番目の値の平均、Q3は7番目と8番目の値の平均。 もしxが9より大きく15より小さい位置にあると仮定すると、データは 3, 4, 4, 5, 8, 9, 9, x, 15 と並ぶ。この場合、Q1 = (4+4)/2 = 4 となり、Q3 = (9+x)/2 となる。四分位範囲は Q3 – Q1 = (9+x)/2 – 4 である。これが6に等しいので、(9+x)/2 – 4 = 6, (9+x)/2 = 10, 9+x = 20, x = 11

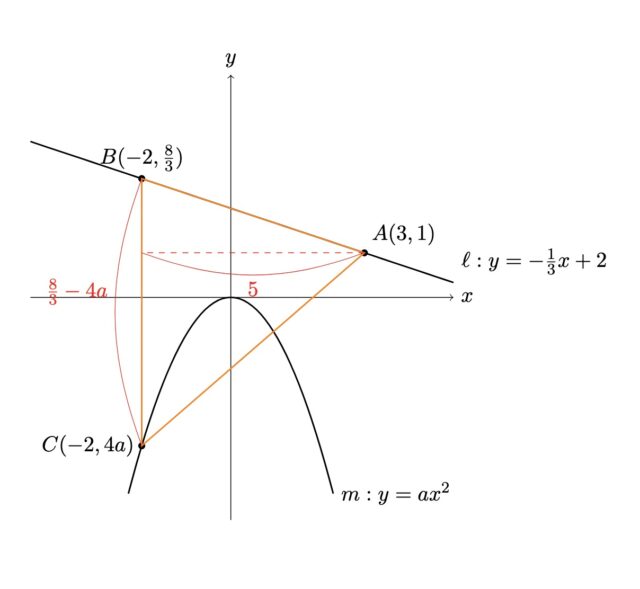
2-8:右の図において、mは関数 y=ax^2(aは負の定数)のグラフを表し、lは関数 y=-1/3x+2のグラフを表す。A、Bはl上の点であって、Aのy座標は1であり、Bのx座標は-2である。Cは、Bを通りy軸に平行な直線とmとの交点である。CとAとを結ぶ。△ABCの面積は15cmである。aの値を求めなさい。答えを求める過程がわかるように、途中の式を含めた求め方も説明すること。 ただし、原点から点 (1.0)までの距離、原点から 点(0.1)までの距離はそれぞれ1cmであるとする。

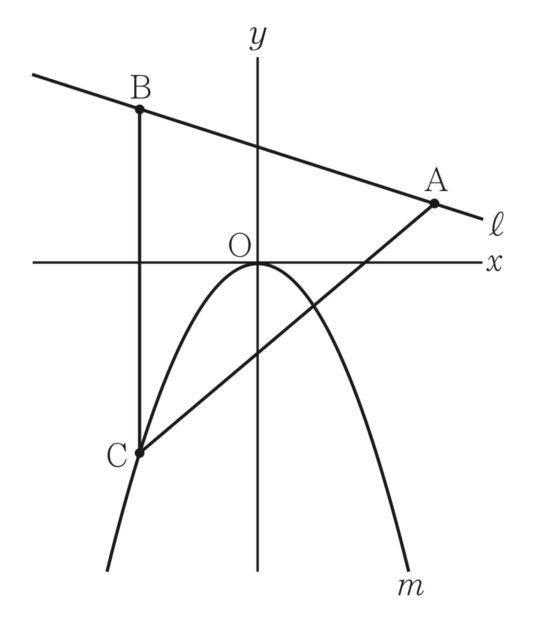
解答 ： -5/6

解説 ： Bがl上の点であることから、Bのx座標は-2をlに代入し、B(-2, 8/3). また、BとCのy座標は等しく、Cはy=ax^2上の点であることから、C(-2, 4a). AからBCへの垂線を下ろし、△ABCの高さとして考える。高さはAとBのx座標の差より、高さ=3-(-2)=5. 底辺はBC=8/3-4a. よって△ABCの面積が15cm^2であることから、△ABC=1/2×5×(8/3-4a)=15, 20/3-10a=15, a=-5/6.

■大問３

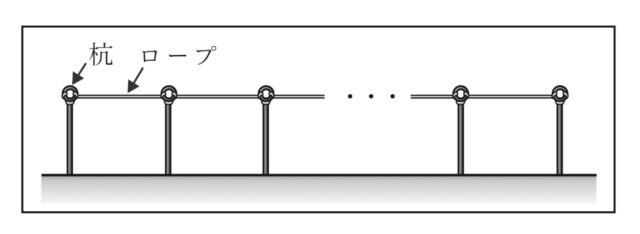
体育祭の準備のため、FさんとGさんはそれぞれグラウンドの別の場所で先生と一緒に、杭を打ってロープを張ることになった。ロープは、それぞれの杭の上部にある輪に結びながら張っていく。杭に結ぶ部分のロープの長さはすべて20cmであり、ロープはたるみなく張るものとする。Fさんは、杭を100cm間隔で打ってロープを張ることにした。図1は、Fさんが使ったロープを表す模式図である。「杭の本数」が2本のとき「使ったロープの長さ」は140cmであるとし、「杭の本数」が1本増えるごとに「使ったロープの長さ」は120cmずつ長くなるものとする。(これを 【Fさんの張り方】とする。)Gさんは、抗を130cm間隔で打ってロープを張ることにした。図Ⅱは、Gさんが使ったロープを表す模式図である。「杭の本数」が2本のとき「使ったロープの長さ」は170cmであるとし、「杭の本数」が1本増えるごとに「使ったロープの長さ」は150cmずつ長くなるものとする。(これを 【Gさんの張り方】 とする。)次の問いに答えなさい。

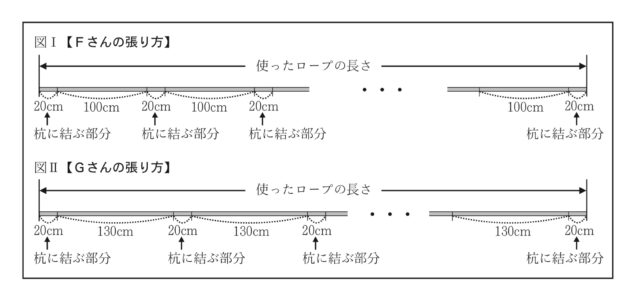
【Fさんの張り方】において、「杭の本数」が本のときの「使ったロープの長さ」をycmとする

3-1①:次の表は、xとyとの関係を示した表の一部である。表中の（ア）、(イ）に当てはまる数をそれぞれ書きなさい

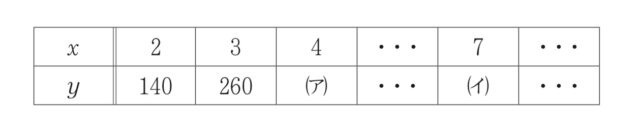
解答 ： ア=380, イ=740

解説 ： 先に式を求める。xとyの関係が1次関数 y=ax+b で表されると仮定し、xが1増えるごとにyが120ずつ増える。よってa=120, y=120x+b となる。x=2 のとき y=140 より、140=120×2+b, 140=240+b, b=−100 となる。したがって、y=120x−100
(ア) x=4 のときのyの値：y=120×4−100=480−100=380
(イ) x=7 のときのyの値：y=120×7−100=840−100=740

3-1②:xを2以上の自然数として、yをxの式で表しなさい。

解答 ： y=120x-100

3-1③:y=1580となるときのxの値を求めなさい

解答 ： 14

解説 ： (2)の式に y=1580 を代入。1580=120x−100, 20x=1580+100, 120x=1680, x=14

3-2:Fさんは【Fさんの張り方】 で。本の杭を打ってロープを張り、Gさんは 【Gさんの張り方】でも本の 杭を打ってロープを張った。2人が打った杭の本数の合計が38本であり、Fさんが使ったロープの長さと Gさんが使ったロープの長さが同じであるとき、s、しの値をそれぞれ求めなさい

解答 ： sの値：21
tの値：17

解説 ： sはFさんの杭の本数とするとFさんの張り方のロープの長さはy_F=120s−100
tはGさんの杭の本数とするとGさんの張り方のロープの長さはy_G=150t−130
問題文より s+t=38⋯① と y_F=y_Gより、120s−100=150t−130⋯②。②を整理し 120s−150t=−30, 4s−5t=−1⋯③。①より s=38−t, ③に代入し4(38−t)−5t=-1, 152−4t−5t=−1, −9t=−153, t=17。t=17 を①に代入s=38−17=21。したがって、s=21, t=17

■大問４

次の【Ⅰ】、【Ⅱ】に答えなさい

【Ⅰ】 図 において、A、B、Cは点○を中心とする円の周上の異なる3点である。3点A、B、Cを結んでできる △ABCはAB=ACの二等辺三角形であり、頂角∠BACは鋭角である。Dは、Bから線分ACにひいた垂線と 線分ACとの交点である。Eは、直線OCと円○との交点のうちCと異なる点である。Fは、線分ECと線分AB との交点である。EとAとを結ぶ。次の問いに答えなさい。

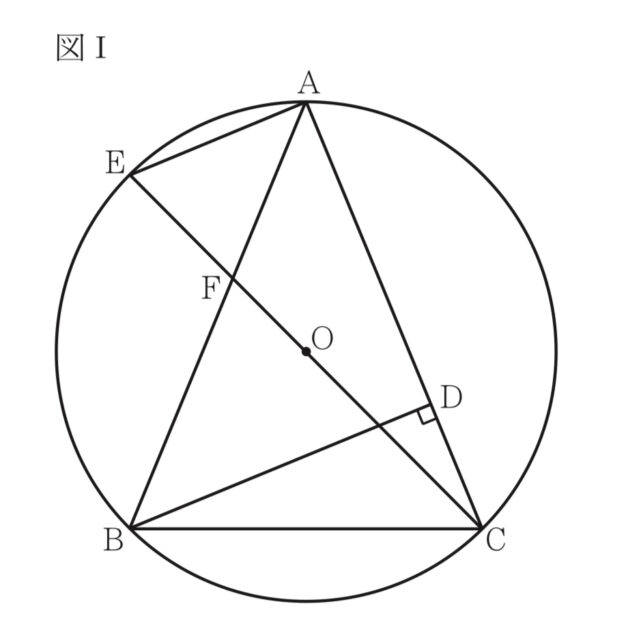
4-1:△EAC△CDBであることを証明しなさい

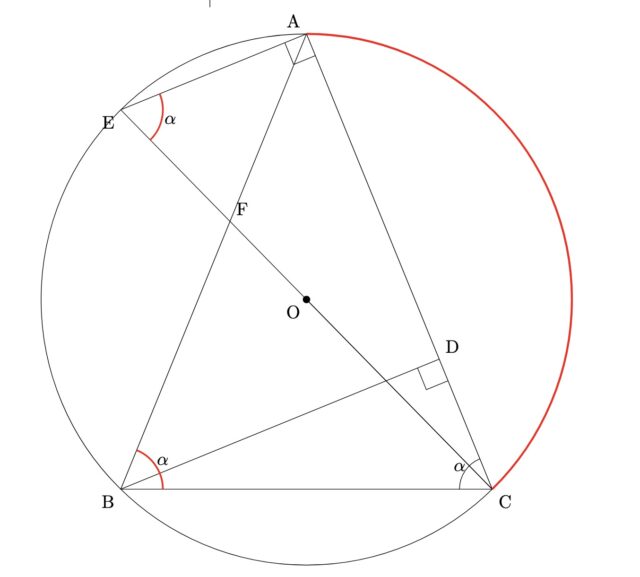
解説 ： △EACと△CDBにおいて、仮定より∠CDB=90°, ∠EACは直径に対する円周角より90°。よって∠EAC=∠CDB=90°⋯①. また、弧ACに対する円周角より∠AEC=∠ABC(=α), △ABCはAB=ACの二等辺三角形より、∠ABC=∠DCB(=α)。したがって、∠AEC=∠DCB⋯②. ①、②より△AECと△CDBは二角相等、△EAC∽△CDBである

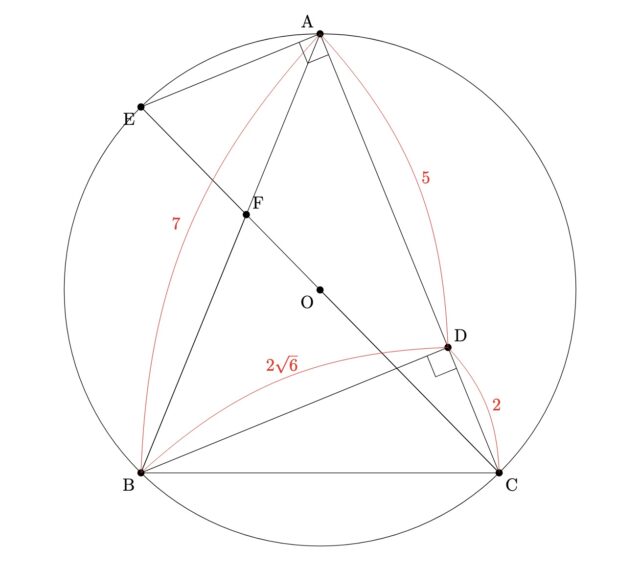
AD5cm、DC=2cmであるとき

4-2①: 線分 BDの長さを求めなさい

解答 ： 2√6

解説 ： AB=AC=AD+DC=5+2=7で, △ADBにおいて三平方の定理よりBD^2=AB^2-AD^2, BD^2=7^2-5^2, BD^2=24, BD=√24=2√6(BD>0)

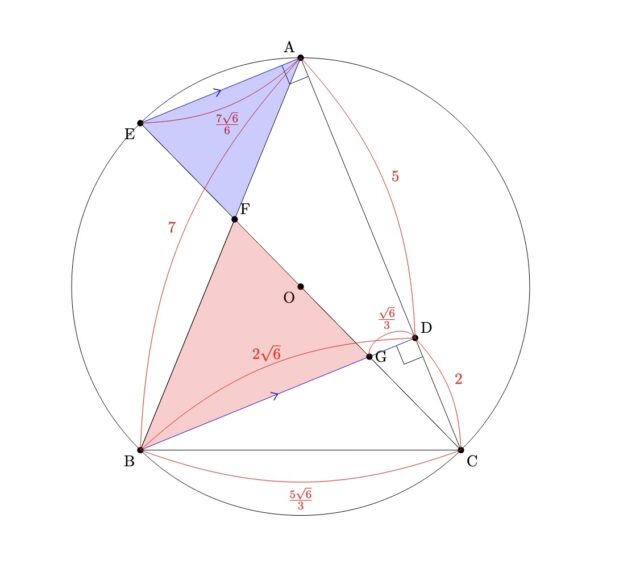
4-2②:線分AFの長さを求めなさい

解答 ： 49/17

解説 ： ①よりBD=2√6, △BCDで三平方の定理よりBC^2=BD^2+CD^2, BC^2=(2√6)^2+2^2=28, BC=2√7(BC>0). (1)より△EAC∽△CDBで、相似比はAC:DBから7:2√6. よってAEはAE:DC=7:2√6, AE:2=7:2√6, AE=(7√6)/6. ここで、辺ECと辺BDの交点をGとする。∠EAC=∠CDB=90°より、同位角は等しく、AE//BD. ∠EAC=∠CDB, ∠ACE=∠DCG(共通な角)より二角相等で△CAE∽CDG. 相似比はCD:CAから2:7. GD:AE=2:7, GD:(7√6)/6=2:7, GD=√6/3. BDは2√6だったので、GB=2√6-√6/3=(5√6)/3. さらに、AE//BDから錯角は等しく、∠EAF=BGF, 対頂角は等しく∠AFE=∠GFB. よって二角相等で△AEF∽△GBF. 相似比はAE:GBより(7√6)/6:(5√6)/3. AF=yとするとFB=AB-AF=7-yとなり、AF:FB=(7√6)/6:(5√6)/3, y:(7-y)=(7√6)/6:(5√6)/3, {(5√6)/3}y={(7√6)/6}×(7-y), 17y/10=49/10, y=49/17

【Ⅱ】 図Ⅱにおいて、立体A-BCDEは四角すい であり、直線ABは平面BCDEと垂直である。 AB=3cである。四角形BCDEは長方形で あり、 BC=5cmN BE=4cである。Fは、 辺AE上の点である。Gは、Fを通り辺DEに 平行な直線と辺ADとの交点である。GとE とを結ぶ。Hは、Gを通り辺CDに平行な直線 と辺ACとの交点である。HとBとを結ぶ。 このとき、4点H、G、E、Bは同じ平面上にある。 次の問いに答えなさい

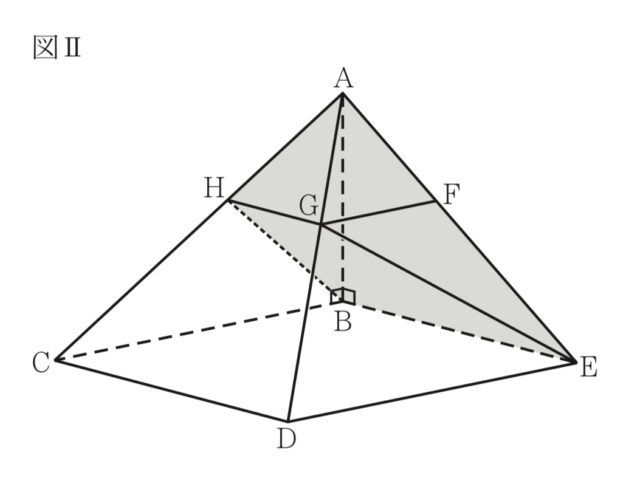
4-3:次のア~エの角のうち、その大きさが90°であるものはどれですか。すべて選び、記号を○で 囲みなさい。 ア △ACDの内角∠ACD イ △ACDの内角∠ADC ウ △ADEの内角∠ADE エ △ADEの内角∠AED

解答 ： ア, エ

解説 ： 直線ABは平面BCDEと垂直より、上から見れば、辺BCと辺ACは重なっており、∠BCD=90°より∠ACDも同じく90°。同様に∠AEDも90°

E=3c cmであるとき

4-4①: △HCBの面積を求めなさい

解答 ： 9/2

解説 ： HからCBへの垂線を引き、CBとの交点をIとする。同様にFからBEへの垂線とその交点をJとする。HG//CD, GF//DEよりHI=FJ。よってFJを求めていく。△ABEと△FJEは∠ABE=∠FJE=90°, ∠AEB=∠FEJの二角相等で相似。また、△ABEで三平方の定理より、AE=√(AB^2+BE^2)=√(3^2+4^2)=5(AC>0)で、問題文よりFE=3. よって△ABEと△FJEの相似比は5:3. 5:3=AB:FJ, 5:3=3:FJ, FJ=9/5. よってHI=9/5. CB=5だったので、△HCBの面積は1/2×9/5×5=9/2.

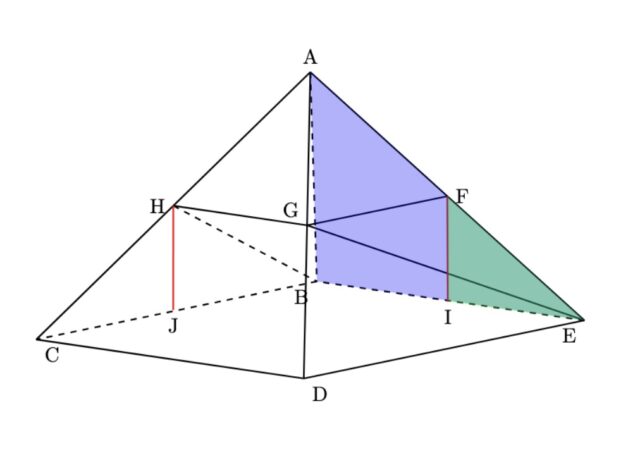
4-4②:立体 AHGEBの体積を求めなさい。

解答 ： 28/5

解説 ： 立体AHGEBを三角錐G-ABHと三角錐G-ABEに分けて考える。(3)より∠ACDと∠AEDは90°, HG//CD, GF//DEより辺GHは面AHBに垂直で辺GFは面ABEに垂直。(4)①よりAF:FE=AH:HC=2:5なので、HG:CD=2:5, HG:4=2:5, HG=8/5. 同様にGF:DE=2:5, GF:5=2:5, GF=2. △AHB=△ABC-△HCB=(1/2×3×5)-9/2=3, △ABE=1/2×3×4=6. 以上より、立体AHGEB=三角錐G-ABH+三角錐G-ABE=(1/3×8/5×3)+(1/3×2×6)=8/5+4=28/5.