2025年度大阪学力検査問題過去問【数学C】

■問題PDF　

■目次　

■大問１

次の問いに答えなさい。

1-1:x=2−√2のとき、x^2−4x+6 の値を求めなさい。

解答 ： 4

解説 ： x^2−4x+6=(x-2)^2+2, これにx=2−√2を代入して計算。{2-√(2)-2}^2+2=4

1-2:(3x+y) ^2−3x−y−2 を因数分解しなさい。

解答 ： (3x+y-2)(3x+y+1)

解説 ： A=3x+yとおくと、式はA^2−A−2となる。因数分解するとA^2−A−2=(A−2)(A+1)。元の式に戻し、(3x+y−2)(3x+y+1)

1-3:a、bを定数とする。x、yの連立方程式
x+ay=4−2b
bx+y=2a
​の解が x=5、y=−1であるとき, a、bの値をそれぞれ求めなさい。

解答 ： aの値7, bの値3

解説 ： x+ay=4−2b に x=5, y=−1 を代入し、5+a(−1)=4−2b, 5−a=4−2b, a-2b=1⋯①
次に、bx+y=2a に代入し、5b−1=2a⋯②
①より a=1+2b を②に代入：5b−1=2(1+2b), 5b−1=2+4b, b=3, また、a=1+2×3=7

1-4:n を自然数とする 2√n<√x<3√nを満たす自然数 x の個数を n を用いて表しなさい

解答 ： 5n-1

解説 ： 2√n<√x<3√n を両辺2乗すると4n

1-5:a、b を定数とし、a

解答 ： aの値-6, bの値1

解説 ： 関数 y=(1/2)x^2は原点を頂点とする下に凸の放物線であり, yの変域が0から始まるため、xの変域は0を含む。条件①より、xの変域は0を含み、最大値が18. よって36=(1/2)x^2, x^2=36, x=±6. したがって、a≤0≤b であり、|a|=6 または |b|=6 となる。条件②より、c≤0≤dであり、最大値が8。8=(1/2)x^2, x^2=16, x=±4. したがって、|c|=4 または |d|=4 となる。c=a+3,d=b+3 の関係から、a≤−3 かつ b≥−3。これらの条件をすべて満たすのは、a=−6。このとき、c=a+3=−6+3=−3。条件②の最大値から、d が正の値となり d=4。b+3=4, b=1。a=−6,b=1の組み合わせはすべての条件を満たす。

1-6:A、B二つのさいころを同時に投げ、Aのさいころの出る目の数を a、Bのさいころの出る目の数を b とし、c=2a+b とする。このとき、2025/cの値が自然数である確率はいくらですか。1から6までのどの目が出ることも同様に確からしいものとして答えなさい。

解答 ： 2/9

解説 ： 2025の約数の中から、c=2a+b(2≤c≤18)となるものを調べる。2025=3^4×5^2より、約数は：1,3,5,9,15,27,45,75,135,225,405,675,2025 このうち、c=2a+bがなり得るのは：3, 5, 9, 15
2a+b=3, (a=1,b=1)
2a+b=5, (a=1,b=3), (a=2,b=1)
2a+b=9, (a=2,b=5), (a=3,b=3), (a=4,b=1)
2a+b=15, (a=5,b=5), (a=6,b=3)
よって(1,1), (1,3), (2,1), (2,5), (3,3), (4,1), (4,7), (5,5), (6,3)の8通り。全体は6×6=36通り。確率は 8/36=2/9

1-7:n を2けたの自然数とする。次の二つの条件を同時に満たす n の値をすべて求めなさい。 ・n の一の位の数は、n^2の一の位の数と同じである。 ・n の十の位の数は、70n の十の位の数より3大きい。

解答 ： 30, 56, 85

解説 ： n=10a+b とおく（aが十の位、bが一の位、1≤a≤9, 0≤b≤9）
条件①：nの一の位 = n^2の一の位
この条件を満たすbは：0,1,5,6
条件②：a = 70nの十の位 + 3
70n=70(10a+b)=700a+70b, すなわち70nの十の位は70bの十の位に等しい。よって
b=0のとき, 70nの十の位は0, よってa=3→n=30
b=1のとき, 70nの十の位は7, よってa=10. 1≤a≤9より不適
b=5のとき, 70nの十の位は5, よってa=8→n=85
b=6のとき, 70nの十の位は2, よってa=5→n=56

1-8:右の図において、m は関数 y=ax^2(a は正の定数)のグラフを表す。四角形ABCDは平行四辺形であり、A、B、Dは m 上にある。辺ADは y 軸に平行であって、Aの x 座標は-3であり、Bの x 座標は-1である。Eは、辺ADと y 軸との交点である。EとCとを結ぶ。ℓ は、Cを通り傾きが1/2の直線である。Fはl上の点であり、Fの x 座標はAの x 座標と等しい。EとFとを結ぶ。四角形ABCDの面積と△EFCの面積は等しい。a の値を求めなさい。答えを求める過程がわかるように、途中の式を含めた求め方も説明すること。ただし、原点Oから点 (1,0) までの距離、原点Oから点 (0,1) までの距離はそれぞれ1cmであるとする。

解説 ： A, B, C, Dそれぞれの座標をaを使って払わすと、A(-3, 9a), B(-1, a), C(5, a), D(3, 9a)となる。直線lの切片をaを使って表すとy=(1/2)x+a-5/2. 平行四辺形ABCDの面積は6×8a=48a. 一方、△EFCの面積は、直線lとy軸との交点をGとするとG(0, a-5/2)であることから、EG=9a-(a-5/2)=8a+5/2. よって△EFC=△EFG+△CEG=1/2(8a+5/2)×3+1/2(8a+5/2)×5=32a+10. この2つの面積が等しいことから、48a=32a+10, a=5/8.

---

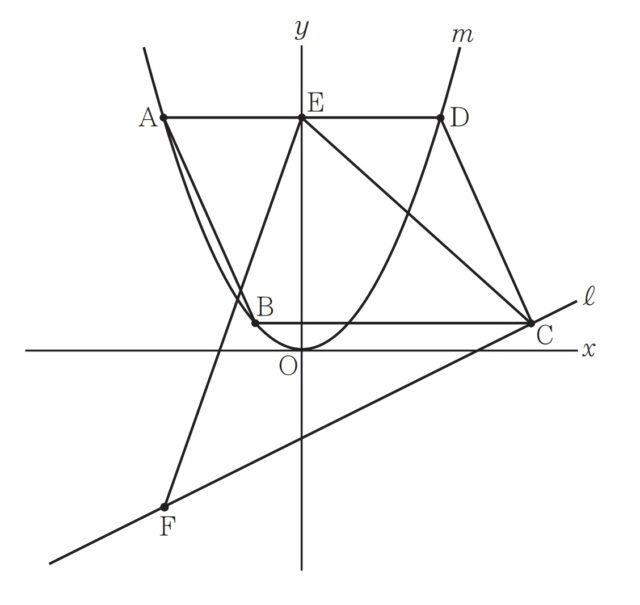
■大問２

---

右の図において、△ABCはAB=ACの二等辺三角形である。Dは、△ABCの頂角∠BACの二等分線と辺BCとの交点である。E、Fは辺AB上にあってA、Bと異なる点であり、AE=EF=FBである。CとEとを結ぶ。Gは、線分ECと線分ADとの交点である。Hは、Aから直線FDにひいた垂線と直線FDとの交点である。Hは、直線ABについてCと反対側にある。HとBとを結ぶ。次の問いに答えなさい。

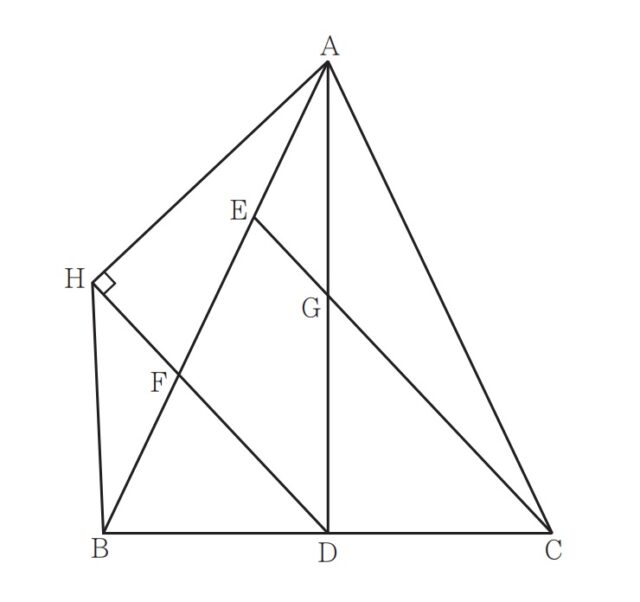
2-1:△ABCの内角∠BACの大きさを x とするどき、△ABCの頂点Cにおける外角の大きさを x を用いて表しなさい。

解答 ： (1/2)a+90

解説 ： 三角形の内角の和が180°であることから、∠BAC +∠ABC +∠ACB = 180°. △ABCは二等辺三角形より底角は等しく、∠ABC=∠ACB. よってa + 2∠ACB = 180°, ∠ACB = (180−a)/2 = 90−a/2. 頂点Cにおける外角は、内角∠ACBの補角より180−∠ACB = 180−(90−a/2) = 90+a/2

2-2:△AHD∽△CDGであることを証明しなさい。

解説 ： △ABCはAB=ACの二等辺三角形であり、ADは頂角∠BACの二等分線である。二等辺三角形の頂角の二等分線は、底辺を垂直に二等分するため、ADはBCの垂直二等分線となる。よって∠AHD=∠CDG=90°⋯① また、BD=DCであり、仮定からBF=FE、よって中点連結定理より、CE//DF。平行線の錯覚は等しく、∠ADH=∠CGD⋯② ①、②より二角相等で△AHD∽△CDG

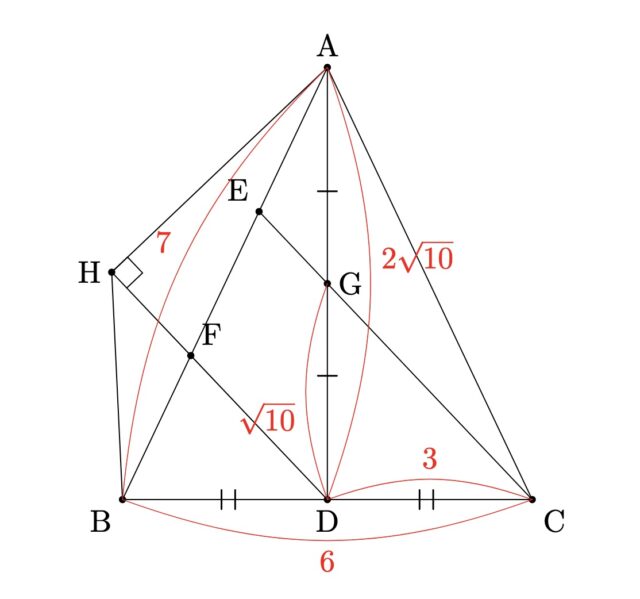
AB=7cm、BC=6cmであるとき、

2-3①:線分GCの長さを求めなさい。

解答 ： √19

解説 ： AB=AC=7cm、BC=6cm である。ADはBCの垂直二等分線より、DはBCの中点であり、CD=3。△ADCは直角三角形で、三平方の定理より：AD^2+CD^2 =AC^2, AD^2+3^2=7^2, AD=√40=2√10(AD>0). 2の証明よりCE//DF、△AFDで中点連結定理よりGはADの中点。よってGD=√10。△CDGに三平方の定理を使いGC^2=CD^2+GD^2=3^2+(√10)^2=19, GC =√19

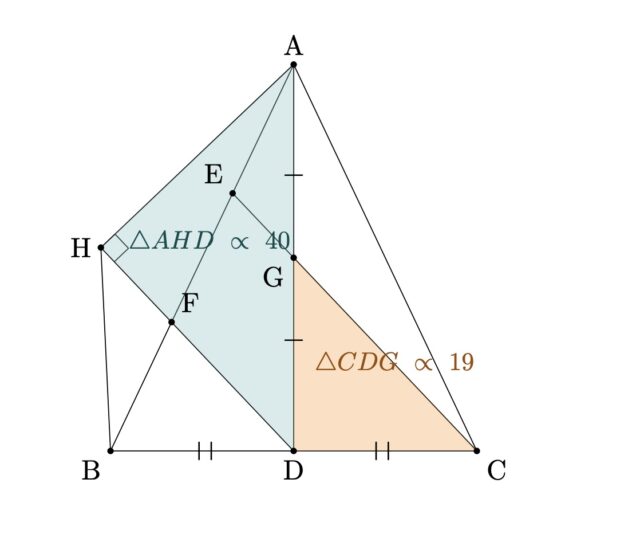
2-3②:△AHBの面積を求めなさい。

解答 ： {33√(10)}/19

解説 ： △AHD∽△CDGと(3)①より、△AHDと△CDGの面積比は40:19とわかる。また、△AGCもAG:GD=1:1より、同じように19と表せる。よって、△ADCは38、同様に△ABDも38となる。また、AE=EF=FBより、△AFDと△ABDの面積比は3:2. したがって、△AFDは76/3となる。△AHF=△AHD-△AFDより、44/3. また、AF:FB=2:1より、△HFB＝22/3となる。以上より、△AHB=66/3=22となり、△CGDを19としていたので、面積比から面積を考え、△AHB=△CGD×22/19=(1/2)×√(10)×3×22/19={33√(10)}/19

---

■大問３

---

図1、図Ⅱにおいて、立体 ABCDEFは五つの平面で囲まれてできた立体である。△DEFは∠DFE=90°の直角三角形であり、DF=5cm、EF=4cmである。四角形BEFCは長方形であり、BE=3cmである。四角形CFDAはCF // ADの台形であり、∠CFD=∠ADF=90°。AD=6cmである。四角形BEDAはBE//ADの台形であり、∠BED=∠ADE=90°である。このとき、△ABCは∠ACB=90°の直角三角形である。次の問いに答えなさい。

3-1:図1において、四角形GHLJは長方形であり、G、H、I、Jはそれぞれ辺AB、DE、DF、AC上にある。このとき、GH//BE、GJ//BCである。Kは、Iを通り辺ACに平行な直線と辺ADとの交点である。

3-1①: 次のア~オのうち、辺ABとねじれの位置にある辺はどれですか。すべて選び、記号を⚪︎で囲みなさい。 ア 辺AD イ 辺DF ウ 辺DE エ 辺EF オ 辺CF

解答 ： イ, エ, オ

解説 ： 並行でなく交わらない直線を選ぶ。

3-1②:△AGJの面積は△KIDの面積の何倍であるか求めなさい。

解答 ： {4√(34)}/15

解説 ： GJ＝xとする。BC=4より、△AGJ:△ABC=x:4となる。CからADへFDと並行に垂線を下ろし、その交点をLとすると、△ACLはAD=6とCF=3から、AL=3でFD=5からCL=5。よって、三平方の定理よりAC=√(34). よって、AJ:AC=x:x+4より、AJ={√(34)x}/4. また、GJ＝HIよりHI=x、CL=5よりFD=5、EF=4で△DHI:△DEF=x:4なので、DI:DF=x:x+4, DI:5=x:x=4, DI=5x/4. △CLA∽△IDKで、CL:ID=5:5x/4より、AL:KD=5:5x/4, 3:KD=5:5x/4, KD=3x/4. 以上より、△AGJ=1/2×(x)×{√(34)x}/4={√(34)x^2}/8, △KID=1/2×5x/4×3x/4=15x^2/32. よって、[{√(34)x^2}/8]÷[15x^2/32]={4√(34)}/15

3-1③:辺GIの長さが辺GJの長さより1cm長いときの四角形GHIJの周の長さを求めなさい。

解答 ： 94/7

解説 ： ②より、GJ=xよすると、JI=x+1. また、AD=6とKD=3x/4より、AK=6-3x/4. また、条件よりAJIKは平行四辺形なので、AK＝JIよって6-3x/4=x+1, x=20/7. 以上よりJI=20/7+1=27/7. よって、四角形GHIJの周の長さは、2(20/7+27/7)=94/7

図Ⅱにおいて、Lは辺DF上にあって、線分ALの長さと線分LEの長さとの和が最も小さくなる点である。LとCとを結ぶ。Mは、Lを通り辺EFに平行な直線と辺DEとの交点である。MとA、MとBとをそれぞれ結ぶ。

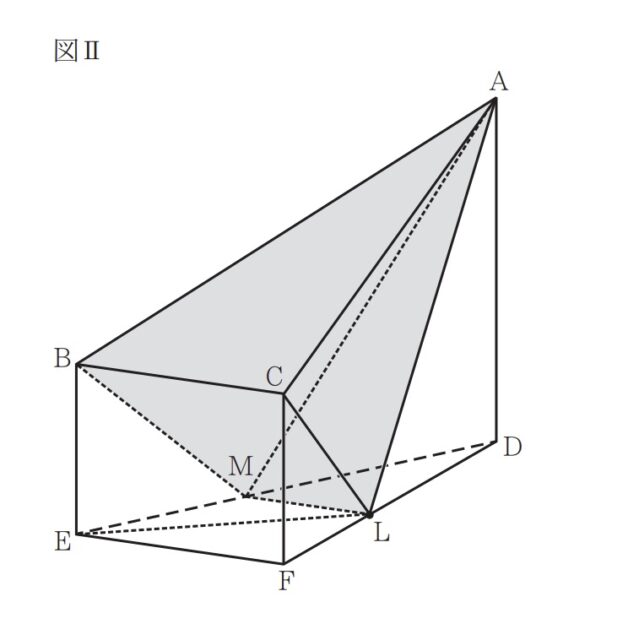
3-2①:線分MLの長さを求めなさい。

解答 ： 12/5

解説 ： CFの延長線上にEF=E_pFとなるような点をE_pとし、Dと結ぶ。LはALとLEの長さが最小になるようになる点なので新しく定義した点E_pとも交わるように直線ALを伸ばすことができる。よって、CFとADは並行だったので、△ALDと△E_pLFは相似。また、その相似比はAD＝6、EF=E_pF=4より3:2。FD=5より、DL=3, FL=2. ここで、△DEFと△DMLの相似を考え、DL:DF=ML:EF, 3:5=ML:4, ML=12/5

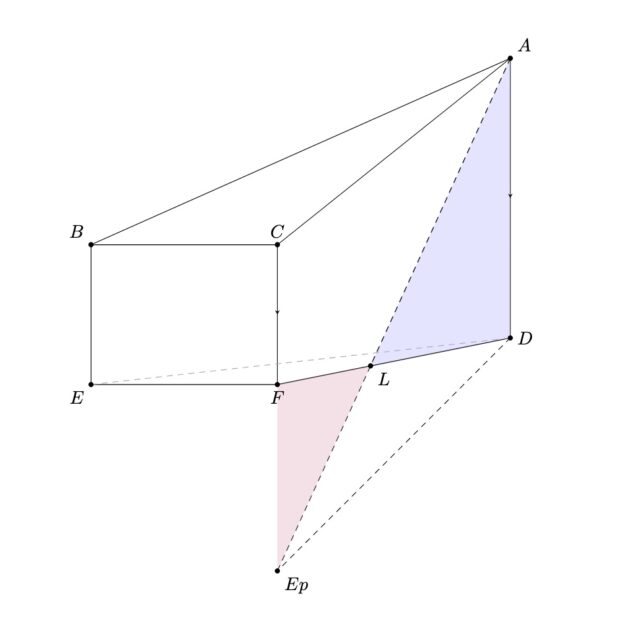
3-2②:立体ABMLCの体積を求めなさい。

解答 ： 112/5

解説 ： 立体全体の体積から立体BCEFMLと立体ADMLを引いたものを考える。まず、全体の体積は△EFDを底面として考え、高さはBE, CF,ADの平均を取り、(3+3+6)/3=4. よって1/2×4×5×4=40. 立体BCEFMLも同様に△CFLを底面とし、高さはBC, EF, MLの平均を取り、(4+4+12/5)/3=52/15. よって1/2×2×3×52/15=52/5. 最後に立体ADMLは底面をMLD、高さをADとする三角錐なので、体積は1/2×12/5×3×6×1/3=36/5となる。以上より、立体ABMLC=40-52/5-36/5=112/5.