2025年度滋賀学力検査問題過去問【数学】

■問題PDF　

■目次　

■大問１

次の1から9までの各問いに答えなさい。

1-1:−3×(−2)−5 を計算しなさい。

解答 ： 1

解説 ： ※かけ算から計算しましょう。
-3×(-2)-5=6-5=1

1-2:[3/5]a-[2/3]a を計算しなさい。

解答 ： -[1/15]a

解説 ： ※通分して解きます。
[3/5]a-[2/3]a=[9/15]a-[10/15]a=-[1/15]a

1-3:次の等式を [ ]内の文字について解きなさい。
a=1/2 (x+y) [y]

解答 ： y=2a-x

解説 ： まず、両辺に2をかけて分数をなくします。
2a=x+y
次に、y を求めるために、両辺から x を引きます。
2a−x=y
したがって、y について解くと、以下のようになります。
y=2a−x

1-4:次の連立方程式を解きなさい。
y=2x+4
3x+2y=1

解答 ： x=-1,y=2

解説 ： ★代入法を使用します。
y=2x+4⋯(1)
3x+2y=1⋯(2)
方程式(1)の y を方程式(2)に代入します。
3x+2(2x+4)=1
3x+4x+8=1
7x+8=1
7x=1−8
7x=−7
x=−1

x=-1を⑴に代入します。
y=2×-1+4=-2+4=2

1-5:次の2次方程式を解きなさい。
x²+2x−24=0

解答 ： x=-6,4

解説 ： ★因数分解を使って解きます。
x²＋2x-24=0
(x−4)(x+6)=0
x=4,-6

1-6: (3√2+2)(√2−2) を計算しなさい。

解答 ： 2-4√2

解説 ： (3√2+2)(√2−2)=3√2×√2+3√2×-2+2×√2+2×-2=6-6√2+2√2-4=2-4√2

1-7:下の図は、底面の半径が3、母線の長さが5の円すいです。この円すいの側面積を求めなさい。

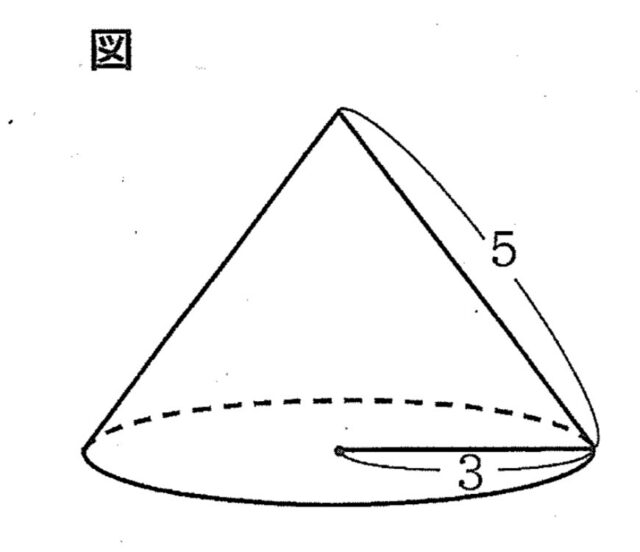
解答 ： 15π

解説 ： 円すいの側面積を求めるには、以下の公式を使います。
側面積=母線の長さ×底面の半径×π
・底面の半径 (r) = 3
・母線の長さ (l) = 5
これらの値を公式に当てはめます。
5×3×π=15π

1-8:右の図のように、関数 y=12/xのx>0の部分のグラフがあります。大小2つのさいころを同時に1回投げ、大きいさいころの出た目の数をa, 小さいさいころの出た目の数をbとし、x座標がa,y座標がbの点Aを考えるとき、点Aがこのグラフ上にある確率を求めなさい。
ただし、大小2つのさいころはともに、1から6までのどの目が出ることも同様に確からしいとします。

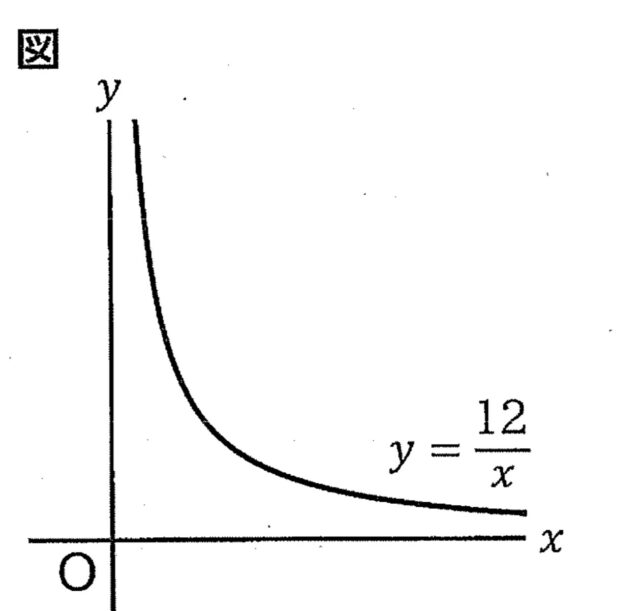
解答 ： 1/9

解説 ： 大小2つのサイコロを同時に1回投げるので、出た目の組み合わせの総数は 6×6=36 通りです。
点Aがグラフ上にあるということは、点Aの座標 (a,b) が関数 y=12/xの式を満たすということです。つまり、b=12/aという関係が成り立ちます。
a と b はサイコロの目なので、どちらも1から6までの整数です。この条件を満たす (a,b) の組み合わせを探します。
・a=1 のとき: b=12。 これはサイコロの目ではないので不適。
・a=2 のとき: b=12/2=6。 組み合わせは (2,6)。
・a=3 のとき: b=12/3=4。 組み合わせは (3,4)。
・a=4 のとき: b=12/4=3。 組み合わせは (4,3)。
・a=5 のとき: b=12/5。 これは整数ではないので不適。
・a=6 のとき: b=12/6=2。 組み合わせは (6,2)。

条件を満たす組み合わせは、(2,6),(3,4),(4,3),(6,2) の4通りです。

確率= 条件を満たす場合の数/すべての起こりうる場合の数=4/36=1/9

1-9:下の図は、あるクラスの25人のハンドボール投げの記録をヒストグラムに表したものです。例えば、記録が10m以上14m未満の人は3人いたことがわかります。この25人の記録の最頻値を求めなさい。また、中央値をふくむ階級を答えなさい。

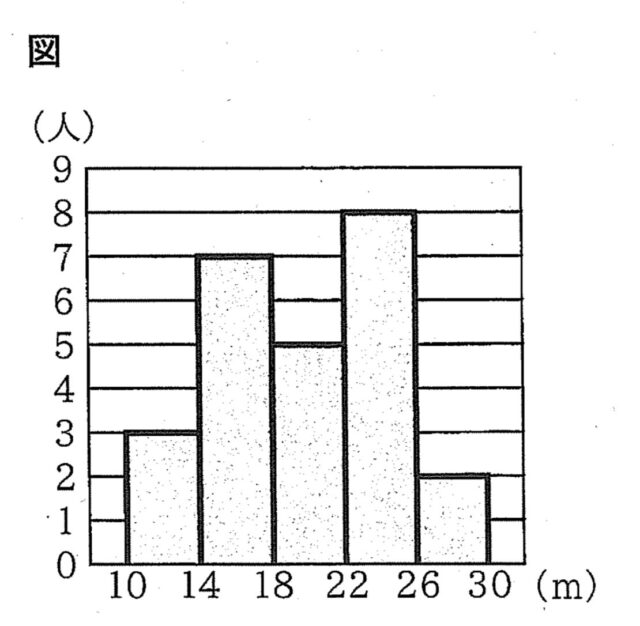
解答 ： 最頻値：24m
階級：18m以上22m未満

解説 ： 最頻値
最頻値とは、度数が最も多い階級の値のことです。
ヒストグラムのグラフを見ると、最も柱が高いのは、記録が22m以上26m未満の階級で、その度数は8人です。したがって、この階級が最頻階級となります。よって、最頻値は(22+26)÷2=24m
中央値
中央値とは、データを大きさの順に並べたとき、ちょうど真ん中にくる値のことです。
このクラスの人数は25人なので、中央値は小さい方から数えて13番目の人の記録になります。
・10m以上14m未満: 3人
・14m以上18m未満: 3 + 7 = 10人
・18m以上22m未満: 10 + 5 = 15人
・22m以上26m未満: 15 + 8 = 23人
・26m以上30m未満: 23 + 2 = 25人
したがって、中央値である13番目の人は、累積人数が15人となる18m以上22m未満の階級に含まれます。

■大問２

いろいろな平面図形について考えます。次の1から3までの各問いに答えなさい。

2-1:図1は、周の長さが54cm, 辺ADの長さが辺ABの長さの2倍の長方形です。辺ABの長さを求めなさい。

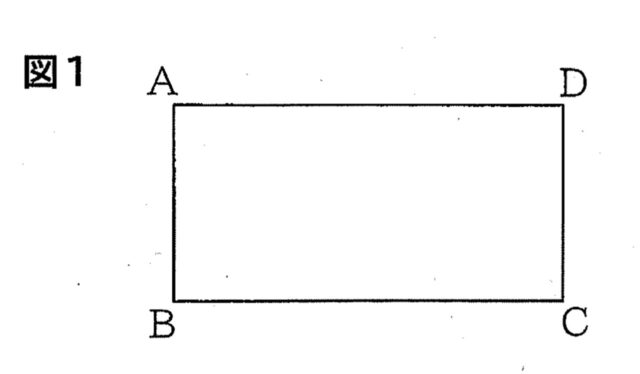
解答 ： 9cm

解説 ： 辺ABの長さを x cmとします。
辺ADの長さは辺ABの2倍なので、2x cmとなります。

長方形の周の長さは、「（縦の長さ + 横の長さ）× 2」で求められます。
したがって、周の長さは (x+2x)×2 という式で表せます。
問題文から、周の長さは54cmなので、次の方程式が成り立ちます。
(x+2x)×2=54
3x×2=54
6x=54
x=54/6
​x=9

2-2:図2のように、直線ℓと2点A, Bがあります。直線ℓは、2点A, Bを通る直線と平行です。このとき、2点A, Bを通り、直線ℓと接する円をコンパスと定規を用いて作図しなさい。ただし、作図に用いた線は消さないこと。

解答 ：

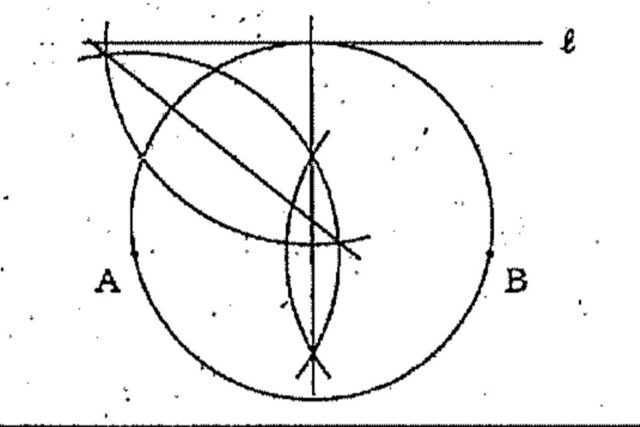
解説 ： ①ABの垂直二等分線を描く。
２点Ａ・Ｂを通る円は、円の中心はＡ・Ｂから等距離にあるということです。つまり、ＡＢの垂直二等分線とℓとの交点が接点なので、ABの垂直二等分線をひきます。
②接点とAの垂直二等分線を描く。
接点も円周上の点となるので、Ａと接点の垂直二等分線をひきます。
③２つの垂直二等分線の交点が円の中心です。この中心から、A,、B、接点の３点を通るように円を描きます。

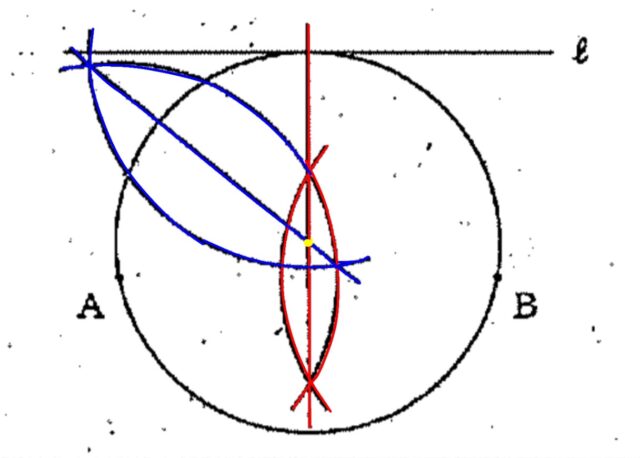
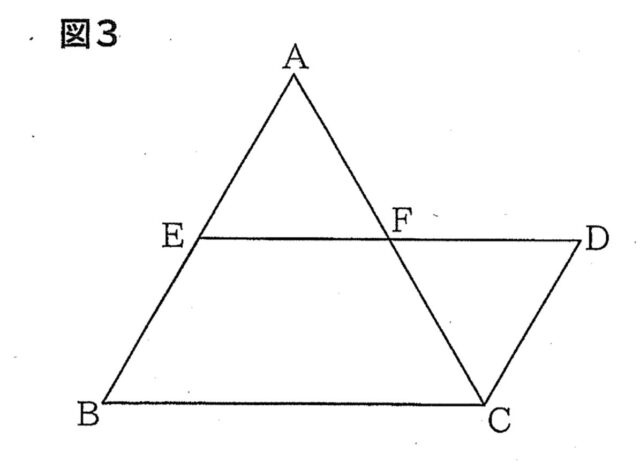
図3のように、正三角形ABCと平行四辺形EBCDがあり、点Eは辺ABの中点です。辺ACとEDの交点をFとするとき、後の①、②の各問いに答えなさい。

2-3①:図4は、図3において、平行四辺形EBCDの対角線の交点をOとし、直線AOと辺ED, BCとの交点をそれぞれP, Qとしたものです。このとき、OP=OQであることを証明しなさい。

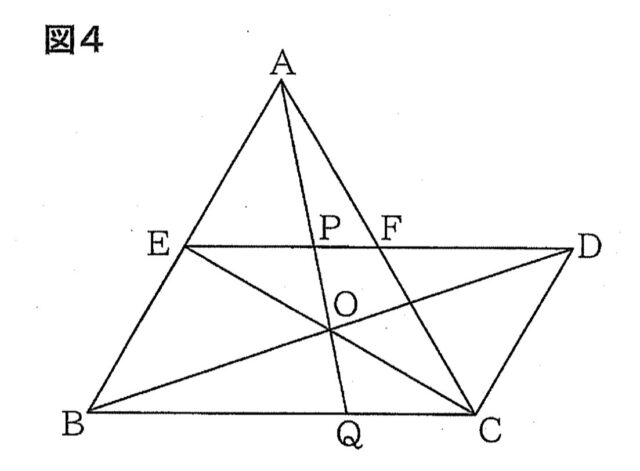
解答 ： 【証明】 △OPEと△OQCで、ED//BCより、平行線の錯角は等しいから ∠OEP=∠OCQ ①。平行四辺形の対角線はそれぞれの中点で交わるから OE=OC ②。対頂角は等しいから ∠POE=∠QOC ③。①, ②, ③から、1組の辺とその両端の角がそれぞれ等しいので、△OPE≡ △OQC。合同な図形の対応する辺は等しいから OP=OQ 。

解説 ： △OPE と △OQC において、
対頂角は等しいので、
∠POE=∠QOC (図4より)
ED // BCより、平行線の錯角は等しいので、
∠OEP=∠OCQ
平行四辺形EBCDの対角線はそれぞれの中点で交わるため、
OE=OC
上記の1組の辺とその両端の角がそれぞれ等しいことから、
△OPE≡△OQC
合同な図形の対応する辺の長さは等しいので、
OP=OQ

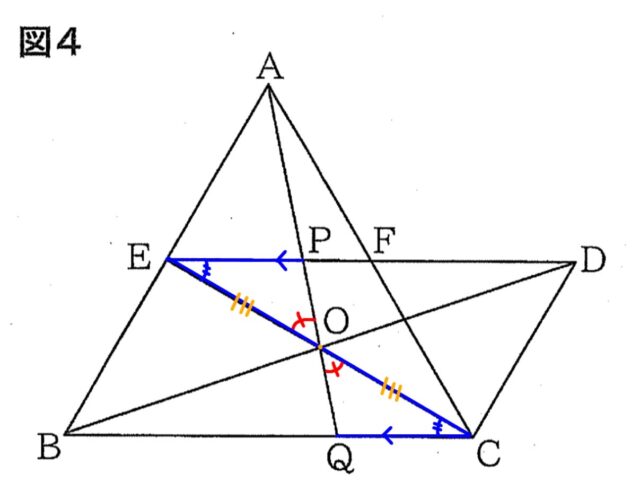
2-3②:図5は、図3において、半直線CD上に△GBCの頂点Gを、△ABCと△GBCの周の長さが等しくなるようにとったものです。このとき、GB: GC=7:3となります。線分BGと辺AC,EDとの交点をそれぞれH, Iとするとき、HI: IGを求めなさい。

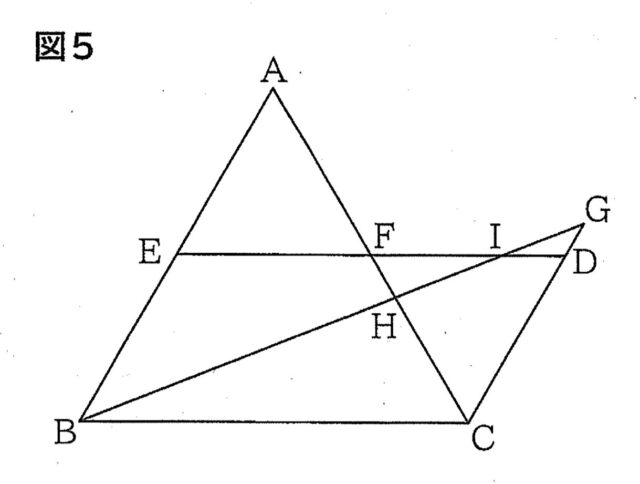
解答 ： HI:IG=5:4

解説 ： 問題文より、GB:GC=7:3であり、△ABCと△GBCの周の長さが等しいので次の式が成り立ちます。
AB+AC+BC=BG+GC+BC
AB+AC=BG+GC
AB+AC=7+3=10
△ABCは正三角形なので、
AB=AC=5
EはABの中点なので、EB=5÷2=2.5
平行四辺形の対辺は等しいので、DC=EB=2.5
GD=GC-DC=3-2.5=0.5

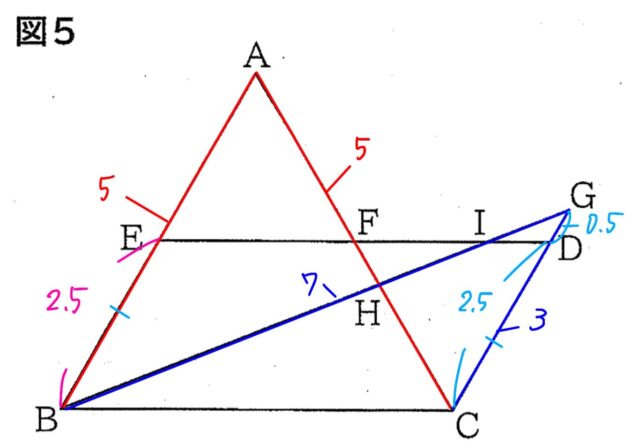
したがって、GD:DC=0.5:2.5=1:5
AE:EB=5:5
△ABH∽△CGHより、BH:HG=AB:GC=10:6=5:3…①
△EBI∽△DGIより、BI:IG=BE:GD=5:1…②


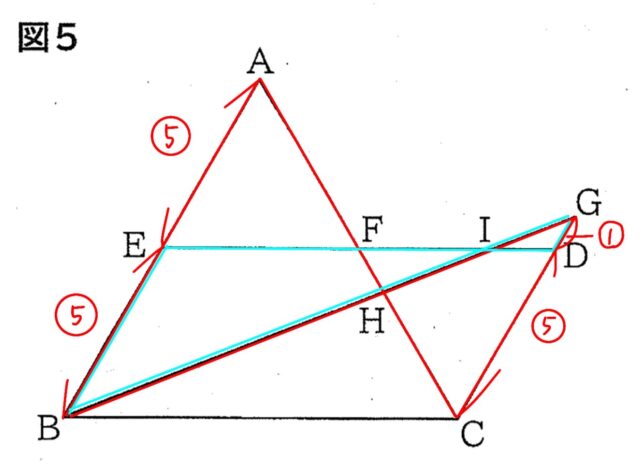
①と②は、比の合計がBG=①:②=5+3:5:1=8:6　となるので、①を3倍、②を４倍して8と6の最小公倍数24で統一すると、
BH:HI:IG=15:5:4
したがって、HI:IG=5:4

■大問３

yがxの2乗に比例する関数について考えます。 図1のように、関数 y=−[1/4]x²のグラフ上に、x座標が4である点Aをとります。このとき、次の1から3までの各問いに答えなさい。

3-1:グラフが、関数 y=−[1/4]x²のグラフと、x軸について対称である関数の式を求めなさい。

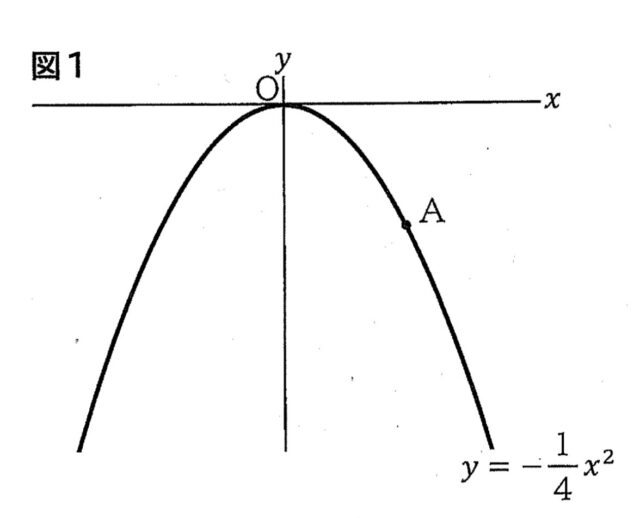
解答 ： y=1/4x²

解説 ： ★yがx軸について対称なグラフは、元のグラフのy座標の符号を逆にしたものです。
元の式が y=−1/4x²なので、yを-yに置き換えます。
−y=−1/4x²
y=1/4x²

3-2:図2は、図1において、関数 y=−1/4x²のグラフ上に、x座標が-6である点Bをとったものです。このとき、2点A, Bの間の距離を求めなさい。

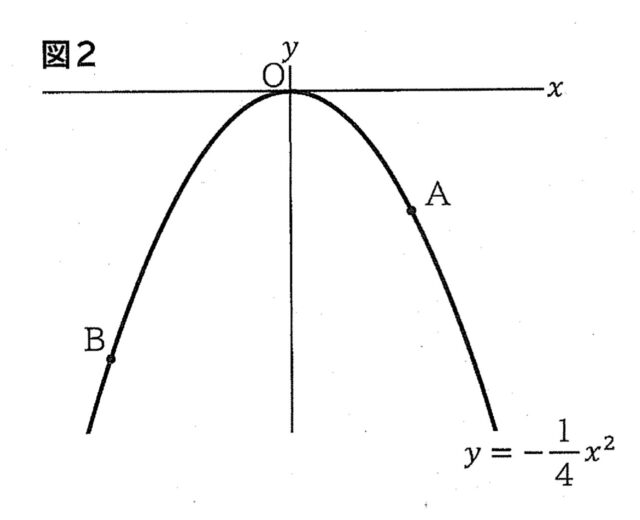
解答 ： 5√5

解説 ： はじめに、点Aと点Bの座標を求めます。
点Aは関数 y=−1/4x²のグラフ上にあり、x座標が4です。
x=4 を式に代入すると、
y=−1/4(4)²=−1/4×16=−4
したがって、点Aの座標は (4,−4) です。
点Bも同じグラフ上にあり、x座標が-6です。
x=−6 を式に代入すると、
y=−1/4(−6)²=−1/4×36=−9
したがって、点Bの座標は (−6,−9) です。



三平方の定理

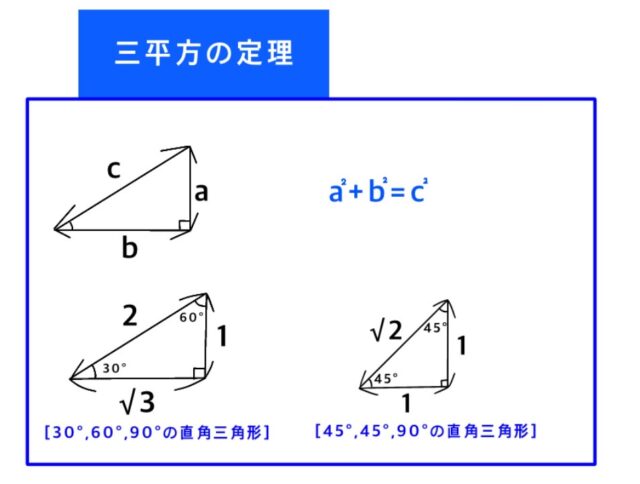
より、
√〔[ −6−4]²+[−9−(−4)]²〕=√[(-10)²+(-5)²]=√[100-25]=√75=5√5

図3は、図1において、関数 y=−1/4x²のグラフ上に、x座標がtである点Pをとったものです。このとき、後の①、②の各問いに答えなさい。
ただし、 0

3-3①:図4は、図3において、点Pを通りy軸に平行な直線ℓと、点Aを通りx軸に平行な直線mとの交点をQとし、点Pを通りx軸に平行な直線nと関数y=-1/4x²のグラフとの交点のうち、点Pと異なる点をRとしたものです。PQ=PRとなるとき、tの値を求めなさい。

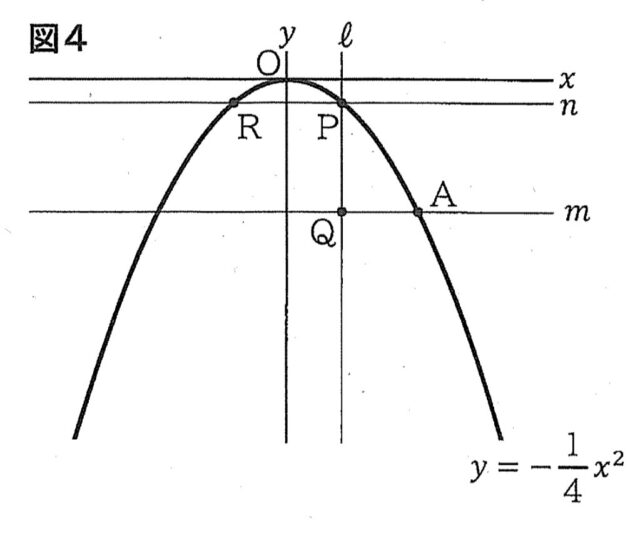
解答 ： t=-4+4√2

解説 ： はじめに、各点の場所（座標）を調べます。
・点P: グラフ y=−1/4x²の上にあり、x座標は t です。y座標は式に x=t を代入して計算します。Pの座標は (t,−1/4t²) です。
・点Q: x座標は点Pと同じなので t です。y座標は点Aと同じなので、まず点Aのy座標を求めます。
点Aのx座標は4なので、式に x=4 を代入すると、y=−1/4(4)²=−4 です。Qの座標は (t,−4) です。
・点R: y座標は点Pと同じなので −1/4t²です。x座標は、y=−1/4x²の式に y=−1/4x²を代入して求めます。
-1/4t²=-1/4x²
t²=x²なので、x=±t となります。
RはPと異なる点なので、Rのx座標は-tです。
Rの座標は (−t,−1/4t²) です。

次に、2つの長さ（PQとPR）をtの式で表します。
・PQの長さ: 点Pと点Qは、縦に並んでいます。長さはy座標の差で計算できるので、
PQ=(点Qのy座標)−(点Pのy座標)
PQ=−4−(−1/4t² )=4−1/4t² 　となります。
・PRの長さ: 点Pと点Rは、横に並んでいます。長さはx座標の差で計算できるので、
PR=(点Pのx座標)−(点Rのx座標)
PR=t−(−t)=2t　となります。

「PQの長さ = PRの長さ」なので、次の式が成り立ちます。
4−1/4t²=2t
16−t²=8t
t²+8t−16=0
解の公式

より、
t= [-8±√8²-4(1)(-16)]/2=−4±4√2
問題文に「0

3-3②:図5は、図3において、関数 y=−1/4x²のグラフ上に、x座標が-2である点Cをとり、点OとA,点OとP,点OとC、点CとA,点CとPをそれぞれ結んだものです。このとき、 △OCP の面積は、 △OCA の面積の何倍か、tを使った式で表しなさい。

解答 ： t²+2t/24倍

解説 ： はじめに各点の座標を求めます。
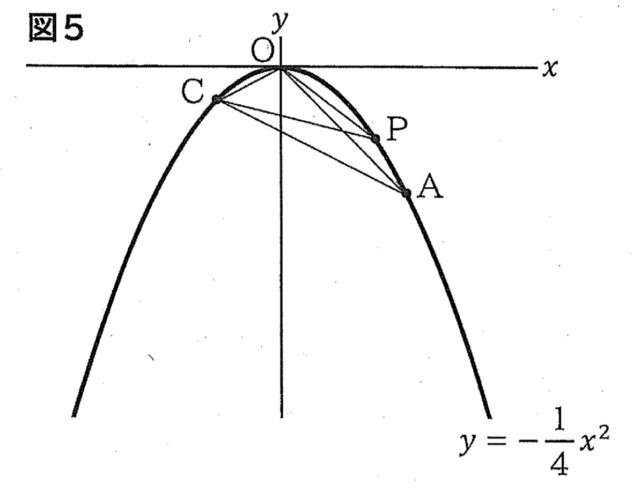
・点O: 原点なので O(0, 0)です。
・点A: グラフ y=−1/4x²上にあり、x座標が4です。
y=−1/4(4)²=−4
なので、A(4, -4)です。
・点C: グラフy=-1/4x²上にあり、x座標が-2です。
y=−1/4(−2)²=−1
なので、C(-2, -1)です。
・点P: グラフy=-1/4x²上にあり、x座標がtです。
y=-1/4t²なので、P(t, -1/4t²)です。

次に、△OCA の面積を求めます。
原点Oと2点A(4, -4),C(-2, -1)を頂点とする三角形の面積を求めます。この面積は、y軸を底辺とする2つの三角形の和として計算できます。
左側の三角形（△OCD’、ただしD’はy軸とACの交点）の面積：底辺はy軸上のDからOまでの長さ、高さは点Cのx座標の絶対値です。
右側の三角形（△OAD’）の面積：底辺はOD’の長さ、高さは点Aのx座標です。
この方法は少し複雑なので、三角形の面積公式を使います。
△OCA の面積 = 1/2I(4)(-1)-(-2)(-4)I=6

次に、△OCP の面積を求めます。
同様に、原点Oと点C(-2, -1),点P(t,1/4t²)の座標を使って面積を求めます。
△OCP の面積 =1/2I(-2)(-1/4t²)-(t)(-1)=1/2I1/2t²+t I
問題の条件より 0 面積は1/2(1/2t²+t)=1/4t²+1/2t=t²+2t/4 となります。

したがって、△OCPの面積が△OCAの面積の何倍かは、
面積(△OCP)/面積(△OCA)=[t²+2t/4]/[6] =[t²+2t]/[4×6]=[t²+2t]/[24]=t(t+2)/24

■大問４

図1のように、奇数が1つずつ書かれたカードを、規則にしたがって並べます。後の1から3までの各問いに答えなさい。

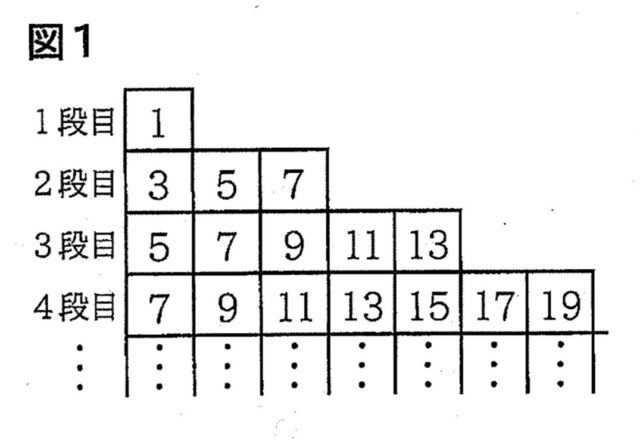【規則】
・各段の左端には、1段目は1, 2段目は3, 3段目は5, …と、段の数を2倍して1をひいた奇数が書かれたカードを並べる。
・各段には、その段の左端のカードに書かれた奇数と同じ枚数のカードを並べる。
・2段目以降は、各段の左端のカードに書かれた奇数から右へ順に、数が2ずつ大きくなるように、カードを並べる。

4-1:10段目の左から3番目のカードに書かれた奇数を答えなさい。

解答 ： 23

解説 ： 規則によると、「段の数を2倍して1をひいた奇数」が各段の左端の数になります。
よって、n段目の左端の数は 2n−1 と表せます。
n=10 を上記の式に代入すると、10段目の左端の数は 2×10−1=19 となります。
規則では、左端の数から右へ順に、数が2ずつ大きくなるので、1番目の数は19です。
2番目の数は 19+2=21 で、3番目の数は 21+2=23 です。
したがって、10段目の左から3番目のカードに書かれた奇数は23です。

4-2:次の説明は、図2のように太線の四角形で囲んだ縦2枚、横2枚の4枚のカードに着目するとき, カードに書かれた4つの奇数には、下線部の性質が成り立つことを、文字を使って説明したものです。ア、イにはnを使った式を、ウには説明の続きを書いて、説明を完成させなさい。
【説明】
自然数nを使って、左上の奇数を2n+1と表すとき、右上の奇数と左下の奇数は[ ア ]、右下の奇数は[ イ ]と表される。
[ ウ ]
したがって、右上の奇数と右下の奇数の積から、左上の奇数と左下の奇数の積をひいた差は、いつも4の倍数になる。

解答 ： ア　2n+3

イ 2n+5

ウ (2n+3)(2n+5) – (2n+1)(2n+3) = 4n² + 10n + 6n + 15 – 4n² – 6n – 2n – 3 = 8n + 12 = 4(2n + 3)。
2n+3は整数だから、4(2n+3)は4の倍数である 。

解説(ア) ： 左上の奇数を 2n+1 とします。
右上の奇数は、同じ段の右隣にあるので、左上の奇数に2を加えた数です。
(2n+1)+2=2n+3

左下の奇数は、左上の奇数が属する段の次の段の、同じ位置にある数です。図1の規則から、各段の左端の数は「段の数を2倍して1をひいた数」です。この規則を当てはめていくと、左下の奇数は右上の奇数と同じになります。
よって、左下の奇数は 2n+3 です。

解説(イ) ： 右下の奇数は、左下の奇数の右隣にあるので、2を加えた数です。
(2n+3)+2=2n+5

解説(ウ) ： ア、イで求めた式を使い、計算式を立てると、
(2n+3)(2n+5)−(2n+1)(2n+3)　となります。これを計算していきます。
4n²+10n+6n+15-(4n²+6n+2n+3)
=4n²+16n+15−4n²−8n−3
=16n−8n15−3
=8n+12
=4(2n+3)
nは自然数なので、2n+3 も整数です。
4に整数をかけた数は、必ず4の倍数になります。
以上のことから、この計算の答えは常に4の倍数になることが証明できます。

4-3:規則にしたがって1段目から順にカードを並べます。このとき、例えば、5が書かれたカードは、2段目の左から2番目にはじめて並び、次に3段目の左端に並びます。図3は、それぞれの奇数のカードがはじめて並ぶときに、色をつけて表したものです。1段目から順にカードを並べていくとき,2025が書かれたカードは、何段目の左から何番目にはじめて並ぶか、答えなさい。

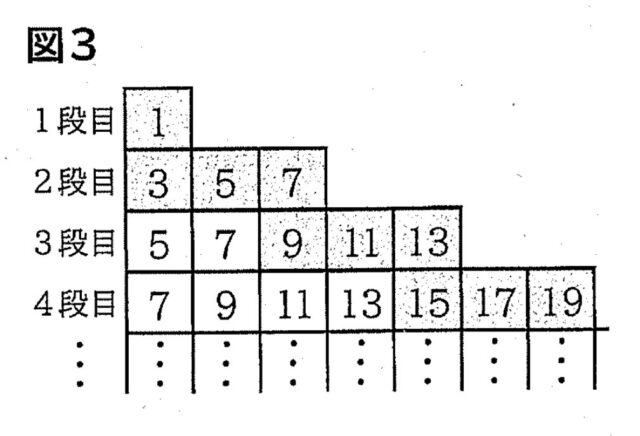
解答 ： 339段目の
左から675番目

解説 ： n段目の左端の数は規則から、段の数を2倍して1をひくので、2n−1 となります。





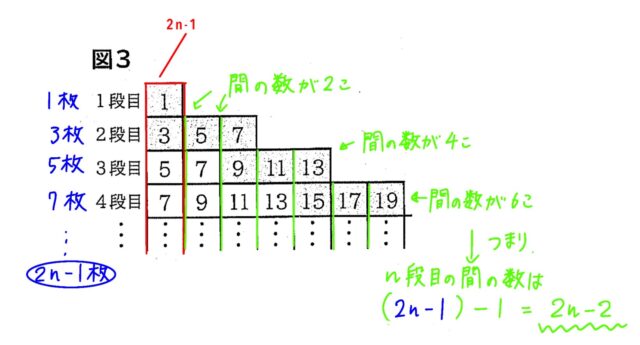
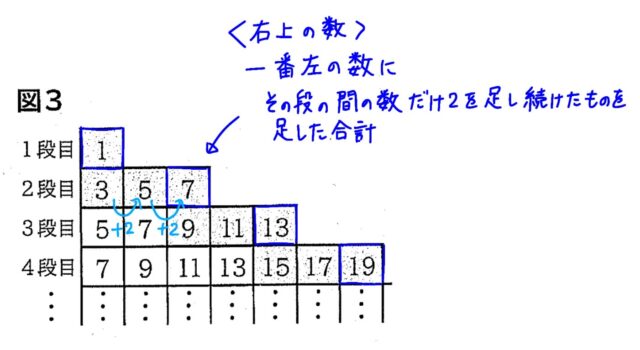
n段目のカードの枚数も左端の数と同じなので、2n−1 枚です。
n段目の右端の数は、左端の数から右に2n−2枚のカードが並んでいるので、2ずつ増える数が2n−2回（間の数）あるので、
(2n−1)+2(2n−2)=2n−1+4n−4=6n−5　です。

2025という奇数がはじめて現れるのは、その前の段の右端の数よりも大きい段なので、n-1段目の右端の数を考えます。



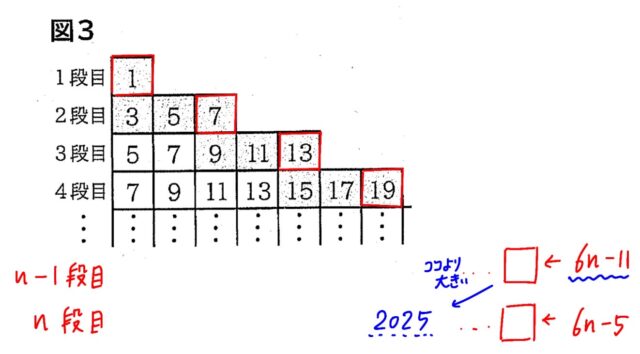
n-1段目の右端の数は、6(n−1)−5=6n−6−5=6n−11 となります。
この数が2025よりも小さくなる、つまり 6n−11<2025 となるnを求めます。
6n<2036
n<339.33...
この計算から、2025という数は、339段目にはじめて並び始めることがわかります。

次に、2025が339段目の左から何番目にあるかを計算します。


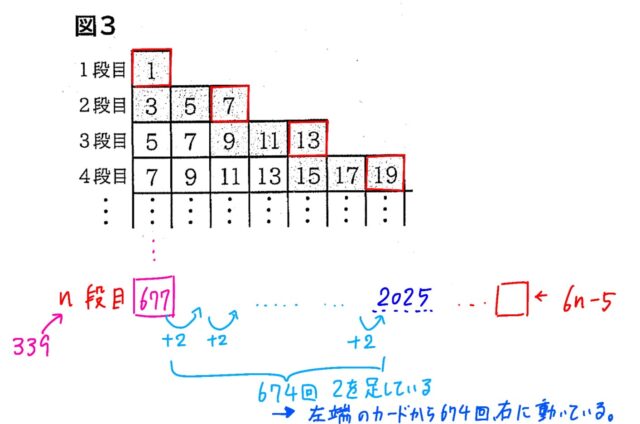
339段目の左端の数は、2n−1の式にn=339を代入して求めます。
2×339−1=678−1=677
2025は左端の数677から始まって、2ずつ増えていきます。つまり、2025にたどり着くまでに何回2を足せばよいかを計算します。
(2025−677)÷2=1348÷2=674
これは、左端のカードから数えて、674回右に移動したことを意味するので、2025は左から数えて 674+1=675 番目になります。