2025年度　広島県公立高校入試問題過去問【数学】

■問題PDF　

■目次　

■大問１

１−１：次の(1)～(8)に答えなさい。

3 + (-8) – (-4)　を計算しなさい。

解答 ： -1

解説 ：
・まずは括弧をとって、式を整える。
3 + (-8) – (-4) = 3 – 8 ₊ 4 = -5 + 4 = -1　よって、答えは　-1。

１−２：2ab² × 5a ÷ b　を計算しなさい。

解答 ： 10a²b

解説 ： 2ab² × 5a ÷ b = 10a²b² ÷ b = 10a²b　よって、答えは　10a²b。

１−３：12/√6 + 3√2 × √3　を計算しなさい。

解答 ： 5√6

解説 ： ・足し算引き算より、掛け算割り算を優先して解く。
・分母に根号が含まれる項は、有理化して計算する。
12/√6 + 3√2 × √3 = 12/√6 + 3√6 = 12 × √6 / √6 × √6 + 3√6 = 12√6 / 6 + 3√6 = 2√6 + 3√6 = 5√6
よって、答えは　5√6。　

１−４：方程式　x² – 16x = 0　を解きなさい。

解答 ： x = 0,　x = -16

解説 ： ・共通因数のxについて、因数分解して解く。

x² – 16x = 0　→　x (x – 16) = 0　→　x = 0，x – 16 = 0　→　x – 16 = 0 より、x = 16
よって、答えは　x = 0，x = 16。

１−５：y は x に比例し、x = -4 のとき y = 8 です。y = -6 のときの x の値を求めなさい。

解答 ： 3

解説 ： 問題文より、yはxに比例するので、y = ax　とおける。
x = -4 のとき y = 8 なので、代入して、8 = a × (-4)　→　8 = -4a　→　4a = -8　→　4a × 1/4 = -8 × 1/4　→　a = -2　これを先においた式に代入して、y = -2x　とわかる。
y = -6 のときのxの値を求めるので、求めた式にy = -6 を代入する。
-6 = -2x　→　2x = 6　→　2x × 1/2 = 6 × 1/2　→　x = 3　よって、答えは　x = 3。

１−６：a を負の数とします。y は x の関数です。このとき、関数 y = a/x について、正しいものを、次のア～エの中から全て選び、その記号を書きなさい。

ア x の変域が x ＞ 0 のとき、x の値が増加すると、y の値は増加する。
イ x の変域が x ＞ 0 のとき、x の値が増加すると、y の値は減少する。
ウ x の変域が x ＜ 0 のとき、x の値が増加すると、y の値は増加する。
エ x の変域が x ＜ 0 のとき、x の値が増加すると、y の値は減少する。

解答 ： ア，ウ

解説 ： 問題文より、y = a/x　は反比例の式だとわかる。加えて、比例定数である a は負の数だとわかっているので、以下のようなグラフだと考えられる。


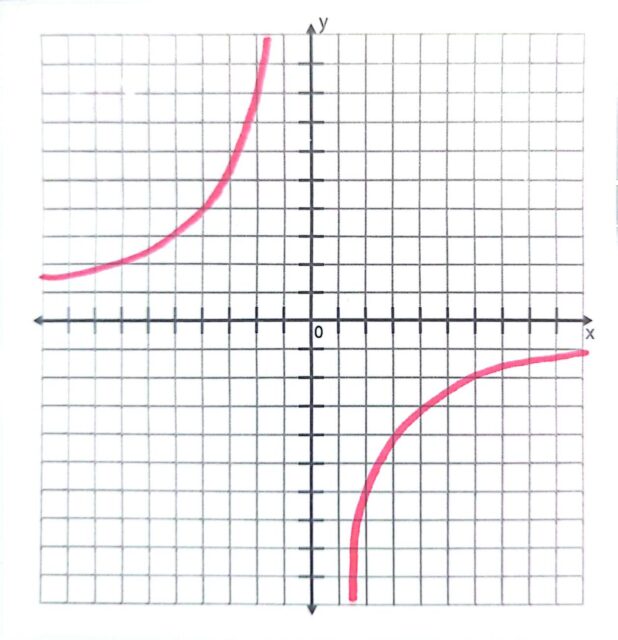
グラフを見ると、xの値が増加するほど(横軸で右にいくほど)、yの値が大きくなることがわかる。
また、xの値が減少するほど(横軸で左にいくほど)、yの値が小さくなることが見て取れる。
したがって、選択肢アとウが適当である。

１−７：右の図のように、AB = 6cm、AD = 3cm の長方形ABCDがあります。長方形ABCDを、辺DCを軸として1回転させてできる立体の体積は何cm³ですか。ただし、円周率は π とします。

解答 ： 54π

解説 ： 長方形ABCDを、辺DCを軸として1回転させてできる立体は以下の図のようになる。

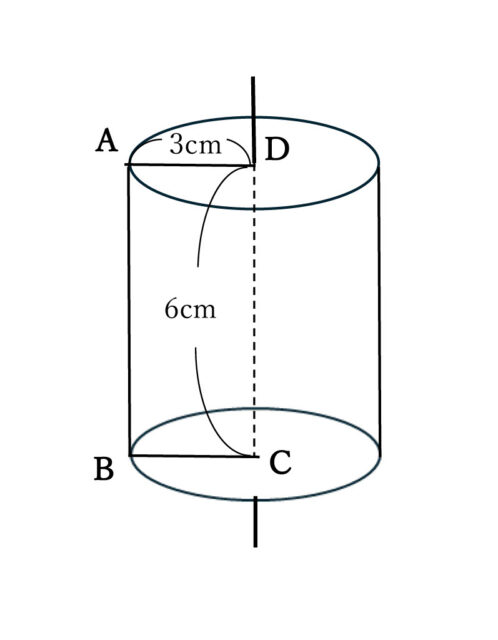
図を見るにこの立体は円柱であり、底面の半径は辺BCや辺ADと等しくなり、3cmだとわかる。同様に、この円柱の高さは辺ABや辺DCの長さと等しく、6cmだと見て取れる。

柱の体積は「(底面積) × (高さ)」で求められるので、底面の円の面積の公式「(半径) × (半径) × (円周率)」と組み合わせて活用すると、以下のような式が立てられる。

(3 × 3 × π) × 6 = 9π × 6 = 54π　したがって、54π cm³　とわかる。

１−８：次のデータは、山下さんが釣り堀で釣った11匹の魚の重さを軽い方から順に並べたものです。このデータの四分位範囲は何 g ですか。

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
103 108 112 121 123 125 128 134 139 147 150　(単位：g)

解答 ： 27

解説 ： 四分位範囲は、データを小さい順に並べたときに、第1四分位数から第3四分位数までの範囲のことである。

まずは、問題において並べられたデータを使って、第1四分位数と第3四分位数を求める。

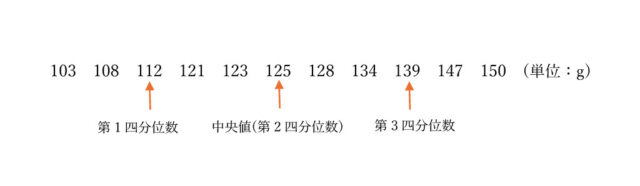
第1四分位数は112、第3四分位数は139とわかるので、139 – 112 = 27　よって、答えは　27。

■大問２

２−１：n を整数とします。45² – n² / 7　が自然数となるような n のうち、最も大きい n の値を求めなさい。

解答 ： 39

解説 ： 45² – n² / 7 について、分子の 45² – n² は因数分解することができる。「x² – a² = (x ₊ a)(x – a)」の公式を使って、45² – n² / 7 = (45 ₊ n)(45 – n) / 7　と変形できる。


(45 ₊ n)(45 – n) / 7　が自然数になるためには、nについては、0＜n＜45 である必要がある。同時に、(45 ₊ n) と (45 – n) のどちらかが7の倍数でなければならない。この2つの条件に当てはまるような n を考える。
・(45 ₊ n)が7の倍数になるのは、n = 4，11，18，25，32，39　のときである。
・(45 – n)が7の倍数になるのは、n = 3，10，17，24，31，38　のときとわかる。

したがって、45² – n² / 7　が自然数となるような n のうち、最も大きい n の値は、39である。よって、答えは　39。

２−２：次の図のように、点Ａ、B、C、D、E、F、G、Hを頂点とする直方体があり、AB = 4cm、AD = 6cm、AE = 3cm です。辺ADの中点をI、辺EFの中点をJとし、点Cと点I、点Jと点Cをそれぞれ結びます。このとき、△CIJの周の長さは何cmですか。

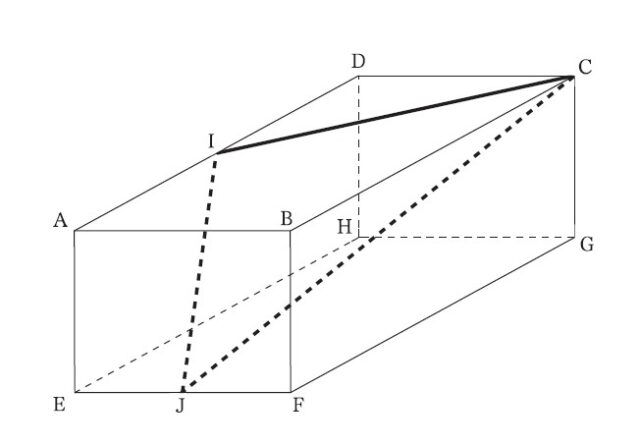
解答 ： (12 ₊ √22)

解説 ： まず、問題文からわかることを図に書き込んで整理する。


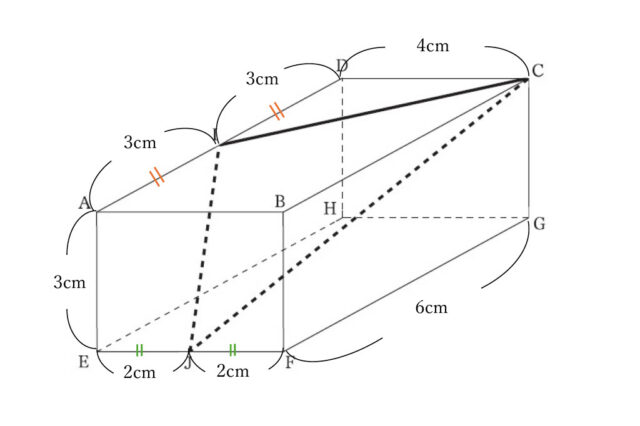
△CIJの周の長さは、辺IJと辺ICと辺CJの長さを足し合わせたものである。よって、3つの辺の、それぞれの長さを求める。


・辺IJについて。

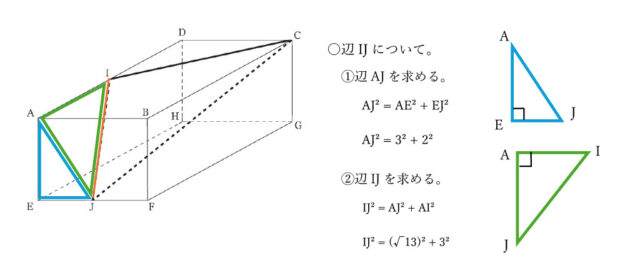
　辺IJは△AIJの1辺なので、辺AI、AJの2つの辺の長さが分かれば、三平方の定理を使って辺IJの長さを求めることができる。この2つの辺のうち辺AJの長さはわからないので、△AEJにおいて三平方の定理で求める。
AJ² = AE² + EJ²　→　AJ² = 3² + 2²　→　AJ² = 9 + 4　→　AJ² = 13　AJ＞0より、AJ = √13。
　同様に、△AIJにおいて三平方の定理を活用して、IJ² = AJ² + AI²　→　IJ² = (√13)² + 3²　→　IJ² = 13 + 9　→　IJ² = 22　IJ＞0なので、IJ = √22　と求められる。

・辺ICについて。

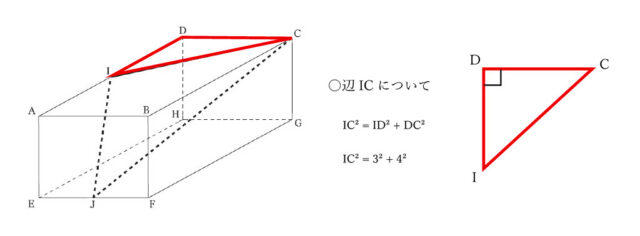
　辺ICは△IDCの1辺なので、辺IJのときと同様に、IC² = ID² + DC²　→　IC² = 3² + 4²　→　IC² = 9 + 16　→　IC² = 25　IC＞0より、IC=5　とわかる。

・辺CJについて。

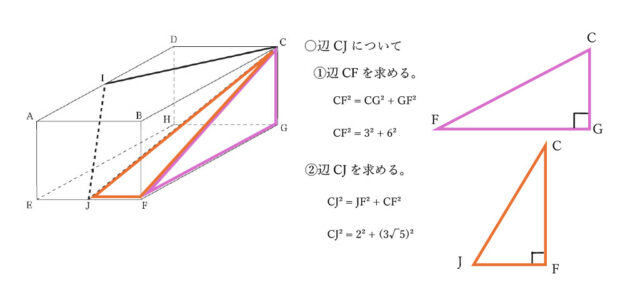
　辺CJは△CJFの1辺で、そのうち辺CFの長さが分かれば、三平方の定理を使って辺CJの長さを求めることができる。辺CFは△CFGの1辺なので、やはり三平方の定理で求める。
CF² = CG² + GF²　→　CF² = 3² + 6²　→　CF² = 9 + 36　→　CF² = 45　CF＞0より、CF = 3√5。△CJFにおいて三平方の定理を活用して、CJ² = JF² + CF²　→　CJ² = 2² + (3√5)²　→　CJ² = 4 + 45　→　CJ² = 49　CJ＞0なので、CJ = 7　と求められる。

以上より、△CIJの周の長さはIJ + IC + CJ = √22 + 5 + 7 = 12 + √22　とわかる。

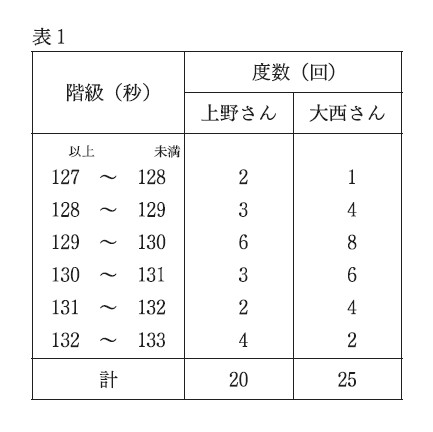
２−３：上野さんと大西さんは、ある学校の陸上部に所属しています。次の表1は、夏休みの期間に計測した、上野さんの800m走の20回分の記録と大西さんの800m走の25回分の記録を度数分布表に表したものです。


夏休み後に行われる陸上競技大会の種目には、800m走があり、出場する選手として、上野さんか大西さんのどちらか1人を選ぶことになりました。他の部員が、過去のその大会における800m走の決勝の記録をいくつか調べてみると、記録は全て、130秒未満でした。そこで、次の【選考方法】で、出場する選手を選ぶことにしました。

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
【選考方法】
夏休みの期間に計測した800m走の記録において、130秒未満の累積相対度数の大きい方の選手を、夏休み後に行われる陸上競技大会の800m走に出場する選手とする。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・

【選考方法】に基づくと、次の理由で出場する選手が選ばれます。

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
表1から、130秒未満の累積相対度数は、上野さんが[ ア ]、大西さんが[ イ ]であることを読み取ることができ、[ ウ ]の累積相対度数の方が大きいので、[ ウ ]が夏休み後に行われる陸上競技大会の800m走に出場する選手として選ばれる。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・

文中の[ ア ]・[ イ ]に当てはまる累積相対度数をそれぞれ求めなさい。ただし、累積相対度数は小数で表しなさい。
また、[ ウ ]に当てはまるものを、次の①・②の中から選び、その番号を書きなさい。なお、2か所の[ ウ ]には同じものが入ります。

① 上野さん　② 大西さん

解答 ： ア 0.55　イ 0.52　ウ ①

解説 ： まずは、上野さんと大西さんそれぞれの、130秒未満の累積相対度数を求める。
・上野さんの130秒未満の累積相対度数
　(1 + 4 + 8) ÷ 25 = 13 ÷ 25 = 0.52　
・大西さんの130秒未満の累積相対度数
　(2 + 3 + 6) ÷ 20 = 11 ÷ 20 = 0.55
よって、[ ア ]は0.52、[ イ ]は0.55が答えとなる。

また【選考方法】を読むと、「130秒未満の累積相対度数の大きい方の選手を、夏休み後に行われる陸上競技大会の800m走に出場する選手とする」と書かれている。したがって、累積相対度数の値の大きい大西さんの方が選手として選ばれると考えられ、[ ウ ]には②が適当である。

■大問３

ある会社では、年1回、家族向けのイベントを開催しています。そのイベントではこれまで、当日券の販売は行っていませんでしたが、来場者アンケートに、「前売り券だけではなく、当日券も販売してほしい。」という要望が多数あったことから、今年のイベントでは当日券も販売しました。
次の表1は、今年のイベントにおける、大人と子どもそれぞれ1人当たりの入場券(前売り券、当日券)の金額を表したものです。


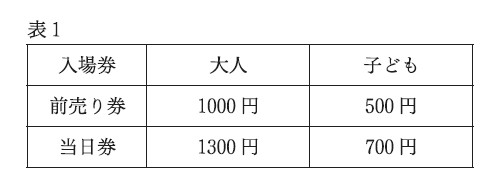
今年のイベントでは、購入された大人の入場券のうち、前売り券の割合は70％であり、購入された子どもの入場券のうち、前売り券の割合は60％であり、大人の入場券と子どもの入場券の売り上げの合計は 554100円でした。仮に、今年のイベントで購入された、大人の入場券と子どもの入場券が全て前売り券であった場合、入場券の売り上げの合計は 500000円となります。

今年のイベントで購入された、大人の入場券の枚数と子どもの入場券の枚数をそれぞれ求めなさい。ただし、入場券の枚数は、前売り券の枚数と当日券の枚数を合計した枚数です。なお、答えを求める過程も分かるように書きなさい。

解答 ：今年のイベントで購入された、大人の入場券の枚数をx枚、子どもの入場券の枚数をy枚とすると、 大人の入場券の売り上げ
　1000 × 70/100x + 1300 × 30/100x = 700x + 390x = 1090x (円)
子どもの入場券の売り上げ
　500 × 60/100y + 700 × 40/100y = 300y + 280y = 580y (円)

入場券の売り上げの合計から
　1090x + 580y = 554100　…①
入場券が全て前売り券であった場合の売り上げの合計から
　1000x + 500y = 500000　…②

①、②を連立方程式として解くと、 x = 370、y = 260。
x = 370、y = 260 は問題に適している。

よって、大人の入場券の枚数は370枚，子どもの入場券の枚数は260枚。

解説 ：問題文中に書かれているポイントは、以下のような表にまとめられる。


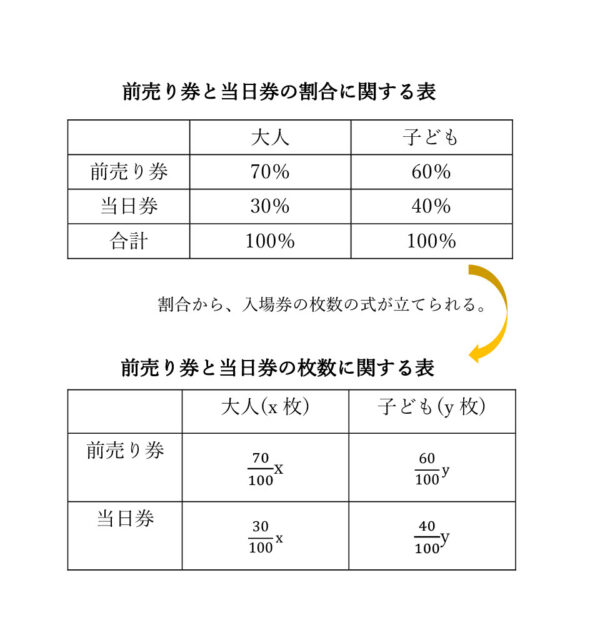
今年のイベントで購入された、大人の入場券の枚数をx枚、子どもの入場券の枚数をy枚とおく。すると、今年の大人と子ども、それぞれの売り上げは以下のように求められる。

・大人の入場券の売り上げ
　1000円 × 70/100x + 1300円 × 30/100x = 700x + 390x = 1090x 円
・子どもの入場券の売り上げ
　500円 × 60/100y + 700円 × 40/100y = 300y + 280y = 580y 円

次に、問題文より、「大人の入場券と子どもの入場券の売り上げの合計は 554100円」なので、1090x + 580y = 554100 という式が立てられる。
また、「仮に、今年のイベントで購入された、大人の入場券と子どもの入場券が全て前売り券であった場合、入場券の売り上げの合計は 500000円」とも書かれているので、ここから、1000x + 500y = 500000 という式も作ることができる。

この2つの式で以下のような連立方程式が考えられる。
1090x + 580y = 554100　…①
1000x + 500y = 500000　…②

この式を解くと、②より、10x + 5y = 5000　→　5y = -10x + 5000　→　y = -2x + 1000 と変形できる。
これを①の式に代入すると、
1090x + 580(-2x + 1000) = 554100　→　1090x – 1160x + 580000 = 554100　→　-70x = 54100 – 580000　→　-70x = -25900　→　-70x × (-1/70) = -25900 × (-1/70)　→　x = 370。
x = 370 を②の式に代入すると、370000 + 500y = 500000　→　500y = 500000 – 370000　→　500y = 130000　→　500y × 1/500 = 130000 × 1/500　→　y = 260。
以上より、 x = 370、y = 260とわかる。問題文より x＞0、y＞0なので、この答えは適していると考えられる。

したがって、今年のイベントで購入された、大人の入場券の枚数は370枚、子どもの入場券の枚数は260枚と求められる。

■大問４

４−１：次の図のように、関数 y = -x² のグラフ上に x座標が -2である点Aと x座標が3である点Bがあり、y軸上に点C(0, 1)があります。また、点Cを通り直線ABに平行な直線上を x＞0 の範囲で動く点Dがあります。


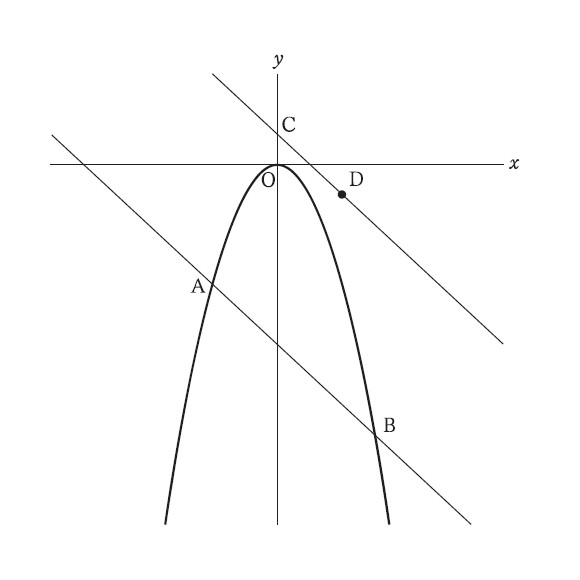
次の(1)、(2)に答えなさい。

関数y = -x² のグラフ上の点で、y座標が、点Aのy座標と等しい点をEとします。点Eの座標を求めなさい。ただし、点Eは点Aと異なる点です。

解答 ：(2, -4)

解説 ： まずは、問題文の内容から求められることを整理する。
点Aはy = -x² のグラフ上にあり、x座標が -2の点なので、この関数の式に代入して、y = -(-2)²　→　y = -4　よって、点Aの座標は(-2, -4)と求められる。
同様に点Bの座標も、x = 3 をy = -x² に代入して、y = -3²　→　y = -9。
したがって、点Bの座標は(3, -9)とわかる。


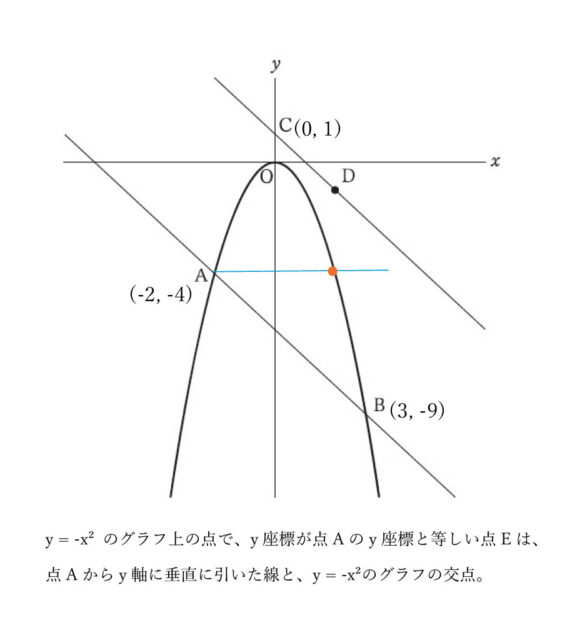
この問題で求めたいのは、y = -x² のグラフ上の点で、y座標が点Aのy座標と等しい点Eの座標である。
よって、先に求めた点Aの座標より、点Eのy座標は-4だとわかる。
これをy = -x² に代入すると、-4 = -x²　→　x² = 4　→　x = ±2。
点Aのx座標は-2なので、点Eのx座標が2だとわかる。
したがって、点Eの座標は(2, -4) と求められる。

４−２：四角形CABDの面積が25となるとき、点Ｄのx座標を求めなさい。

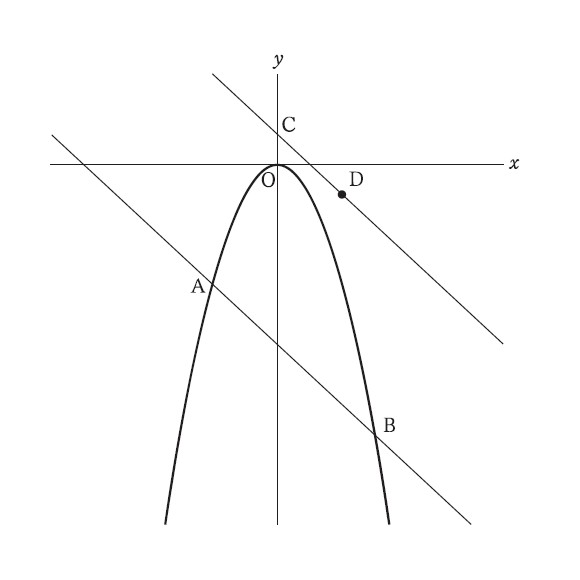
解答 ： 15/7

解説 ： 四角形CABDについて、CBの対角線で分けると、△CABと△CDBの面積を足し合わせたものだと考えられる。


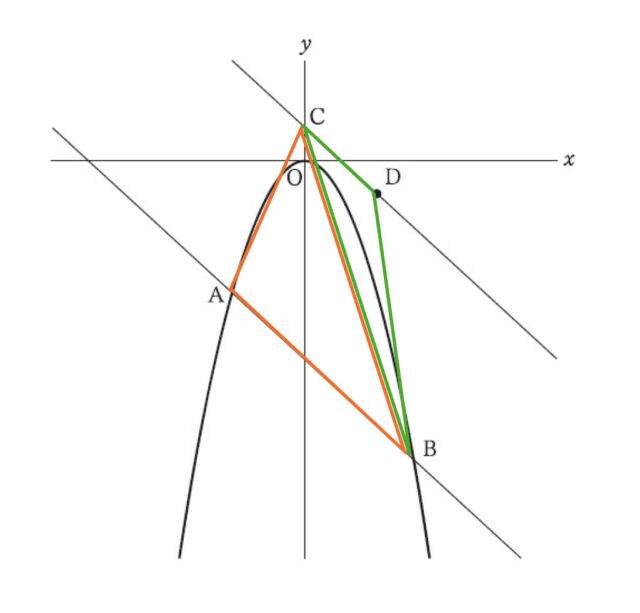
まず、△CABの面積を求める。直線ABとy軸との交点を点Pとおく。

この点Pはy軸と直線ABの交点であり、且つ直線ABの切片でもある。
直線ABの式をy = ax + b とおくと、点A、Bの座標を代入して、連立方程式を作ることができる。
-4 = -2a + b　…①
-9 = 3a + b　…②
①の式は、b = 2a – 4　と変形でき、これを②に代入して、-9 = 3a + (2a – 4)　→　-9 = 3a + 2a – 4　→　-9 = 5a – 4　→　5a = -5　→　a = -1。これを、先に変形した①の式に代入して、b = 2 × (-1) – 4　→　b = -2 – 4　→　b = -6　よって、直線ABの式は、y = -x – 6 と求められ、点Pの座標は(0, -6)とわかる。

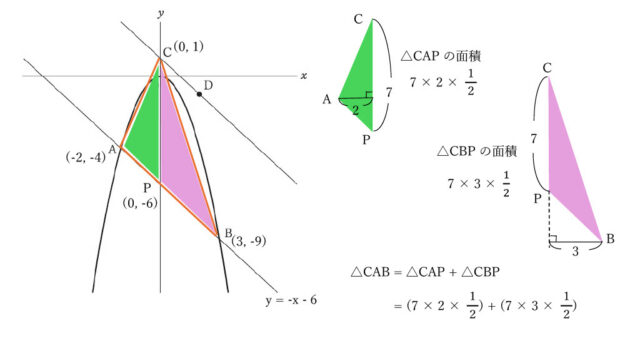
△CABは、y軸で△CAPと△CBPに分割でき、それぞれの面積を足したものだと考えられる。
この際、△CAPと△CBPの共通な底辺を、CPの部分と捉えると底辺は7とわかる。その場合、△CAPの高さはy軸から点Aまでの長さであるため2とわかり、同様に△CBPの高さは3である。
したがって、△CAB = △CAP + △CBP = (7 × 2 × 1/2) + (7 × 3 × 1/2) = (14 + 21) / 2 = 35/2　と求められる。

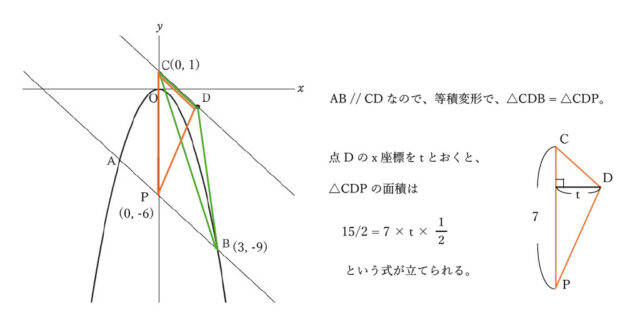
四角形CABDの面積は、△CABと△CDBの面積を足し合わせたものなので、25 = △CAB + △CDB　→　25 = 35/2 + △CDB　→　△CDB = 25 – 35/2　→　△CDB = 15/2　とわかる。
ここで△CDBについてより詳しく見ると、AB // CD等積変形の考え方で△CDB = △CDP = 15/2 と言える。点Dのx座標をtとおくと、△CDP = 15/2 = 7 × t ×1/2　→　7/2t = 15/2　→　7/2t × 2/7 = 15/2 × 2/7　→　t = 15/7。　以上より、点Dのx座標は15/7 と求められる。

■大問５

５−１：数学の授業で、中川さんはコンピュータを用いて、次の【手順】で図1のような図形をかき、その図形を考察することにしました。


・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
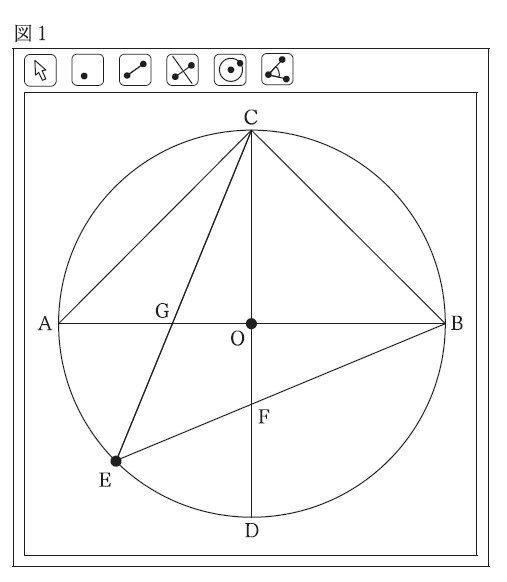
【手順】
[1] 線分ABをかき、ABの中点をOとする。
[2] 点Oを中心として、OAを半径とする円Oをかく。
[3] 線分ABの垂直二等分線を引き、円Oとの交点をそれぞれC、Dとする。
[4] 弧AD上に弧AE = 弧ED となる点Eをとる。
[5] 点Bと点Eを結んだ線分BEと線分ODとの交点をFとする。
[6] 点Cと点Eを結んだ線分CEと線分OAとの交点をGとする。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・

次の(1)・(2)に答えなさい。

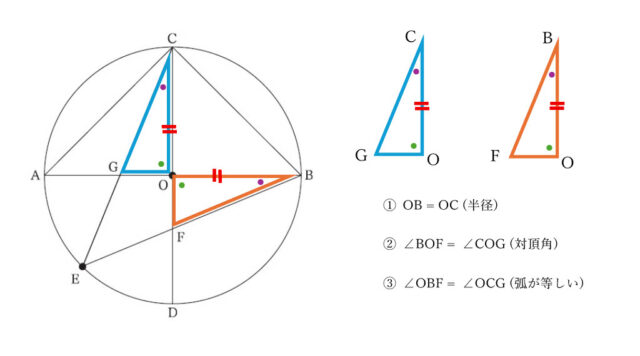
中川さんは、図1から、△OFBと△OGCが合同であると予想しました。そして、次のように△OFBと△OGCが合同であることを証明しました。

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
【証明】
△OFBと△OGCにおいて
OBとOCは、円Oの半径であるから、OB = OC　…①
対頂角は等しいから、∠BOF = ∠[ ア ]　…②
弧AE = 弧EDであるから、∠OBF = ∠[ イ ]　…③
①、②、③より、[　ウ　]がそれぞれ等しいから
　△OFB ≡ △OGC
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・

【証明】の[ ア ]・[ イ ]には、当てはまる文字をそれぞれ書き、[　ウ　]には、当てはまる言葉を書き、証明を完成させなさい。

解答 ： ア COG　イ OCG　ウ 1組の辺とその両端の角

解説 ： △OFBと△OGCについて、以下の図のように整理できる。

・[ ア ]について。
　△OGCの内角で、∠BOFと対頂角の関係になっている角を当てはめればいいので、∠COGが適当である。

・[ イ ]について。

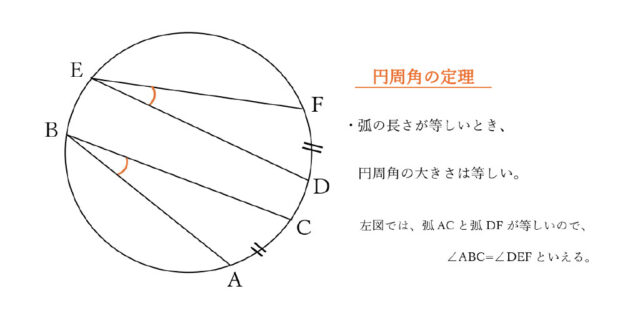
　弧AE = 弧EDから分かることで、且つ[ イ ]と等しい角は∠OBFなので、ここでは円周角の定理を活用して等しい角を見つけたらよい。また、∠OBFは弧AEからなる円周角なので、[ イ ]に当てはまるのでは、△OGCの内角であり、弧EDの円周角だと考えられる。よって、[ イ ]には∠OCGが適当である。

・[ ウ ]について。
　①、②、③で揃えた要素から、[ ウ ]には「1組の辺とその両端の角」が等しいと書くのが適当である。

５−２：次に、中川さんはコンピュータを用いて、次の図2のように、図1にある、5点A、B、O、C、Dを固定して、点Eを、点Aと点Dを除く弧AD上で動かしたとき、何か成り立つことがあるのではないかと考え、調べることにしました。そこで、コンピュータで角の大きさを表示できる機能を用いて、点Eのいくつかの位置における、∠OFBの大きさと∠OGCの大きさをそれぞれ調べ、下の表1にまとめました。



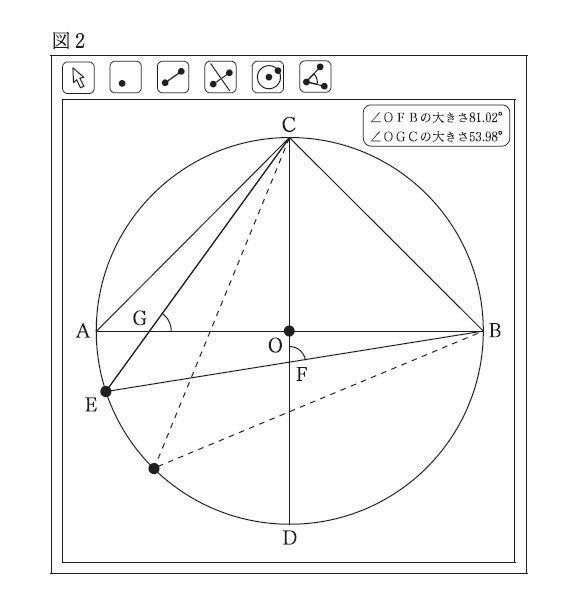
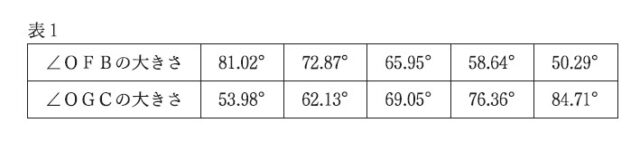
中川さんは、表1から、次のことを予想しました。

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
【予想】
点Eが、点Aと点Dを除く弧ADのどの位置にあっても、∠OFBの大きさと∠OGCの大きさの和は135°である。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・

【予想】が成り立つことを、∠OFBの大きさを∠a、∠OGCの大きさを∠bとして、∠a、∠bを使った式を用いて説明しなさい。なお、弧ADは、点Bをふくまない方の弧を指します。

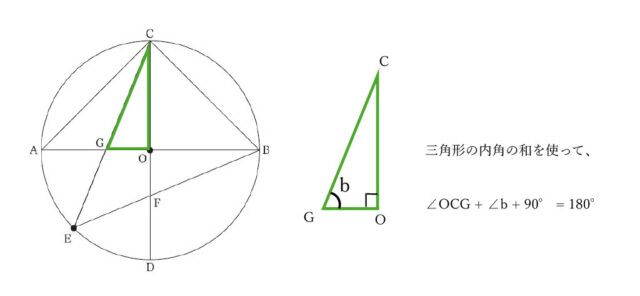
解答 ：
AB⊥CDであるから
　∠BOC = 90°
弧BCに対する円周角∠BECの大きさは、弧BCに対する中心角∠BOCの大きさの半分であるから
　∠BEC = 45°
∠OFBは△CEFの外角であるから
　∠a = ∠OCG + 45°　　…①
AB⊥CDであるから
　∠COG = 90°
△OGCの内角の和は180°であるから
　∠OCG + ∠b + 90° = 180°
　∠b = 90° – ∠OCG　　…②
①、②より
　∠a + ∠b = (∠OCG + 45°) + (90° – ∠OCG)
　　　　　 = 135°
したがって、点Eが、点Aと点Dを除く弧AD上のどの位置にあっても、∠OFBの大きさと∠OGCの大きさの和は135°である。

解説 ：
※「答えを求める過程も分かるように書きなさい。」という指示の問題なので、以下の解説は解答をもう少し詳しく説明したものになっています。そのため、重複する部分も多いです。

【手順】の[3]より、線分CDは線分ABの垂直二等分線なので、AB⊥CDであり、∠BOC = 90°。
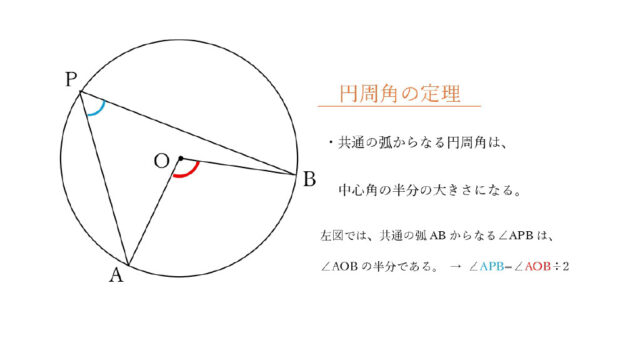
円周角の定理より、弧BCに対する円周角∠BECの大きさは、弧BCに対する中心角∠BOCの大きさの半分なので、∠BEC = 45°。
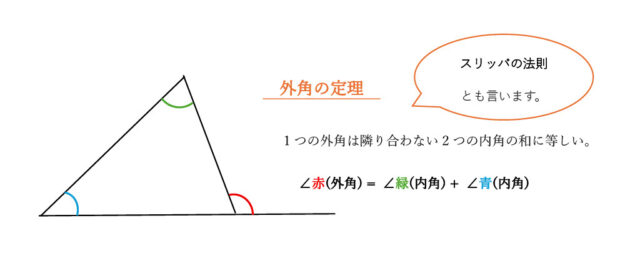
∠OFBは△CEFの外角なので、外角の定理を活用して、
　∠a = ∠ECF + ∠CEF　→よって、∠a = ∠OCG + 45°　…①　




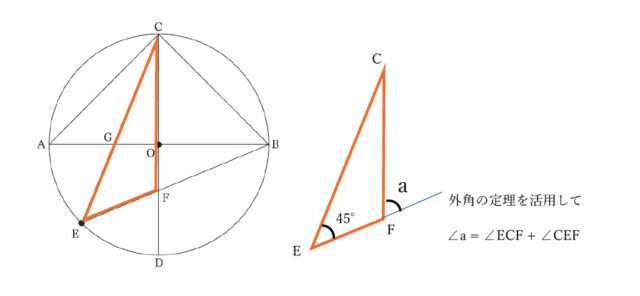
次に、△OGCに着目する。
AB⊥CDなので、∠COG = 90°。
△OGCの内角の和は180°なので、
　∠OCG + ∠b + ∠COG = 180°　→　∠OCG + ∠b + 90° = 180°　→　∠b = 180° – ∠OCG – 90° 　→　∠b = 90° – ∠OCG　…②
①、②より、
　∠a + ∠b = (∠OCG + 45°) + (90° – ∠OCG) = ∠OCG – ∠OCG + 45° + 90° = 135°
したがって、点Eが、点Aと点Dを除く弧AD上のどの位置にあっても、∠OFBと∠OGCの大きさの和は135°である。

■大問６

６−１：右の図1のように、1、2、3、4、5 の数が1つずつ書かれた玉が5個入った袋があります。また、片面が白色、もう片面が黒色の5枚のカードがあり、机の上に、図2のように、白色の面が上になって横一列に並んでいます。袋の中から取り出した玉に書かれている数を利用して、カードを裏返す、【操作P】および【操作Q】についてそれぞれ考えます。




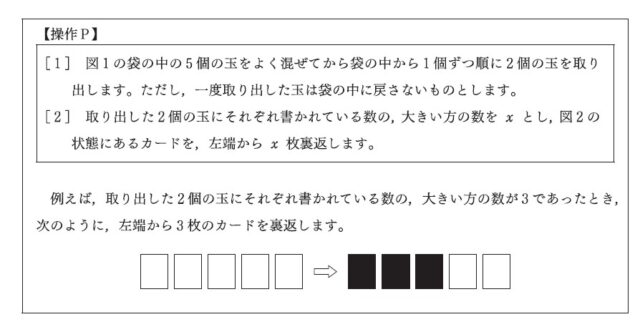
【操作P】を1回だけ行うとき、5枚のカードにおいて、白色の面が上であるカードが1枚、黒色の面が上であるカードが4枚となる確率を求めなさい。

解答 ： 3/10

解説 ： 【操作P】の[1]より、「袋の中から1個ずつ順に2個の玉を取り出す」こと、「一度取り出した玉は袋の中に戻さない」ことがわかり、この操作を1回行うので、ここから樹形図をかくことができる。樹形図より、玉の取り出し方は全部で20通りとわかる。


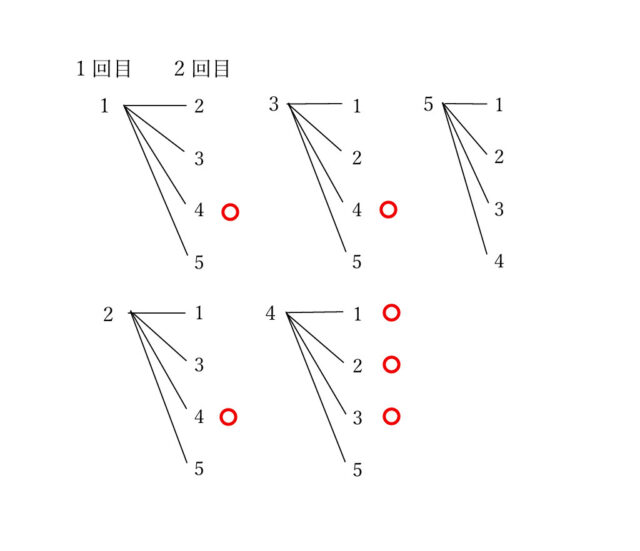
次に、【操作P】の[2]の「取り出した2個の玉にそれぞれ書かれている数の、大きい方の数をxとし、図2の状態にあるカードを、左端からx枚裏返します」という部分に着目する。ここから、白色の面が上であるカードが1枚、黒色の面が上であるカードが4枚となるのは、取り出した2個の玉のうち大きい方の数字が4のときだとわかる。樹形図のうち、このような場合は(1, 4)、(2, 4)、(3, 4)、(4, 1)、(4, 2)、(4, 3)の4通りである。

したがって、【操作P】を1回行って、白色の面が上であるカードが1枚、黒色の面が上であるカードが4枚となる確率は、6/20 = 3/10　よって、答えは　3/10　とわかる。

６−２：【操作Q】を1回だけ行うとき、5枚のカードにおいて、白色の面が上であるカードが1枚、黒色の面が上であるカードが4枚となる確率を求めなさい。

解答 ： 8/25

解説 ： 【操作Q】の[1]より、初めに袋から1個玉を取り出し、その玉を戻して混ぜて、もう1個玉を取り出すことがわかる。ここから、以下のような樹形図を作ることができる。ここから、玉の取り出し方は、全部で25通りだと求められる。


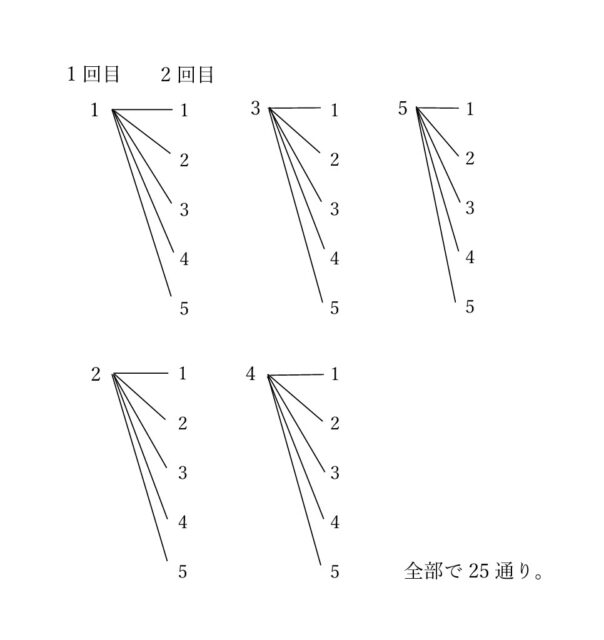
【操作Q】の[2]より、「1回目に取り出した玉に書かれている数をa、2回目に取り出した玉に書かれている数をbとし、図2の状態にあるカードを、最初に左端からa枚裏返し、次に右端からb枚裏返します」という記載に着目する。今回求めたいのは、白色の面が上であるカードが1枚、黒色の面が上であるカードが4枚となる場合なので、以下のような図で整理できる。該当する1回目と2回目の玉の数字の組み合わせは、(5, 4)、(1, 3)、(2, 4)、(2, 2)、(3, 3)、(3, 1)、(4, 2)、(5, 1)の8通りあることがわかる。


したがって、【操作Q】を1回行って、白色の面が上であるカードが1枚、黒色の面が上であるカードが4枚となる確率は、8/25　とわかる。